Фаза колебаний
Фаза колебаний — это аргумент периодически изменяющейся функции, описывающей колебательный или волновой процесс.
Для гармонических колебаний
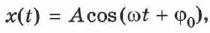
где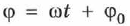 
— фаза колебания, 
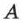— амплитуда, 
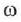— круговая частота, 
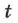— время, 
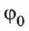— начальная (фиксированная) фаза колебания: в момент времени 
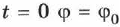. Фаза выражается в радианах.
Фаза гармонического колебания при постоянной амплитуде определяет не только координату колеблющегося тела в любой момент времени, но и скорость и ускорение, которые тоже изменяются по гармоническому закону (скорость и ускорение гармонических колебаний — это первая и вторая производные по времени функции (1.58), которые, как известно, снова дают синус и косинус). Поэтому можно сказать, что фаза определяет при заданной амплитуде состояние колебательной системы в любой момент времени.
Два колебания с одинаковыми амплитудами и частотами могут отличаться друг от друга фазами. Так как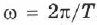 
, то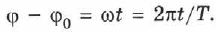 
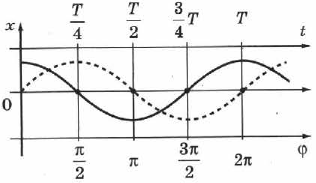
Отношение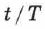 
показывает, какая часть периода прошла от момента начала колебаний. Любому значению времени, выраженному в долях периода, соответствует значение фазы, выраженной в радианах (рис. 57). Сплошная кривая на рис. 57 — это зависимость координаты от времени и одновременно от фазы колебаний (верхние и нижние значения на оси абсцисс соответственно) для точки, совершающей гармонические колебания по закону:
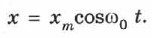
Здесь начальная фаза равна нулю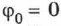 
. В начальный момент времени амплитуда максимальна. Это соответствует случаю колебаний тела, прикреплённого к пружине (или маятника), которое в начальный момент времени отвели от положения равновесия и отпустили. Описание колебаний, начинающихся из положения равновесия (например, при кратковременном толчке покоящегося шарика), удобнее вести с помощью функции синуса:
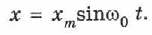
Как известно,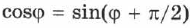 
, поэтому колебания, описываемые уравнениями (1.59) и (1.60), отличаются друг от друга только фазами. Разность фаз, или сдвиг фаз, составляет 
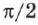. Чтобы определить сдвиг фаз, нужно колеблющуюся величину выразить через одну и ту же тригонометрическую функцию — косинус или синус. Пунктирная кривая на рис. 57 (это график уравнения (1.60)) сдвинута относительно сплошной на 
.
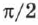Эта лекция взята со страницы лекций по всем темам предмета физика:
Возможно эти страницы вам будут полезны:
| Свободные колебания в физике |
| Динамика свободных колебаний в физике |
| Затухающие колебания в физике |
| Вынужденные колебания в физике |
