Эвристический алгоритм решения задачи синтеза сети связи

Эвристический алгоритм решения задачи синтеза сети связи

Как уже отмечалось, сетевые задачи большой размерности решают восновном приближенными эвристическими методами. Рассмотрим один из эвристических методов на примере задачи синтеза некоторой сети связи.

Одна из основных задач при разработке схемы сети связи — это определение наивыгоднейшей конфигурации и распределения каналов на сети. При этом могут решаться и другие задачи:

1) выбор типа линий связи (кабельные, радиорелейные, воздушные и т.п.) с соответствующими системами передачи;

2) последующее распределение стандартных каналов на сети.

Структура сети — ее топология — это совокупность пунктов

(узлов, станций и т.п.) и соединяющих их линий связи или каналов в их взаимном расположении. Она показывает потенциальные возможности обеспечения связью отдельных пунктов этой сети.

Экономически оптимальный выбор сетки линий, их емкостей и плана распределения каналов при заданном наборе пунктов сети называют задачей оптимального синтеза структуры сети. Ее решение существенно зависит от того, насколько тщательно отобраны допустимые направления.

В качестве основных критериев оптимальности построения сети обычно рассматривают объем капитальных затрат, расход кабельной продукции и т.д. Минимум расхода кабельной продукции обеспечивается при минимуме общей протяженности трасс кабельных и радиорелейных линий связи. Иногда в качестве критерия оптимальности может рассматриваться и объем строительно-монтажных работ.

Реальная сеть должна отвечать одновременно в той или иной мере всем критериям оптимальности, т.е. задача определения наивыгоднейшей конфигурации и распределения каналов сети является многокритериальной. Но в связи со сложностью решения многокритериальных задач обычно в качестве оптимальной принимают сеть, отвечающую одному, какому-либо заранее заданному критерию оптимальности. Очевидно, что сеть в общем случае будет различной в зависимости от используемого критерия оптимальности.

Рассмотрим задачу синтеза сети при следующих требованиях:

1. Каждый пункт сети должен иметь два независимых пути к центральному узлу (ЦУ) (прямой и обходной). Прямой путь должен обеспечивать передачу по 70-75% каналов от их расчетного числа, а обходной путь — соответственно по 25-30% каналов. Это соотношение может измениться, а поэтому должно задаваться на входе задачи.
2. Должен быть путь, соединяющий каждый пункт сети с дополнительным узлом связи (ДУ), не совпадающим с ЦУ. На некоторых участках этот путь может совпадать с прямым и обходным путями.

В сетях связи накладывают дополнительные требования:

1. На линиях связи пункт — ЦУ число транзитов по высокой частоте (ВЧ) должно быть не более двух в случае применения аналоговых систем передачи.
2. Суммарная емкость (число каналов) на любом участке зоновой сети должна быть кратна 12 для аналоговых систем передачи и 30 для цифровых систем.
3. Иногда требуется предусмогреть возможность того, чтобы через некоторые пункты проходило минимальное число путей. Эти пункты отмечают в исходных данных.

Задача синтеза структуры сети может быть наиболее адекватно представлена (в силу нелинейного ступенчатого изменения целевых функций, в частности функции стоимости линии связи) как задача целочисленного нелинейного программирования в различных формах.

Рассмотрим задачу выбора оптимального варианта построения сети с двумя независимыми путями к единственному узлу (центральному), к которому передается информация со всех других узлов сети. В качестве целевой функции выступает функция стоимости сети.

Задан неориентированный граф (сеть) 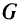с 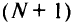вершинами. Все вершины, кроме 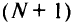-й, являются источниками информации. Вершина 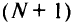является стоком (центральным узлом). Путем 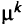от вершины к к стоку 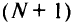будем называть последовательность вершин 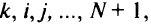, через которые проходит данный путь. Для каждой вершины 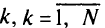необходимо выбрать два пути к стоку,

не имеющих общих вершин, кроме 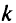и 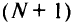. Заданы потоки информации 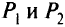, которые требуется передать от вершины к к стоку соответственно по первому и второму путям. Дугам графа 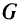при-писаны веса, равные их длинам. Для общности рассмотрения заданный граф 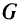дополним до полного дугами с достаточно большим весом вместо отсутствующих.

Цель задачи — выбор топологии сети и маршрутов передачи информации на ней, минимизирующих общую стоимость сети. Общая стоимость сети определяется как сумма стоимостей входящих в нее дуг. Стоимость дуги 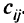является функцией от длины дуги 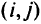и суммарного потока информации на ней — суммы потоков от вершины 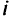к вершине 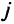и от вершины 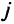к вершине 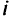. Конкретный вид функции стоимости не имеет принципиального значения и может быть произвольным. В дальнейшем предполагается, что функция стоимости возрастает с ростом расстояния и не убывает с ростом суммарного потока. Известно, что оптимальная сеть при различных минимизируемых величинах может быть получена по одному и тому же алгоритму при соответствующем выборе величины .

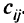Введем следующие обозначения:

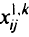— булева переменная, равная 1, если вершина 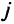непосредственно следует за вершиной 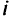на первом пути 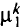от вершины к к стоку, и 0 в противном случае

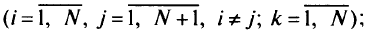
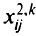— булева переменная, равная 1, если вершина 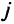непосредственно следует за вершиной 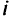на втором пути от вершины 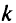к стоку, и 0 в противном случае

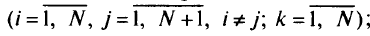
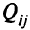— суммарный поток информации на дуге 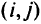, определяемый по формуле

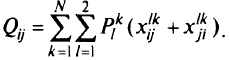
Тогда рассматриваемую задачу можно сформулировать следующим образом. Необходимо найти значения булевых переменных 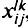, минимизирующих общую стоимость сети:

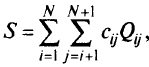
где 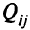— вычисляют по формуле (5.15) при ограничениях:

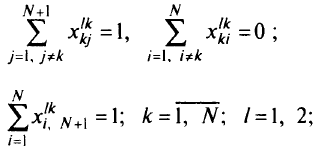
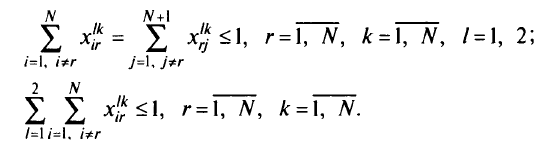
Ограничение (5.17) означает, что началом как первого, так и второго пути от вершины 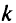к стоку должна быть вершина 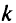. Ограничение (5.18) предопределяет, что все пути должны оканчиваться в вершине 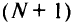. Ограничение (5.19) указывает на условия сохранения потока (равенство) и на запрет на петли в путях от вершины к стоку (неравенство). Заметим, что если функция стоимости монотонно возрастает с ростом суммарного потока, то ограничение (5.19) в виде неравенства можно опустить. Ограничения (5.20) реализуют условие непересечения первого и второго путей от каждой вершины к стоку по вершинам.

Как видно, данная математическая постановка предполагает наличие 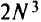булевых переменных и 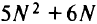ограничений, что в практически интересных случаях 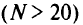не позволяет рассчитывать на точное решение. Исключение составляет случай, когда функция стоимости линейна относительно суммарного потока. Поскольку целевая функция (5.16) становится линейной по переменным 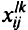, это позволяет осуществить декомпозицию исходной задачи на 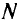независимых задач булевого программирования с целевой функцией

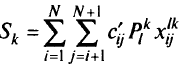
и ограничениями (5.17)—(5.20) при фиксированных значениях 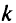, , 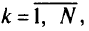где 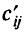— стоимость единицы потока по дуге .

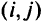Последняя задача (при фиксированном 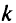) может быть сформулирована достаточно просто: найти два пути от вершины к к вершине 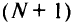, не имеющих общих вершин, кроме 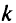и 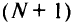, и обеспечивающих минимум суммарной стоимости путей. При этом стоимость пути равна стоимости входящих в него дуг, а стоимость дуги 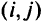равна 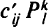для 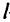-го пути .

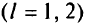Математическую постановку задачи с двумя независимыми путями к центральному узлу и одним путем к ДУ (дополнительному узлу) можно записать в следующем виде.

Пусть вершина с номером 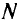является ДУ. Через 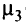будем обозначать путь от к вершины к ДУ

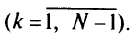
При этом

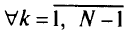
путь 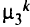не должен содержать вершину 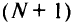. Пусть 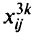— булева переменная, равная 1,если вершина связана с вершиной на пути 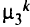от вершины к к ДУ, и 0 в противном случае. Через 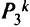будем обозначать требуемые величины потоков информации от вершины

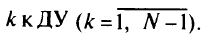
Тогда, придерживаясь прежних обозначений, суммарный поток на дуге 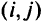определяем по формуле

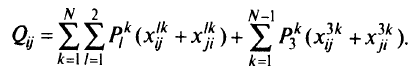
Для дуг

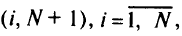
суммарный поток, как и раньше, вычисляют по формуле (5.15).

Рассматриваемую задачу можно сформулировать следующим образом. Найти значения булевых переменных

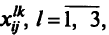
минимизирующих общую стоимость сети, вычисляемую по формуле (5.16) при ограничениях (5.17) — (5.20) и ограничениях

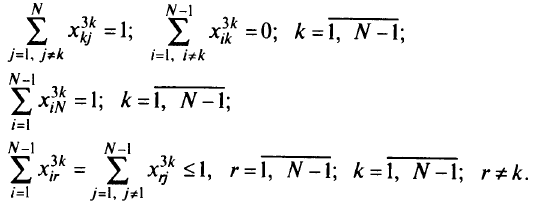
Офаничения (5.23)—(5.25) аналогичны офаничениям (5.17)-(5.19). Аналог офаничения (5.20) отсутствует, поскольку к ДУ необходимо построить только один путь от каждой вершины.

Как легко видеть, требование наличия путей к ДУ увеличивает число переменных на 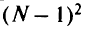и число ограничений на .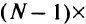

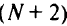Но, как и ранее, в случае, когда функция зависимости стоимости дуги от величины суммарного потока линейна, задача распадается на две независимые задачи:

1) определение двух непересекающихся путей к центральному узлу;

2) определение путей к вершине N, имеющих минимальную суммарную стоимость.

Математическая постановка первой из этих задач уже рассматривалась, а вторая, как легко видеть, приводит к задаче построения кратчайших путей от каждой вершины к N-й.

В обеих постановках случайными величинами являются значения Pf, так как их получают в результате прогнозов и, в крайнем случае, задают в виде интервалов с соответствующими значениями вероятностей. Другой случайной величиной может быть доля информации, передаваемой по прямому (или обходному) пути.

Полученная нелинейная целочисленная задача может быть решена на современных ЭВМ лишь для сети малых размеров: число пунктов 10 при 20-30 допустимых трассах. Размеры реальных сетей, как правило, больше. Поэтому в некоторых работах проводят линеаризацию данной задачи. В результате задачу сводят к целочисленной линейной или просто к задаче линейного программирования. Но в этом случае для получаемого решения не гарантируется определенная степень приближения критерия затрат к минимуму.

Большая размерность описанных задач и стохастическая природа исходных данных приводит к необходимости разработки эвристических алгоритмов решения. Кроме того, сама специфика структуры сетевых задач позволяет находить более эффективные алгоритмы поиска решения, чем алгоритмы в точных методах решения.

В литературе описан ряд эвристических методов, учитывающих специфику поставленной задачи. Но в этих алгоритмах для решения задачи используют, хотя и в разной степени, дуги минимальной длины. Следовательно, они ориентированы в некоторой степени на сеть минимальной длины, что не всегда позволяет найти наилучший результат, тем более этот недостаток будет сказываться при построении коротких сетей, в которых расстояния между узлами малы, так как в этом случае стоимость сети в основном определяется стоимостью аппаратуры и мало зависит от длины трасс.

Алгоритм синтеза сети без ДУ. Алгоритм для решения общей задачи (5.15)—(5.20) состоит из трех этапов:

I — построение первых путей от всех вершин к стоку;

II — построение вторых путей от всех вершин к стоку;

III — улучшение сети, полученной на первых двух этапах.

На этапе I выполняются следующие шаги:

Шаг 1. Строят начальную звездообразную сеть, в которой каждая вершина напрямую, без промежуточных узлов, соединена со стоком, и подсчитывают стоимость такой сети согласно заданной функции стоимости. Если для какой-то вершины связь со стоком отсутствует в исходном графе, то стоимость такой несуществующей дуги полагают равной достаточно большому числу.

Шаг 2. Для каждой вершины к, путь от которой является радиальным путем

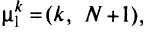
вычисляют экономию 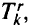которая будет получена при замене пути 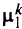на путь

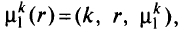
и равна разности их стоимостей. При этом промежуточная вершина пробегает по всем вершинам, инцидентным вершине к (т.е. связанным с вершиной к разрешенными дугами), и по пути 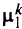. Пути от вершины до стока не содержат несуществующих дуг. Затем из всех экономий 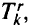выбирают максимальную.

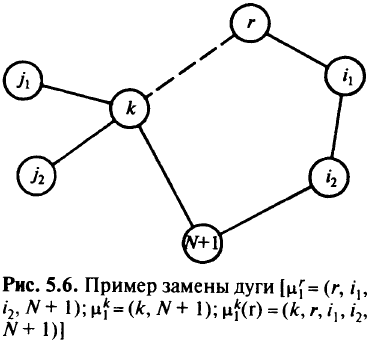
На рис. 5.6 приведен пример такой замены. Экономия достигается за счет ликвидации дуги 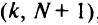, но при этом может увеличиться стоимость дуг пути .

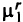ШагЗ. Выбирают максимальное значение 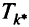из всех экономий 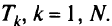. Если 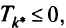то этап I считают завершенным.

Шаг4. Для выбранного осуществляют замену пути 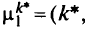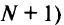на путь

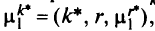
на котором достигалась максимальная экономия 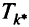. Осуществляют замену путей для всех вершин пути от которых проходили по дуге

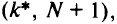
т.е. вместо пути

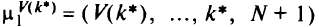
формируют новый путь

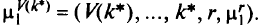
На рис. 5.6 такими вершинами являются вершины 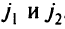. Новый путь для вершины 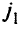, например, будет

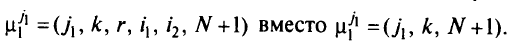
Шаг 5. Экономию 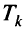полагают равной 0 для всех 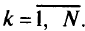. Переход к шагу 2.

Шаги 2—5 выполняют до тех пор, пока может быть достигнута экономия при замене какого-либо радиального пути на путь через промежуточную вершину. Пересчет экономии ^осуществляется после каждой замены радиального пути.

Поскольку каждый раз происходитуменьшение на единицу числа радиальных путей, то этап I конечен.

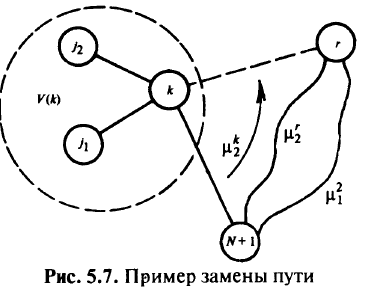
На этапе II осуществляют построение вторых путей от каждой вершины к стоку. Идея алгоритма на этапе II та же — замена радиального второго пути на путь через промежуточную вершину.

Шаг 1 аналогичен шагу 1 этапа I. Отличия лишь в том, что если первый путь от некоторой вершины после завершения этапа I оставался радиальным, то радиальный второй путь прокладывают по несуществующей второй дуге к стоку и его стоимость полагают вдвое большей, чем стоимость несуществующей дуги. Смысл этого в том, что такие пути выгоднее всего заменять, а значит, они будут заменены в первую очередь. Кроме того, при подсчете стоимости сети учитывают первые пути от всех вершин к стоку.

Шаг 2 аналогичен шагу 2 этапа I. Только теперь существует две возможности замены радиального второго пути от к-й вершины на путь через промежуточную вершину r, а именно:

новый путь идет от вершины к к вершине r, а затем либо по первому, либо по второму пути от вершины r к стоку (конечно, при этом второй путь должен быть реальным).

Обозначим через множество вершин, вторые пути которых проходят по дуге 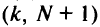, при этом 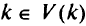. Тогда путь 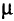можно заменить на путь 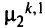или 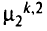только в том случае, если

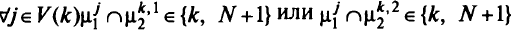
соответственно. Схематично вышесказанное показано на рис. 5.7.

Шаги 3—5 аналогичны шагам 1 этапа.

Шаги 2-5 выполняются до тех пор, пока замена какого-либо радиального пути на путь через промежуточную вершину может дать положительную экономию.

После выполнения I и II этапов мы получим сеть с размеченными на ней маршрутами первых и вторых путей от каждой вершины к стоку. Эта сеть с маршрутами удовлетворяет всем условиям задачи, т.е. является допустимой. Кроме того, она обладает следующими особенностями.

Каждая вершина имеет не менее двух инцидентных вершин сети, поскольку осушеств-

ляет два непересекающихся по вершинам, а следовательно, и по дугам пути. Инцидентными вершинами называют вершины, связанные разрешенными дугами.

• По каждой дуге сети 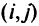согласно выбранным маршрутам обоих путей происходит передача информации либо только в одну сторону, например от вершины 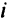к вершине 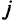, либо в обе стороны. В первом случае дугу 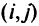ориентируем от 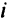к 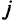, а во втором случае дуга 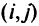будет ориентирована в обе стороны. После ориентации сети описанным образом получим, что каждая вершина сети имеет ровно две выходящих из нее дуги (кроме, конечно, стока). Входящих же дуг может быть произвольное число. Это следует из алгоритма замены радиального пути на путь через промежуточную вершину.
• Если же по дуге 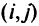от вершины 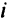к вершине 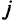идет поток информации 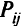, то в дальнейшем он полностью проходит по первому или второму пути от вершины 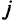к стоку. Этот факт также следует из алгоритмов I и И этапов.

Особенности сети, отмеченные в п. 2 и 3, облегчают реализацию III этапа.

Если после выполнения первых двух этапов каждая вершина сети имеет ровно две инцидентные вершины (кроме, разумеется, стока), то полученная сеть не будет обладать избыточностью.

В этом случае возможность улучшения сети заключается только в попытке заменить какой-либо радиальный первый путь. Если же некоторые вершины имеют более двух инцидентных вершин, то полученная сеть обладает известной избыточностью. На III этапе осуществляют попытку улучшить сеть с точки зрения ее обшей стоимости в обоих случаях.

Шаг I. Составляют множество дуг — претендентов на замену. В него включают все дуги 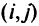, ориентированные лишь в одну сторону

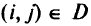Обозначим это множество через . Для каждой дуги составляют множество вершин 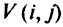пути от которых проходят по дуге 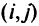, и множество путей 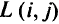(первые или вторые пути от вершин множества 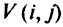, проходящие по дуге ).

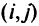Шаг 2. Для каждой дуги 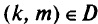(рис. 5.8) вычисляют экономию, которая может быть получена при замене дуги 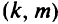на дугу 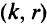с соответствующим изменением маршрутов первых или вторых путей для всех вершин 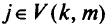на путь

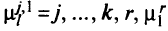
или путь

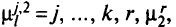
т.е. новый путь идет, как и раньше, до вершины к, а далее через вершину r и по первому или второму пути от вершины r к стоку. Такую замену можно осуществить лишь в том случае, когда:

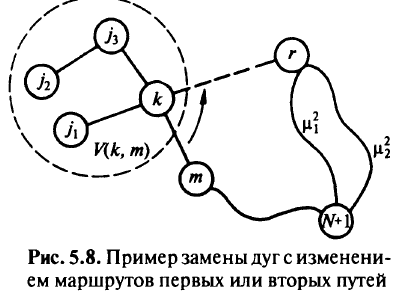
1) для любой вершины 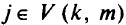другой путь не имеет общих вершин с 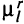, кроме 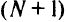-й;

2) сам путь 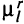не содержит вершин из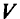 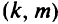, т.е.

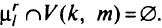
Экономии при этом достигают за счет ликвидации дуги 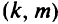, а также за счет уменьшения потока на 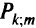для остальных дуг пути 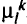Но при этом может произойти рост стоимости сети от включения в сеть дуги 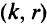или увеличения на 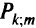потока на дуге 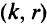и на дугах путе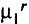й или .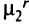

ШагЗ. Выбирают дугу 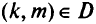и соответствующую вершину г, на которых достигается максимальная экономия. Если максимальная экономия положительна, то выполняют шаг 4, в противном случае — завершение III этапа.

Шаг 4. Осуществляют модификацию сети, маршрутов путей, множеств в соответствии с выбранными на шаге 3 дугой , вершиной r и путем от вершины r к стоку. После этого — переход к шагу 2.

После завершения III этапа работа эвристического алгоритма считается законченной.

Алгоритм синтеза сети с ДУ. Схема эвристического алгоритма для решения задачи (5.15)—(5.25) приведена на рис. 5.9.

На каждой итерации осуществляют последовательное выполнение описанных выше трех этапов эвристического ал горитма построения двух непересекающихся путей к центральному узлу, после чего осуществляют построение путей к ДУ с помощью III этапа эвристического алгоритма и проводят попытку уменьшить стоимость сети заменой некоторых маршрутов путей к центральному узлу с учетом новых путей к ДУ с помощью III этапа эвристического алгоритма. На каждой итерации (кроме первой) при построении первых и вторых путей к центральному узлу учитывают потоки информации, проходящие по сети согласно построенным на предыдущей итерации путям к ДУ. При построении путей к ДУ учитывают потоки информации, проходящие по сети согласно построенным ранее первым и вторым путям к центральному узлу. Для учета существующих на сети потоков информации в эвристическом алгоритме изменяют лишь подсчет экономии при замене одного пути на другой.

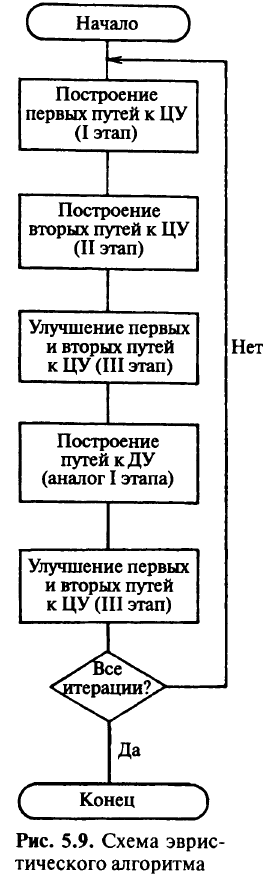
Итерационный процесс продолжают до тех пор, пока осуществление очередной итерации приводит к изменению сети и потоков на ней или пока не будет исчерпан заданный лимит итераций. В качестве решения задачи принимают тот вариант сети, при котором достигается минимальное значение обшей стоимости сети. Как показал опыт многих экспериментальных расчетов, требуемое для достижения миниму- и вторых путей Нет ма число итераций зависит от соотношения величин Pl\ и Чем ближе эти значения, тем больше требуется итераций (но их число, например, не превышало 5 при N= 25). Если же потребности путей к запасному узлу существенно меньше потребностей к центральному узлу, то лучший результат, как правило, достигается на первой итерации.

Построение сети с учетом ограничений по транзитам. Доработку изложенного алгоритма для построения сети и распределения каналов с учетом офаничения по транзитам осуществляют следующим образом.

Под фанзитностью пути понимают число дуг в этом пути. Офаничение на фанзитность формулируют так: построить сеть, в которой число дуг в маршрутах прямых и обходных путей к ЦУ и путей к дополнительному узлу ДУ не

будет превышать некоторого заданного числа (обозначим его т). Для этого достаточно на шаге 2 этапов I—III описанного алгоритма рассмафивать в качестве новых только пути, удовлетворяющие условию фанзитности.

Для вершины необходимо знать:

1) число дуг на участке пути между -й вершиной и вершиной, наиболее удаленной от 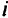-й по числу дуг, путь от которой проходит через прямой или обходной путь от 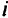-й вершины к ЦУ и путь от 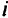-й вершины кДУ. Обозначим эти числа соответственно

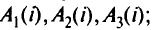
2) число дуг в прямом и обходном путях к ЦУ, а также в пути к ДУ от 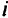-й вершины; обозначим эти числа соответственно

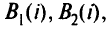
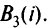
В процессе учета ограничения по транзитам при построении прямых путей к ЦУ и замене пути

в качестве r берем лишь те вершины, для которых выполняется неравенство

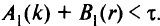
Если от к-й вершины, которая соединена с центром фиктивной дугой, нет маршрута, удовлетворяющего ограничению потран-зитности, то путь от 4-й вершины строят без ограничения на транзитность после того, как построены все маршруты прямых путей, удовлетворяющие ограничению на транзитность.

При построении нового маршрута обходного пути с учетом ограничения по транзитное™ для к-й вершины в качестве вариантов замены рассматриваютлишьтакие вершины г, для которых выполняются требования:

1) если новый маршрут пройдет через прямой путь от r, то

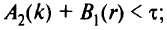
2) если новый маршрут пройдет через обходной путь от r, то

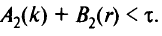
Если вершина k соединена с центром фиктивной дугой и нет маршрута, удовлетворяющего требованию транзитности, то маршрут от к строят без ограничения на транзитность после построения всех маршрутов обходных путей, которые удовлетворяютограничению на транзитность.

Учет ограничения на транзитность на этапе оптимизации построения прямых и обходных путей показан на рис. 5.10. Здесь —

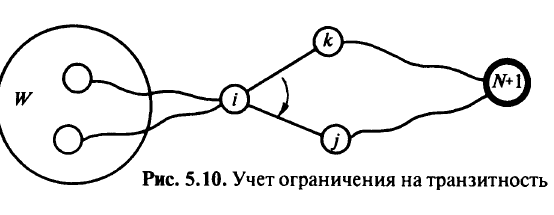
множество вершин, пути от которых проходят по дуге 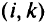. Замена дуги 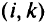на дугу 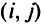на этом этапе происходит при следующих условиях:

1) транзитность пути от 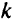-й вершины (старый путь) не меньше транзитности пути от 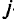-й вершины (новый путь); замену производят, если при этом есть выгода (если экономия положительна);

2) транзитность пути от 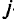-й вершины превышает транзитность пути от вершины к;

3) если ранее построенный путь от 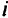-й вершины не удовлетворял ограничению на транзитность, то замена происходит в том случае, когда она выгодна;

4) если путь от 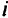-й вершины удовлетворял ограничению на транзитность, но путь хотя бы от одной вершины из множества 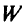(рис. 5.10) многотранзитный, то замену производят тогда и только тогда, когда, во-первых, она выгодна и, во-вторых, если при этом не появляются новые недопустимые по транзитности маршруты (прежние могут оставаться многотранзитными);

5) если путь от вершины 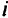и путь от любой другой вершины из множества 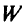удовлетворяют ограничению на транзитность, то замену производят, когда она выгодна и не создает недопустимых по транзитности маршрутов.

При построении путей к ДУ учет ограничения по транзитам проводится следующим образом. При замене

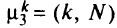
на путь

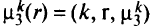
проверяют выполнение неравенства

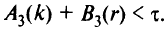
После каждого изменения маршрутов производят пересчет чисел А и В у тех вершин, в маршруты которых были внесены изменения.

Рассмотренный эвристический алгоритм не накладывает серьезных ограничений на функцию стоимости дуг и может быть использован для решения широкого круга задач:

• построения сети кратчайшей длины или минимальной стоимости;

• построения сети минимальной по величине задействованных канало-километров;

• распределения маршрутов на сети при наличии ограничений пропускных способностей дуг с целью достижения максимальной суммарной свободной емкости.

Кроме того, алгоритм позволяет легко учесть дополнительные требования по качеству передачи информации, например ограничение на транзитность. Gримеры синтеза сети с детерминированными исходными данными. Для иллюстрации работы эвристического алгоритма рассмотрим граф, который приведен на рис. 5.11, где изображены допустимые трассы прокладки кабеля с указанием протяженности каждой дуги графа в километрах. Центральным считают узел 1, а дополнительным — узел 2. Потребности в каналах первого и второго путей к ЦУ и пути к ДУ для каждого узла сети приведены в табл. 5.10. Стоимость 1 км дуги зависит от стоимости системы передачи, установленной на дуге, и составляет 2 тыс. руб. при емкости 120 ка-

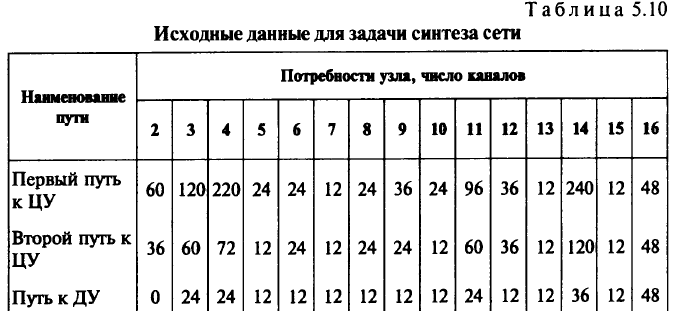
налов, 4 тыс. руб. при емкости 240 каналов и 5 тыс. руб. при емкости 600 каналов. Такой вид функции стоимости линий связи в общем виде соответствует реальной ситуации. Кроме того, в проектируемой сети между узлами I и 2 уже имеется система передачи емкостью 480 каналов, между узлами и 1 и 3 — 600 каналов, между узлами 2 и 8, 3 и 15 — по 120 каналов.

В табл. 5.11 приведены результаты расчетов по описанному алгоритму. Суммарное число свободных каналов на сети вычисляют

как суммарную разность между емкостью установленной системы передачи и потоком информации на каждой дуге. Дуги, включенные в оптимальную сеть, изображены на рис. 5.11 жирными линиями, в скобках указано число используемых каналов на дуге.

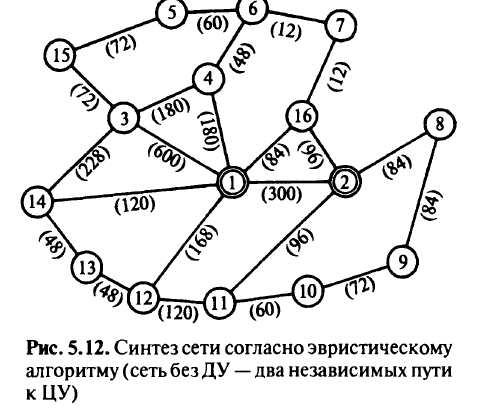
На рис. 5.12 приведена сеть, полученная в результате работы эвристического алгоритма построения двух независимых путей к ЦУ без ДУ. Стоимость этой сети составила 2124 тыс. руб. Маршруты первых и вторых путей сети существенно отличаются от маршрутов первых и вторых путей на рис. 5.11, т.е. при выполнении итерационного процесса эти маршруты претерпевают значительные изменения.

Следует отметить, что требование наличия путей к ДУ увеличивает общую потребность в линиях связи по первому и второму путям к ЦУ на 15,7%, а суммарную стоимость сети — на 7,3%.

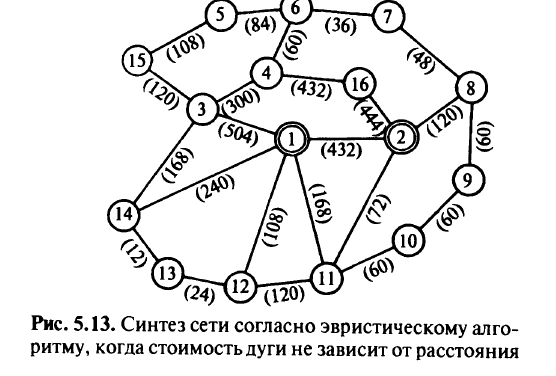
При тех же исходных данных с ЦУ и ДУ был проведен расчет в случае, когда стоимость дуги не зависит от расстояния, а определяется только используемой системой передачи. Стоимость системы передачи емкостью 120 каналов составила 2 тыс. руб.; 240 каналов — 4 тыс. руб.; 600 каналов — 5 тыс. руб. Сеть, полученная в результате работы предложенного алгоритма, приведена на рис. 5.13. Число дуг сети — 23. Протяженность сети — 1132 км. Суммарная свободная емкость — 2460 каналов.

Эта теория взята со страницы лекций по предмету «математическое программирование»:

Предмет математическое программирование

Возможно эти страницы вам будут полезны:

Приближенное решение многопродуктовой транспортной задачи методом агрегирования

Приложения задач о многопродуктовом потоке

Методы внутренней точки для задачи математического программирования

Методы внешней точки для задачи математического программирования