Естественные уравнения движения
Во многих случаях описание движения материальной точки в декартовых неподвижных осях координат вызывает ряд неудобств. Тогда приходится искать другие системы координат, в которых это движение описывается более просто. Одна из таких систем координат может быть определена сопровождающим трехгранником Фре-не, который образуется касательной к траектории точки, главной нормалью и бинормалью. Такие оси называются естественными осями координат. Как известно из кинематики, проекции абсолютного ускорения точки на естественные оси координат имеют вид
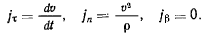
Обозначая проекции силы на соответствующие оси координат через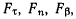 
сразу же получим уравнения движения материальной точки в проекциях на естественные оси координат, или, как их еще называют, естественные уравнения движения
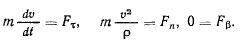
Из этих уравнений видно, что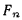 
всегда положительна, a 
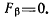Таким образом, сила, действующая на материальную точку, всегда расположена в соприкасающейся плоскости к траектории точки и направлена в сторону вогнутости траектории.
Если сила постоянно направлена по нормали к траектории, то 
откуда следует, что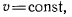 
т. е. точка движется равномерно. Если же сила постоянно направлена по касательной к траектории точки, т. е. 
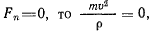и так как 
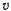не равно тождественно нулю, то траектория точки — прямая линия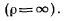 
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Основные законы динамики |
| Две основные задачи динамики |
| Основные теоремы динамики для свободной материальной точки |
| Движение тяжелой материальной точки в пустоте |
