Естественные уравнения движения материальной точки
В случае, когда известна траектория движения точки, бывает удобно проектировать векторное равенство
не на оси декартовых координат, а па естественные оси координат, т.е. на направления касательной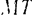 
, главной нормали 
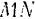и бинормали 
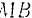(рис. 166).
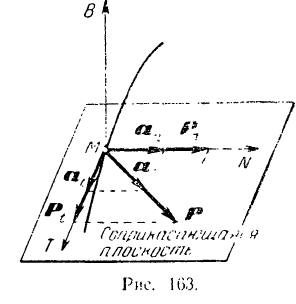
Из кинематики (§ 48) известно, что проекция ускорения на касательную
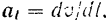
проекция ускорения па главную нормаль
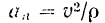
и проекция ускорения на бинормаль
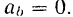
Проектируя векторное равенство
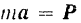
на естественные оси координат и обозначая проекцию силы на касательную через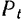 
, проекцию силы на нормаль через 
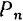и проекцию силы на бинормаль через 
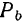, будем иметь:
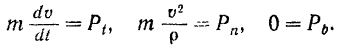
Если на точку действуют несколько сил, то под 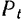, 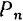и 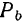в уравнениях (112) надо понимать алгебраические суммы проекций всех сил на соответствующие оси.
Уравнения (112) называются естественными уравнениями движения материальной точки.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
