Оглавление:





Естественная конвекция
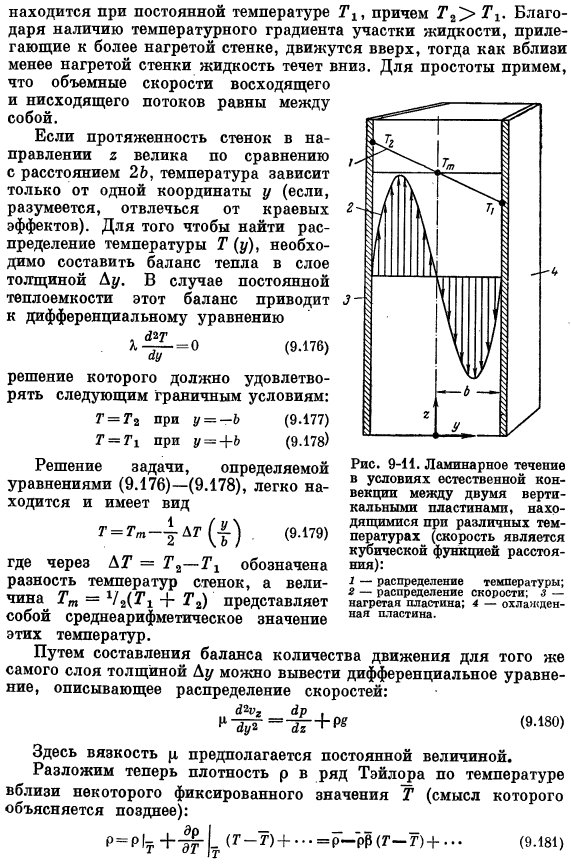
- В разделе 9.8 описана задача теплопередачи в условиях вынужденной конвекции. Целью данного раздела является обсуждение вопросов, связанных с естественной конвекцией. Для наглядности рассмотрена задача течения жидкости между двумя параллельными вертикальными стенками с различными температурами. Расстояние между стенками должно быть 2b (рис. 9-11). Как и раньше, плотность и вязкость жидкости обозначим через p и q соответственно ось y перпендикулярна стене, и на 1 (y =-b) стены всегда поддерживается постоянная температура Т₂, а на 2-й стене(Y = + b). Постоянная температура Tₗₜ и 2 ″ ₃ > t^. Вязкость Р выглядит следующим образом: ожидаемая постоянная.
Теперь мы расширяем плотность p ряда температур Тейлора вокруг некоторого фиксированного значения T(последствия обсуждаются позже) р = п | =(r_f)+… = p_pp (T_f)+… (9.181) В этом расширении p представляет плотность жидкости при температуре T, а p представляет объемный коэффициент Расширение*соответствует температуре T. расширение(9.181) можно считать уравнением состояния»Тейлора».Если вы назначаете первые 2 члена ряда (9.181) формуле (9.180)、 Мы получаем: d2ydydy * 。 ДП ДЗ + ПГ — ^ г(т-т’₎ (9.182) Если градиент давления в системе определяется только весом жидкости, заключенной в стенку, то dpldz = — pg.
Анализ ламинарного переноса тепла при условиях, ожидаемых при аэродинамическом нагреве, затруднен тем фактом, что при больших скоростях полета, которые мы рассматриваем (числа Маха до 10 и больше), по всему пограничному слою проходят очень большие изменения температуры. Людмила Фирмаль
В этом случае уравнение движения принимает вид: — Р₽г (йо) (9-183) Физический смысл этого уравнения заключается в том, что в рассматриваемой системе вязкая сила уравновешивается именно подъемной силой. Подставим формулу для распределения температуры(9.179) в Формулу (9.183).В результате, вы можете увидеть следующее: «+Тег(Т)] «’ 1м> Граничные условия, которым должно удовлетворять распределение скорости:: x = 0 для y—b(9.185) если p = + b, то k0 = 0(9.186) Решение задачи, которое определено в уравнении (9.182)-(9.186), имеет вид: ■>»=(П’-Лц-ч + я) (9.187) Где A = 6 (Tn-7) / DT и μ= y / b.
- Здесь общий объемный поток жидкости в направлении z равен нулю, то есть условия Г » РЛ)= о (9.188). Коэффициент объемного расширения определяется соотношением (9.181 в) Подставляя распределение условия (9.188) (9.187), получаем: — ■Джа + ИА = о Так что это будет A = 0, то есть T = Tm. Таким образом, окончательная формула для распределения скорости имеет вид: (9.190) Анализ показывает, что неоднородное температурное поле, существующее в пространстве между двумя вертикальными стенками, вызывает появление подъемной силы в жидкости, заполняющей это пространство. Наличие подъемной силы приводит к тому, что в жидкости возникает неравномерный профиль скорости.
Профиль, описываемый формулой (9.190), показан на рисунке. 9-11.Такие профили обычно реализуются в колонне Клузиуса-Дикеля, которая предназначена для разделения изотопов или органических жидких смесей. Функции этих колонн основаны на использовании комбинации эффекта термодиффузии и естественной конвекции. Явление термодиффузии подробно рассматривается в главе 17.
Как следствие этого первостепенными задачами в развитии таких самолетов и ракет являются правильный выбор материала и метод охлаждения поверхности. Людмила Фирмаль
В заключение следует отметить, что с учетом безразмерной скорости = Lig / p формула (9.190) может быть описана в несколько ином виде. Из уравнения(9.190) видно, что безразмерная скорость связана с безразмерной длиной следующим соотношением:: Т = — й-или (тр Вот, гр представляет собой так называемое число Грассхофф. Гр.= Вот, Dp = p!- П₂.
Вторая форма записи числа Грассгофа получается из разложения плотности ряда Тейлора выше[эталонное разложение (9.181) 1.In Глава 10, трава в ее наиболее распространенной форме Применение гр при построении экспериментальной корреляции коэффициентов теплопередачи описано в главе 13. Вопрос для обсуждения 1.Сравните 4 системы с различными типами источников тепла. Роль. Гластонов, бринкма Профиль» Результаты d] отношение b определяется коротким? Вы это рекомендуете? Элегантный Раздел пература? 13.Какой лузер, pronzo! (9.74), фут = 7 14.Что будет дальше?] (9.140) при охлаждении Укоротить?
Смотрите также:
| Теплоперенос внутри ребристой поверхности нагрева | Распределения температуры в твердых телах и в ламинарных потоках. Задачи |
| Вынужденная конвекция | Уравнения сохранения энергии |

