Энергетические соотношения в цепях синусоидального тока
В разделе 2.5 рассмотрены энергетические соотношения в отдельных элементах (сопротивлении, индуктивности, емкости) при синусоидальном токе.
Проанализируем энергетические процессы в пассивном двухполюснике (рис. 2.10,6), входное напряжение которого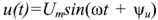 
и входной ток 
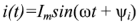изображены на рис.2.16.
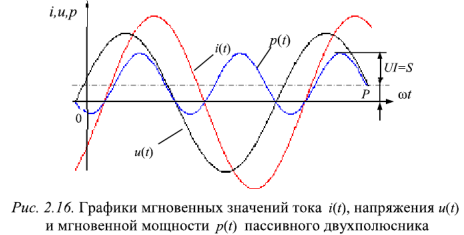
Мгновенное значение мощности синусоидального тока равно произведению мгновенных значений напряжения и тока:
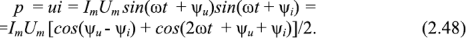
Если учесть, что действующие значения гармонического напряжения и тока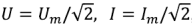 
, а разность начальных фаз напряжения и тока 
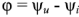, то выражение (2.48) преобразуется к виду:
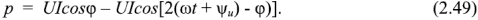
Так как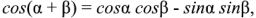 
то
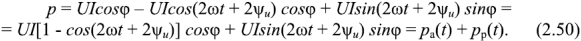
Таким образом, мгновенное значение мощности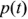
имеет две составляющие 
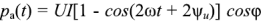и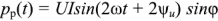 
, периодически изменяющиеся с частотой 
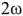. Вследствие этого мгновенное значение мощности 
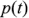также изменяется с двойной частотой (рис. 2.16). Как видно из рис 2.16, 
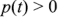, если ток и напряжение совпадают по направлению, 
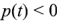, если напряжение и ток имеют разные знаки.
Если мощность положительна, то электрическая энергия передается от источника приемнику, и, наоборот, приемник возвращает энергию источнику при отрицательной мощности.
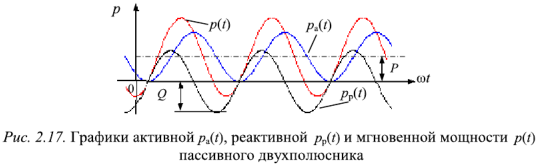
Составляющая мгновенной мощности 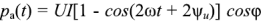cosy колеблется с удвоенной частотой около уровня 
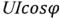и всегда положительна (рис.2.17). Это означает, что электрическая мощность 
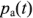, поступающая в пассивный двухполюсник, полностью и необратимо преобразуется в нем в какие-либо виды неэлектрической энергии, например, тепловую или механическую.
В большинстве случаев это полезная мощность, передаваемая от источника электрической энергии приемнику. Поэтому 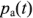называют активной мгновенной мощностью.
Для количественной оценки энергетических процессов в пассивном двухполюснике удобнее использовать не мгновенное значение мощности, а ее среднее за период тока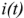 
значение
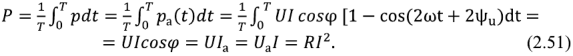
Таким образом, среднее значение мощности равно постоянной составляющей мгновенного значения мощности и равно амплитуде активной мгновенной мощности. Средняя мощность характеризует интенсивность передачи энергии от источника к двухполюснику и се необратимые преобразования в другие виды энергии.
Из выражения (2.51) видно, что активный ток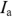 
и активное напряжение 
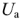соответствуют той части тока или напряжения, которая необратимо расходуется на преобразование энергии в двухполюснике. Активная мощность измеряется в ваттах (Вт).
Мощность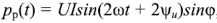 
, представленную вторым слагаемым в выражении (2.50), называют мгновенной реактивной мощностью. Она, как и мгновенная активная мощность, изменяется с удвоенной частотой (рис. 2.17), но ее среднее за период тока 
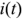значение равно нулю, т.е. в отличие от активной мгновенной мощности мгновенная реактивная мощность не расходуется необратимо на преобразование электрической энергии.
При положительном значении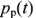 
электрическая энергия поступает из сети в реактивные элементы двухполюсника и накапливается в них. При отрицательном значении 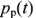ранее накопленная в реактивных элементах двухполюсника энергия возвращается в есть.
Таким образом, в пассивном двухполюснике идет незатухающий колебательный процесс обмена энергией между сетью (источником электрической энергии) и реактивными элементами двухполюсника. Интенсивность этого обмена характеризуется реактивной мощностью, численно равной амплитуде мгновенной реактивной мощности,
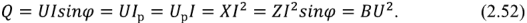
Из этого выражения следует, что реактивный ток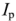 
и реактивное напряжение 
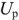соответствуют той части тока или напряжения, которая расходуется на формирование магнитных или электрических полей в реактивных элементах двухполюсника. Реактивная мощность измеряется в вольт-амперах реактивных (Вар).
Величину, равную произведению действующих значений тока и напряжения на зажимах двухполюсника
называют полной или кажущейся мощностью. Амплитуда мгновенной мощности (2.50) численно равна полной мощности. Полная мощность измеряется в вольтамперах (ВЛ).
Из (2.51) и (2.53) следует, что коэффициент мощности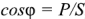 
, т.е. 
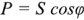. Последнее выражение позволяет определить полную мощность, как максимально возможную активную мощность, т.е. активную мощность при 
.
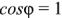Из выражений (251) (2.53) можно получить:
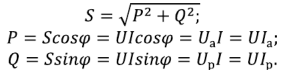
Полная, активная и реактивная мощности соответствуют сторонам прямоугольного треугольника, называемого треугольником мощностей и подобного треугольникам сопротивлений, проводимостей, напряжений и токов.
Комплексной мощностью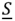 
пассивного двухполюсника называют величину
где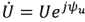 
— комплексное напряжение, 
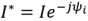— сопряженный комплексный ток. В соответствии с (2.27) комплексное напряжение на входе двухполюсника 
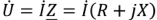. Тогда комплексная мощность
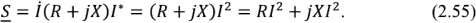
Таким образом, вещественная составляющая комплексной мощности является активной мощностью (2.51), а мнимая составляющая — реактивной мощностью (2.52) пассивного двухполюсника.
Множитель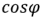 
в выражении (2.51) носит название коэффициента мощности. Как видно из этого выражения, активная мощность равна произведению действующих значений напряжения и тока, умноженному на коэффициент мощности. Чем ближе угол 
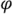к нулю, тем ближе 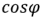к единице и, следовательно, тем меньше требуется величина тока 
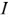, при которой заданная средняя мощность 
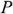при данном напряжении 
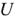будет передана от источника энергии двухполюснику (приемнику).
Высокий коэффициент мощности нужен также и для снижения потерь в линии передачи электрической энергии от се источника потребителю. Действительно, ток в линии определяется нагрузкой и равен, как следует из (2.51)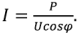 
Отсюда потери энергии в линии с сопротивлением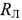 
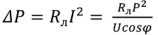
возрастают с уменьшением коэффициента мощности.
Именно поэтому повышение коэффициента мощности промышленных электроустановок представляет важную технико-экономическую задачу.
Баланс мощности является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи.
Как указывалось в разделе 1.4,5 в любой цени постоянного тока соблюдается баланс мощности: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи. Математическая форма записи баланса мощности для электрической цепи, содержащей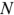 
источников напряжения и 
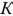пассивных элементов, имеет вид:
Баланс мощности в электрической цепи синусоидального тока, содержащей 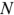источников энергии,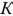 
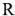-элементов, 
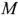индуктивных элементов и 
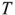емкостных элементов, означает:
алгебраическая сумма активных мощностей всех источников энергии равна арифметической сумме мощностей всех резистивных элементов:
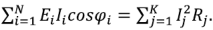
или
алгебраическая сумма реактивных мощностей всех источников энергии равна алгебраической сумме мощностей всех индуктивных и всех емкостных элементов:
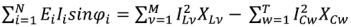
или
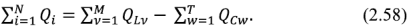
Согласование источника синусоидального сигнала с нагрузкой.
Согласованным режимом работы электрической цепи принято считать режим передачи наибольшей мощности от источника к нагрузке.
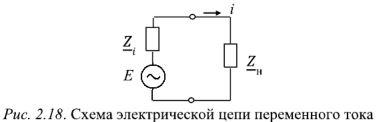
Схема включения источника синусоидального сигнала и нагрузки показана на рис. 2.18. В этой схеме источник синусоидального сигнала представлен источником напряжения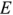 
с внутренним комплексным сопротивлением 
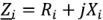, а нагрузка — комплексным сопротивлением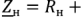 
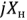
Активная мощность, выделяемая в нагрузке,
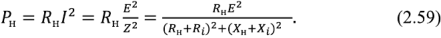
Из приведенной формулы видно, что выделяемая в нагрузке мощность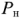 
будет максимальной, если 
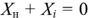, т.е. если реактивные сопротивления источника и нагрузки одинаковы по модулю, но противоположны по знаку. Это означает, что при индуктивном реактивном сопротивлении нагрузки реактивное сопротивление источника должно быть емкостным и наоборот. В этом случае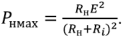 
От источника к нагрузке будет передаваться наибольшая мощность, если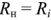 
. Величина наибольшей мощности
Таким образом, согласование источника синусоидального сигнала с нагрузкой сводится к подбору сопротивлени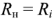й 
и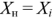 
.
Коэффициент полезного действия для схемы, представленной на рис. 2.18, равен отношению активной мощности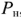 
выделяемой в нагрузке, к активной мощности 
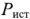, генерируемой источником сигнала. В согласованном режиме
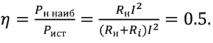
Эта теория взята со страницы помощи с заданиями по электротехнике:
Возможно эти страницы вам будут полезны:
| Пассивный двухполюсник |
| Сопротивление, индуктивность и емкость в цепи синусоидального тока |
| Последовательное соединение R-, L-, C- -элементов |
| Параллельное соединение R-, L-, C-элементов |
