Эллиптический параболоид
Исследуем поверхность, заданную уравнением

(12.33) где 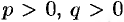 . Рассечем поверхность (12.33) плоскостями
. Рассечем поверхность (12.33) плоскостями 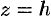 . В сечении получим линию, уравнения которой есть
. В сечении получим линию, уравнения которой есть
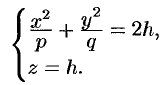
Если 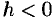 , то плоскости
, то плоскости 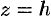 поверхности не пересекают; если
поверхности не пересекают; если 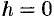 , то плоскость
, то плоскость 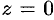 касается поверхности в точке (0; 0; 0); если
касается поверхности в точке (0; 0; 0); если 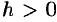 , то в сечении имеем эллипс, уравнение которого имеет вид
, то в сечении имеем эллипс, уравнение которого имеет вид
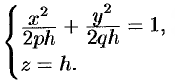
Его полуоси возрастают с ростом 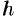 .
.
При пересечении поверхности (12.33) координатными плоскостями
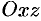 и
и 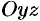 получатся соответственно параболы
получатся соответственно параболы 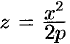 и
и 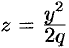 . Таким образом, поверхность, определяемая уравнением (12.33), имеет вид выпуклой, бесконечно расширяющейся чаши (см. рис. 94). Поверхность (12.33) называется эллиптическим параболоидом.
. Таким образом, поверхность, определяемая уравнением (12.33), имеет вид выпуклой, бесконечно расширяющейся чаши (см. рис. 94). Поверхность (12.33) называется эллиптическим параболоидом.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Однополостный гиперболоид |
| Двухполостный гиперболоид |
| Гиперболический параболоид |
| Конус второго порядка |

