Эллипсоид
Исследуем поверхность, заданную уравнением

Рассмотрим сечения поверхности (12.28) с плоскостями, параллельными плоскости 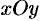 . Уравнения таких плоскостей:
. Уравнения таких плоскостей: 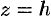 , где
, где 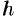 — любое число.
— любое число.
Линия, получаемая в сечении, определяется двумя уравнениями
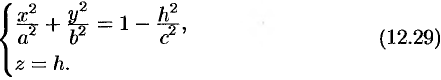
Исследуем уравнения (12.29):
а) Если 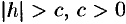 , то
, то 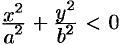 . Точек пересечения поверхности (12.28) с плоскостями
. Точек пересечения поверхности (12.28) с плоскостями 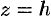 не существует.
не существует.
б) Если 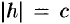 , т. е.
, т. е. 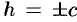 , то
, то 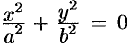 . Линия пересечения (12.29) вырождается в две точки
. Линия пересечения (12.29) вырождается в две точки 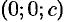 и
и 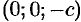 . Плоскости
. Плоскости 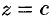 и
и 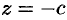 касаются данной поверхности.
касаются данной поверхности.
в) Если 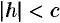 , то уравнения (12.29) можно переписать в виде:
, то уравнения (12.29) можно переписать в виде:
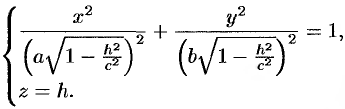
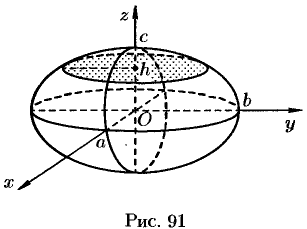
Как видно, линия пересечения есть эллипс с полуосями (см. рис. 91)
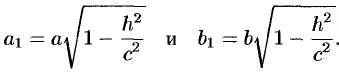
При этом чем меньше 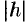 , тем больше полуоси
, тем больше полуоси 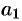 и
и 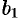 . При
. При 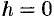 они достигают своих наибольших значений:
они достигают своих наибольших значений: 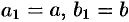 . Уравнения (12.29) примут вид
. Уравнения (12.29) примут вид
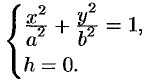
Аналогичные результаты получим, если рассмотрим сечения поверхности (12.28) плоскостями 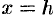 и
и 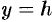 .
.
Таким образом, рассмотренные сечения позволяют изобразить поверхность (12.28) как замкнутую овальную поверхность. Поверхность (12.28) называется эллипсоидом. Величины 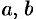 и
и 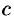 называются полуосями эллипсоида. Если все они различны, то эллипсоид называется трехосным, если какие-либо две полуоси равны, трехосный эллипсоид превращается в эллипсоид вращения-, если
называются полуосями эллипсоида. Если все они различны, то эллипсоид называется трехосным, если какие-либо две полуоси равны, трехосный эллипсоид превращается в эллипсоид вращения-, если 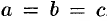 , то — в сферу
, то — в сферу 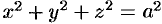 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Уравнение плоскости в отрезках |
| Нормальное уравнение плоскости |
| Однополостный гиперболоид |
| Двухполостный гиперболоид |

