Эллипсом называется множество точек на плоскости, сумма расстояний от каждой из которых до двух заданных точек (называемых фокусами) есть величина постоянная (большая, чем расстояние между фокусами). Обозначим эту постоянную величину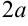 
. Тогда если точки 
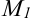и 
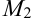принадлежат эллипсу, a 
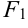и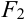 
— фокусы эллипса, то по определению справедливо равенство:
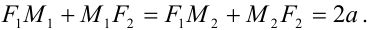
Каноническое уравнение эллипса имеет вид: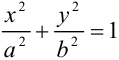 
.
Для построения эллипса нужно из канонического уравнения выделить два параметра: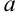 
, 
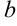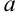( — большая полуось, 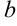— малая полуось)
На оси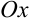 
отметим точк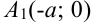и 
и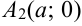 
, на оси 
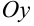— точк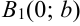и 
и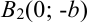 
. Тогда эллипс будет проходить через точки 
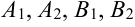следующим образом (рис. 7.2):
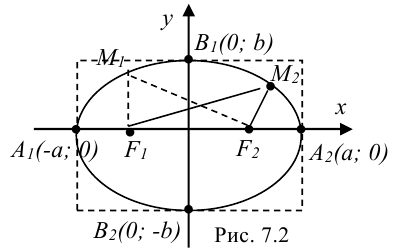
Точки 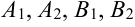называются вершинами эллипса.
Пример №7.3.
Постройте эллипс, заданный уравнением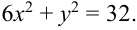 
Решение:
Приведем уравнение эллипса к каноническому виду ( 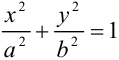), для этого разделим все его члены на 32, чтобы в правой части была 1:
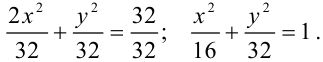
При сравнении с каноническим видом отмечаем, что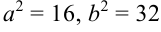 
, откуда 
.
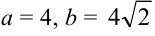Эллипс будет иметь вид (рис. 7.3):
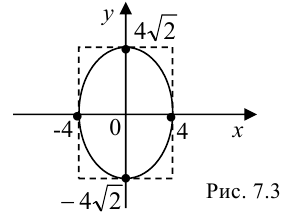
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие кривой второго порядка. |
| Окружность и ее уравнение. |
| Гипербола и ее уравнение. |
| Парабола и ее уравнение. |
