Элементы теории множеств. Базовые понятия и определения
множества, операции над ними
Понятие множества является одним из основных в математике. Оно принадлежит к числу первичных, не определяемых через более простые.
Под множеством будем понимать совокупность объектов, объединенных по какому-либо признаку. Слова «совокупность», «набор», «система», «объединение» и другие являются синонимами слова «множество». Например, можно говорить о множестве студентов в институте, множестве букв в алфавите, множестве целых чисел и т. д. Из приведенных примеров следует, что множество может содержать как конечное, так и бесконечное число объектов некоторой природы. Объекты, из которых состоит множество, называются его элементами или точками. Принадлежность элемента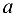 
множеству А обозначают следующим образом: 
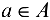. Если 
не является элементом множества А, то пишут: 
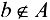. Если 
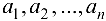— некоторые элементы, то запись 
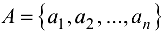означает, что множество А состоит из элементов .
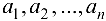Два множества А и В называют равными, если они состоят из одних и тех же элементов (обозначение: А = В ). Множество А называется подмножеством множества В, если все элементы множества А являются одновременно и элементами множества В (обозначение: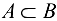 
(«множество А содержится в множестве В») или 
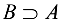(«множество В содержит множество А»). Например, так как всякое натуральное число п является целым, то 
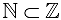, где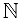 
— множество натуральных чисел, 
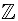— множество целых чисел.
Множество, не содержащее ни одного элемента, будет называться пустым множеством и обозначаться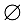 
. Это множество является подмножеством любого множества. Пусть X — множество, а 
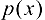— какое-либо свойство элементов этого множества. Тогда запись 
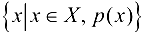означает совокупность тех элементов множества X, которые обладают свойством 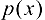. Например, если 
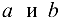— два числа и 
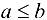, то встречавшиеся в элементарной математике отрезок, интервал и полуинтервалы можно записать в следующем виде: 
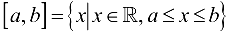— отрезок; 
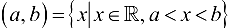— интервал; 
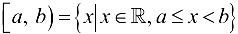и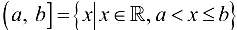 
— полуинтервалы. Здесь 
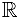— множество действительных (вещественных) чисел.
Множество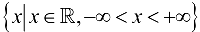 
всех чисел называется также числовой прямой или числовой осью, а любое число — точкой этой прямой.
Пересечением множеств А и В называется множество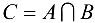 
, состоящее из всех элементов, одновременно принадлежащих как А, так и В, т. е. 
.
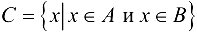Объединением множеств А и В называется множество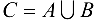 
, состоящее из всех элементов, принадлежащих хотя бы одному из двух данных множеств, т. е. 
.
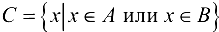Разностью множеств А и В называется множество А/В, состоящее из тех элементов множества А, которые не принадлежат множеству В, т. е.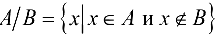 
.
Пусть X — некоторое основное множество, тогда дополнением множества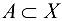 
называется множество 
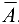, состоящее из всех элементов 
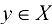и не принадлежащих А, т. е.
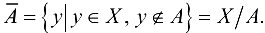
Таким образом, все элементы, которые не принадлежат множеству А, образуют множество 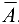. Следовательно, 
.
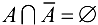Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
| Случай квадратичной зависимости в математическом анализе |
| Случаи сведения функций к линейной зависимости с примерами решения |
| Логические символы в теории множеств |
| Грани числовых множеств |
