Оглавление:
Современная математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования, то есть планирование эксперимента в ходе исследования, то есть последовательный анализ и решает многие другие задачи.
Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.
Если требуется изучить совокупность большого числа однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты, то в таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению. Например, если имеется партия деталей, то качественным признаком может служить стандартность деталей, а количественным — размер деталей.
Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.
Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
Объемом совокупности называют число объектов этой совокупности.
Например, из 100 деталей отобрано 10 деталей, то объем генеральной совокупности 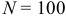 , а объем выборки
, а объем выборки 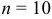 .
.
Повторной называют выборку, при которой отобранный объект перед отбором следующего возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
Выборка должна правильно представлять пропорции генеральной совокупности. Это требование коротко формулируют так: выборка должна быть репрезентативной, то есть представительной.
Если объем генеральной совокупности достаточно велик, а выборка составляет лишь незначительную часть этой совокупности, то различие между повторной и бесповторной выборками стирается.
На практике применяют различные способы отбора, принципиально которые можно разделить на два вида:
- Отбор, не требующий расчленения генеральной совокупности на части. Это простой случайный бесповторный отбор и простой случайный повторный отбор.
- Отбор, при котором генеральная совокупность разбивается на части. Это типичный отбор, механический отбор и серийный отбор.
Простым случайным называют такой отбор, при котором объекты извлекают по одному из всей генеральной совокупности.
Типичным называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой её ’’типической” части.
Типическим отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных типических частях генеральной совокупности.
Например, детали от разных станков.
Механическим называют отбор, при котором генеральную совокупность ’’механически” делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект.
Например, если требуется отобрать 25% изготовленных деталей, то отбирают каждую 4-ую деталь.
Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а ’’сериями”, которые подвергаются сплошному обследованию.
Серийным отбором пользуются тогда, когда обследуемый признак колеблется в различных сериях незначительно. На практике часто используется комбинированный отбор, при котором сочетаются указанные выше способы.
Пусть из генеральной совокупности извлечена выборка, причем x( наблюдалось 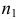 раз,
раз, 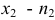 раз,
раз, 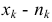 и
и 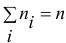 — объем выборки. Наблюдаемые значения
— объем выборки. Наблюдаемые значения 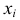 называют вариантами, а последовательность вариант, записанных в возрастающем порядке, — вариационным рядом.
называют вариантами, а последовательность вариант, записанных в возрастающем порядке, — вариационным рядом.
Число наблюдений называют частотами, а их отношения к объему выборки 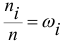 — относительными частотами.
— относительными частотами.
Статическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.
В теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике — соответствия между наблюдаемыми вариантами и их частотами или относительными частотами.
Эмпирической функцией распределения (функцией распределения выборки) называют функцию 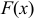 , определяющую для каждого значения
, определяющую для каждого значения 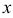 относительную частоту события
относительную частоту события 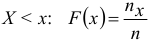 ; где
; где 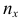 — число вариант, меньших
— число вариант, меньших 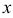 ;
; 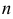 — объем выборки.
— объем выборки.
Функцию распределения генеральной совокупности называют теоретической функцией распределения.
Различие между эмпирической и теоретическими функциями состоит в том, что теоретическая функция 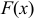 определяет вероятность
определяет вероятность 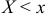 , а эмпирическая функция
, а эмпирическая функция 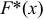 определяет относительную частоту этого же события.
определяет относительную частоту этого же события.
Пример №1
Построить эмпирическую функцию по данным распределения выборки:
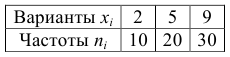
Решение:
Объем выборки 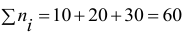 . При
. При 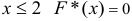 ; при
; при 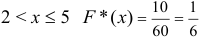 ; при
; при 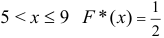 ; при
; при 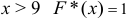 .
.
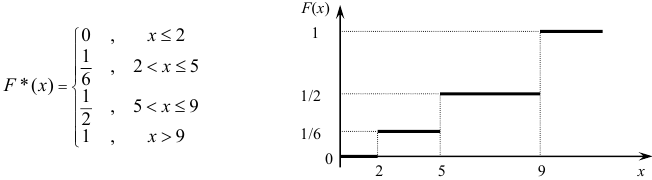
Для наглядности строят различные графики.
Полигоном частот называют ломаную, отрезки которой соединяют точки 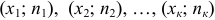 .
.
Полигоном относительных частот называют ломанную, отрезки которой соединяют точки 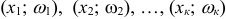 .
.
В случае непрерывного признака целесообразно строить гистограмму.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною 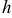 , а высоты равны отношению
, а высоты равны отношению 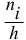 (плотность частот). Площадь
(плотность частот). Площадь 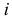 — го частичного прямоугольника равна
— го частичного прямоугольника равна 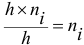 — сумме частот вариант
— сумме частот вариант 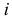 -го интервала, а площадь гистограммы частот равна объему выборки.
-го интервала, а площадь гистограммы частот равна объему выборки.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною 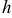 , а высоты равны отношению
, а высоты равны отношению 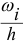 .
.
Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.
Для того чтобы статистические оценки давали “хорошие” приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Если математическое ожидание статистических оценок равно оцениваемому параметру при любом объеме выборки, то есть 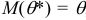 , то статистическую оценку
, то статистическую оценку 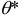 называют несмещенной.
называют несмещенной.
Смещенной называют оценку, математическое ожидание которой неравно ожидаемому параметру.
Статистическая оценка должна быть эффективной.
Эффективной называют статистическую оценку, которая при заданном объеме выборки имеет наименьшую возможную дисперсию.
При рассмотрении выборок большого объема к статистическим оценкам предъявляют требование состоятельности.
Состоятельной оценкой называют статистическую оценку, которая при 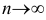 стремится по вероятности к оцениваемому параметру.
стремится по вероятности к оцениваемому параметру.
Если изучается дискретная генеральная совокупность относительно количественного признака 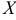 , то генеральной средней
, то генеральной средней 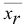 называют среднее арифметическое значений признака генеральной совокупности.
называют среднее арифметическое значений признака генеральной совокупности.
Если все значения признака генеральной совокупности объема 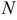 различны, то
различны, то 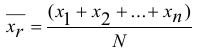 .
.
Если значения признака 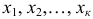 имеют соответственно частоты
имеют соответственно частоты 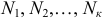 , причем
, причем 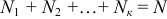 ,
, 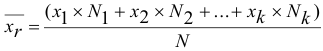 .
.
Выборочной средней 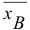 называют среднее арифметическое значение признака выборочной совокупности. Если
называют среднее арифметическое значение признака выборочной совокупности. Если 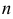 — объем выборки, то
— объем выборки, то 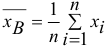 — если значения
— если значения 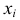 — различны.
— различны.
Если значение признака 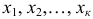 имеют соответственно частоты
имеют соответственно частоты 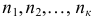 , то
, то
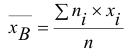
Если по нескольким выборкам достаточно большого объема из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой. В этом состоит свойство устойчивости выборочных средних.
Если все значения количественного признака 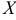 совокупности разбиты на несколько групп, то групповой средней называют среднее арифметическое значений признака, принадлежащих группе.
совокупности разбиты на несколько групп, то групповой средней называют среднее арифметическое значений признака, принадлежащих группе.
Общей средней 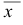 называют среднее арифметическое значений признака, принадлежащих всей совокупности.
называют среднее арифметическое значений признака, принадлежащих всей совокупности.
Общая средняя равна средней арифметической групповых средних, взвешенной по объемам групп.
Пример №2
Найти общую среднюю совокупности, состоящую из двух групп:

Решение:
Найдем групповое среднее
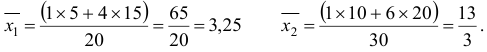
1 способ. Найдем общую среднюю по групповым средним:
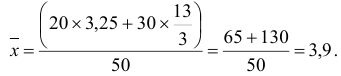
2 способ. Найдем общую среднюю по групповым признакам:
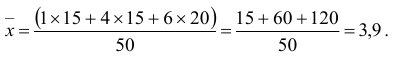
Рассмотрим отклонение между значением признака и общей средней: 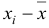 .
.
Теорема. Сумма произведений отклонений на соответствующие частоты равна нулю: 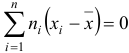 , где
, где 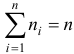 — объем выборки из генеральной совокупности.
— объем выборки из генеральной совокупности.
Следствие. Среднее значение отклонения равно нулю
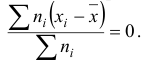
Пример №3
Дано распределение количественного признака 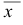
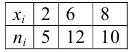
Найти среднее значение отклонения
Решение:
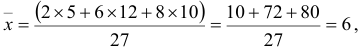
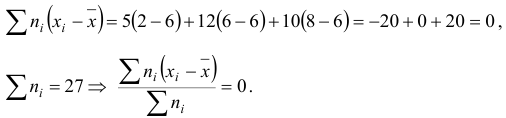
Для того чтобы охарактеризовать рассеяние значений количественного признака 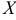 генеральной совокупности вокруг своего среднего значения, вводят генеральную дисперсию.
генеральной совокупности вокруг своего среднего значения, вводят генеральную дисперсию.
Генеральной дисперсией 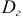 называют средне арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения
называют средне арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения 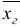 . Если объем равен
. Если объем равен 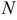 , то
, то
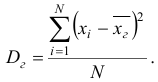
Значения 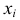 различны и если значения признака
различны и если значения признака 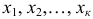 имеют соответственно частоты
имеют соответственно частоты 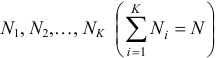 , то
, то
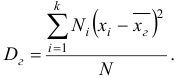
Генеральным средним квадратическим отклонением (стандартом) называют
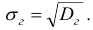
Выборочной дисперсией 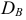 называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения
называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения 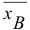 .
.
Если значения 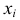 различны, то
различны, то 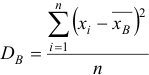 , где
, где 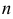 — объем выборки.
— объем выборки.
Если значения признака 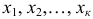 имеют соответственно частоты
имеют соответственно частоты 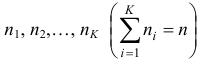 , то
, то 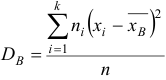 .
.
Теорема (вычисление дисперсии выборочной или генеральной). Дисперсия равна среднему квадратов значений признака минус квадрат общей средней: 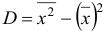 .
.
Пример №4
Найти дисперсию по данному распределению
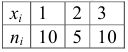
Решение:
Найдем общую среднюю:
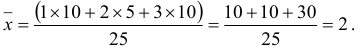
Найдем среднюю квадратов:
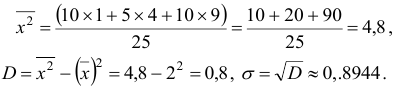
Точечной называют оценку, которая определяется одним числом. При выборе малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Интервальной называют оценку, которая определяется двумя числами-концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.
Пусть найденная по данным выборки статическая характеристика 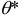 служит оценкой неизвестного параметра
служит оценкой неизвестного параметра 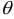 .
.
Надежность (доверительной вероятностью) оценки 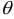 по
по 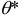 называют вероятность
называют вероятность 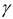 с которой осуществляется неравенство
с которой осуществляется неравенство 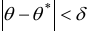 .
.
Обычно надежность оценки задается наперед, причем в качестве 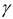 берут число, близкое к единице. Это 0.95, 0.99, 0.999.
берут число, близкое к единице. Это 0.95, 0.99, 0.999.
Доверительным называют интервал 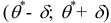 который покрывает неизвестный параметр с заданной надежностью
который покрывает неизвестный параметр с заданной надежностью 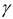 .
.
Доверительный интервал, покрывающий параметр 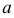 , с надежностью
, с надежностью 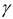 нормального распределения при известном
нормального распределения при известном 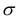 можно определить из уравнения:
можно определить из уравнения: 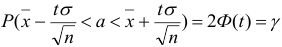 , где
, где 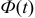 — функция Лапласа,
— функция Лапласа, 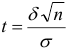 .
.
Следовательно, с надежностью 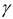 можно утверждать, что доверительный интервал
можно утверждать, что доверительный интервал 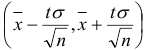 покрывает неизвестный параметр
покрывает неизвестный параметр 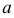 ; точность оценки
; точность оценки 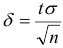 .
.
Пример №5
Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью 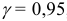 , зная выборочную среднюю
, зная выборочную среднюю 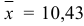 (статистическую среднюю
(статистическую среднюю 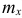 ), объем выборки (число наблюдений)
), объем выборки (число наблюдений) 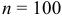 и среднее квадратическое отклонение
и среднее квадратическое отклонение 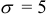 .
.
Решение:
Воспользуемся формулой 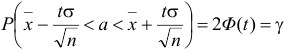 . Найдем
. Найдем 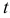 . Из соотношения
. Из соотношения 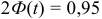 получим
получим 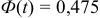 . По таблице приложения находим
. По таблице приложения находим 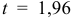 . Подставляя данные в доверительный интервал
. Подставляя данные в доверительный интервал 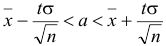 , получаем
, получаем 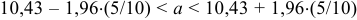 , или окончательно
, или окончательно 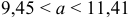 .
.
Приложение 1
Таблица значений функции 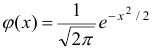
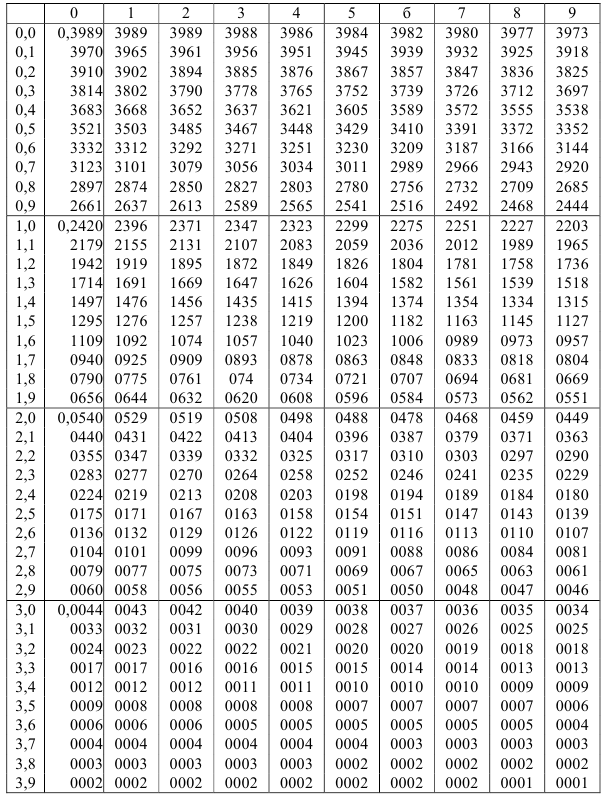
Приложение 2
Таблица значений функции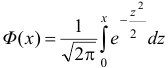

На этой странице размещён краткий курс лекций по теории вероятностей и математической статистике с теорией, формулами и примерами решения задач:
Теория вероятностей краткий курс для школьников и студентов
Возможно вам будут полезны эти страницы:

