Оглавление:
Элементарные преобразования матриц
Элементарными преобразованиями матриц являются:
- перестановка местами двух параллельных рядов матрицы;
- умножение всех элементов ряда матрицы на число, отличное от нуля;
- прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
Две матрицы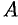 
и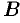 
называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается 
.
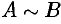При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например
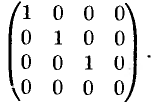
Пример №1.4.
Привести к каноническому виду матрицу
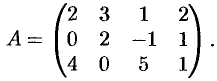
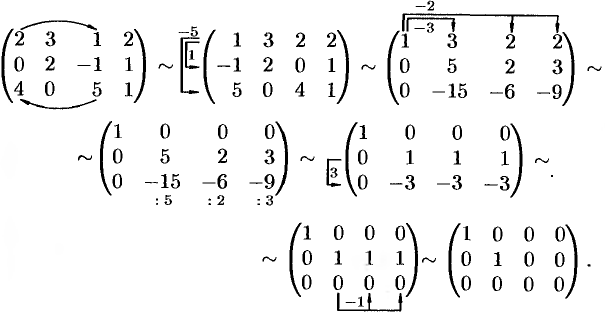
Решение:
Выполняя элементарные преобразования, получаем
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Обратное преобразование Лапласа |
| Действия над матрицами |
| Системы линейных однородных уравнений |
| Линейные операции над векторами |
