Элементарная работа силы
Важное значение в различных вопросах механики имеет скалярная величина, называемая работой силы. Она характеризует эффект действия силы на перемещении ее точки приложения, вызванном этой силой.
Работа силы на бесконечно малом перемещении ее точки приложения называется элементарной работой.
Элементарная работа силы равна скалярному произведению вектора силы на вектор элементарного перемещения точки приложения силы. Обозначая элементарную работ символом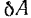 
, будем иметь
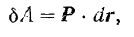
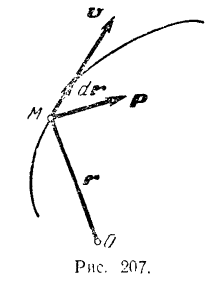
где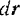 
— вектор элементарного перемещения точки приложения силы или, что все равно (рис. 207), дифференциал радиуса-вектора точки приложения силы.
На основании определения скалярного произведения двух векторов можно записать
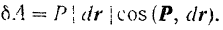
Так как
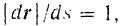
то
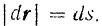
Здесь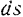 
— длина элементарного перемещения точки приложения (а не дифференциал расстояния) и, следовательно величина положительная. Так как вектор элементарного перемещения точки приложения силы всегда совпадает с направлением скорости этой точки, то
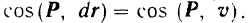
Поэтому равенство для элементарной работы можно переписать в следующем виде:
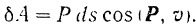
Элементарная работа силы равна произведению модуля силы, длины элементарного перемещения ее точки приложения и косинуса угла между направлениями силы и перемещения (скорости) точки приложения силы.
Если угол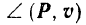 
между направлениями силы и перемещения ее точки приложения будет острым, то в соответствии с формулой (187) работа сил будет положительна. В частности, при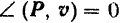 
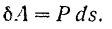
Если угол 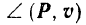будет тупой, то работа силы будет отрицательной. В частности, при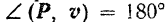 
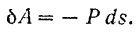
Если же
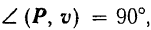
то
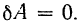
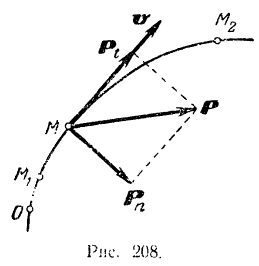
Работа силы на перемещении ее точки приложения, перпендикулярном к направлению силы, равна нулю.
В общем случае, когда направление силы не совпадает с направлением перемещения ее точки приложения (рис. 208), силу можно разложить на две составляющие: касательную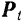 
, направленную по касательной к траектории, и нормальную 
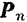, направленную по главной (внутренней) нормали к траектории.
Из формулы (187) видно, что работу на перемещении совершает только касательная составляющая силы, алгебраическое значение которой
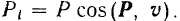
Нормальная же составляющая 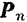не влияет на величину работы силы. Она, как говорят, «не производит работы». Эта составляющая, сообщая точке нормальное ускорение, может лишь изменять направление ее движения (если этому не препятствуют наложенные на точку связи) или изменять давление на связь. В ряде случаев бывает удобно пользоваться иным, чем (186) или (187), аналитическим выражением для элементарной работы силы. Так как
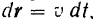
то формула (186) даст
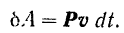
Вспоминая формулу разложения вектора по осям координат, последнее равенстве можно записать в виде:
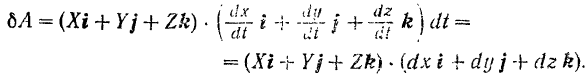
Перемножая многочлены, стоящие в правой части последнего равенства, получаем:
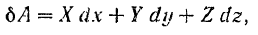
где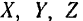 
— проекции данной силы на координатные оси, 
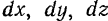— элементарные приращения координат точки приложения силы.
Элементарная работа силы равна сумме произведений проекций силы на оси координат на элементарные приращения соответствующих координат точки приложения силы.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Физический маятник с примерами решения |
| Дифференциальные уравнения плоского движения твердого тела |
| Работа силы на конечном пути с примером решения |
| Графический способ вычисления работы |
