Пример задачи 10.7
Электродвигатель весом Q = 1,5 кН установлен на консольных деревянных балках прямоугольного поперечного сечения при соотношении сторон h / b= 1,5 (рис. 10.12, а).
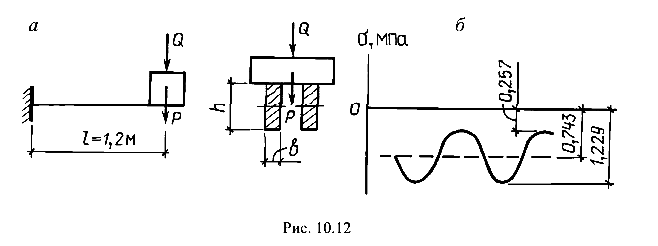
Электродвигатель делает п = 1400 об/мин. Вертикальная амплитуда возмущающей силы Р = 0,4 кН.
Определить размеры поперечного сечения балок, чтобы частота собственных колебаний балок была на 30 % больше частоты возмущающей силы. Для древесины R = 10 МПа, Е=12 ГПа.
Собственным весом балок пренебречь.
Решение
Консольные балки воспринимают вес двигателя Q как статическую нагрузку и дополнительную Р — как динамическую, вызванную работой двигателя.
Обе нагрузки вызывают плоский изгиб балок.
Частота вынужденных колебаний балок
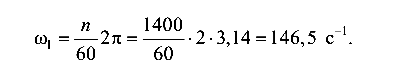
Согласно условию задачи частота собственных колебаний балок 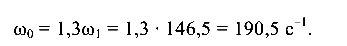
Используя формулу (10.8), запишем
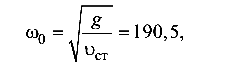
откуда статический прогиб балок
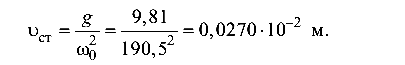
С другой стороны, статический прогиб двух консольно закрепленных балок
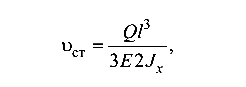
откуда момент инерции сечения одной балки
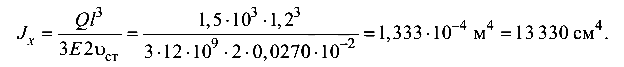
Поскольку момент инерции для прямоугольного сечения 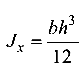 с учетом h / b = 1,5 получим
с учетом h / b = 1,5 получим
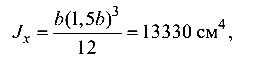
откуда b = 14,75 см, h = 22,1 см.
Конструктивно принимаем h = 22 см,b = 15 см. Момент инерции принятого сечения 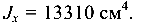
Для принятых размеров сечения балки частота собственных колебаний

что соответствует требованию расчета.
Вычислим динамические напряжения в балке. Для сечений балок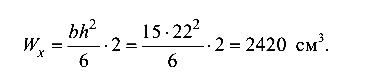
Нормальное напряжение в балках от статического действия силы Q
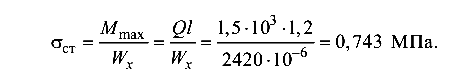
Значение динамического коэффициента по формуле (10.9)
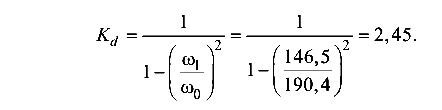
Напряжения от возмущающей силы
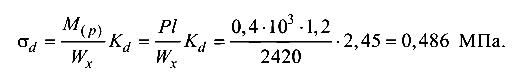
Напряжение в крайних точках опасного сечения балок (в защемлении) будет меняться (по формуле (10.10)) в следующих пределах (рис. 10.12,б):
Максимальное напряжение составляет небольшую часть расчетного сопротивления. Это вызвано необходимостью обеспечения работы конструкции вне зоны резонанса.
Вычислим динамический прогиб балок.
Статический прогиб от веса Q
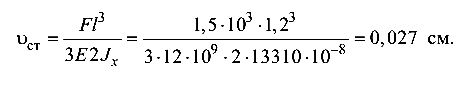
Амплитуда вынужденных колебаний от возмущающей силы Р
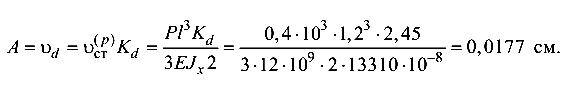
Максимальный прогиб конца балки (по выражению (10.11))
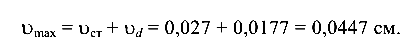
Максимальный относительный прогиб
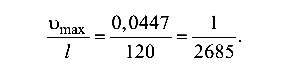
Этот пример решения задачи взят со страницы решения задач с примерами по всем темам предмета «Сопротивление материалов»:
Примеры решения задач по сопротивлению материалов
Дополнительные задачи которые вам будут полезны:
