Оглавление:
Основные понятия
Периодическими несинусоидальными токами называют токи, изменяющиеся в времени по периодическому несинусоидальному закону.
Несинусоидальные токи возникают при различных режимах работы электрических цепей. Таких режимов четыре.
- Источник электрической энергии вырабатывает несинусоидальную ЭДС или несинусоидальный ток, а все элементы цепи (активные сопротивления, индуктивности и ёмкости) линейны, т.е. от величины тока не зависят.
- Источник электрической энергии вырабатывает синусоидальную ЭДС, но один или несколько элементов цепи нелинейны, т.е. имеют нелинейные характеристики (катушки со стальным сердечником, выпрямители).
- Источник электрической энергии вырабатывает несинусоидальную ЭДС, ЭДС, а в электрическую цепь входит одно или несколько нелинейных сопротивлений.
- Источник электрической энергии вырабатывает постоянную или синусоидальную ЭДС, а один или несколько элементов цепив процессе работы изменяют свои параметры.
Гармоники
При рассмотрении периодических несинусоидальных колебаний можно воспользоваться теоремой Фурье, согласно которой любая периодически изменяющаяся величина может быть представлена в виде суммы постоянной составляющей и ряда синусоидальных составляющих с кратными частотами.
Синусоидальные составляющие несинусоидальных колебавний называются гармониками.
Синусоидальная составляющая, частота которой равна частоте несинусоидальной периодической величины, называется основой, или первичной, гармоникой. А синусоидальные составляющие, частоты которых в 2,3, …,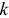
раз больше частоты несинусоидальной величины, называются соответственно 2-й, 3-й, 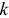-ой гармоникой.
Аналитическое выражение несинусоидальной функции можно записать так:
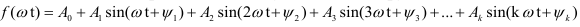
где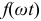 
— несинусоидальная величина, изменяющаяся с частотой 
. 
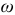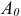— постоянная составляющаяся несинусоидальной величины; 
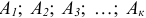— амплитуды соответственно 1-й, 2-й, 3-й, 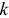-й, гармоник, т.е. синусоидальных составляющих с частотой 
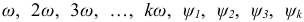— начальные фазы соответственно 1-й, 2-й, 3-й и 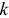-й гармоник.
Гармоники можно преобразовать, применив из тригонометрии формулу синуса суммы углов. 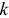-ю гармонику можно представить в виде
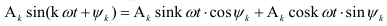
Обозначив постоянные величины выражения можно получить
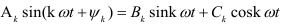
Тогда ряд Фурье для несинусоидальных периодической функции, примет вид
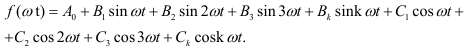
В отличии от амплитуды 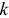-й гармоники 
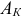, постоянные величины 
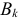и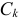 
могут быть положительными или отрицательными. Такая запись характерна тем, что гармоники составляются ряд синусов и ряд косинусов с начальными фазами, равными нулю 
.
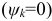Свойства периодических кривых Несинусоидальные переодические кривые, с которыми приходится встречаться в электротехнике, являются симметричными относительно оси абсцисс или ординат или начала координат.
Периодическая кривая называется симметрической относительно абсцисс, если на расстоянии половины периода они имеют ординаты, одинаковые по величине, но обратные по знаку (рис. 12.1 а), т.е. отрицательная полуволна такой кривой представляет собой зеркальное изображение положительной полуволны. Кривые симметрые относительно оси абсцисс, не содержат постоянной составляющей и четных гармоник. Такая кривая содержит только нечётные гармоники:
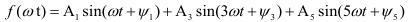
Кривые, симметричные относительно начала координат, не содержат постоянной составляющей и косинусоид. Такая кривая содержит только синусоиды (рис. 12.16):
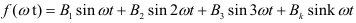
Кривая, симметричная относительно оси ординат, изображена на рисунке 12.1 г. Такая кривая не содержит синусоид. Она содержит постоянную составляющую и косинусоиды:
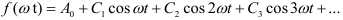
Эта страница взята со страницы лекций по предмету теоретические основы электротехники (ТОЭ):
Предмет теоретические основы электротехники
Возможно эти страницы вам будут полезны:
| Мощность трехфазного тока |
| Расчёт несимметричного треугольника |
| Несинусоидальный ток в линейных электрических цепях |
| Действующее значение несинусоидальной величины. Мощность несинусоидального тока |
