Для преобразования схем с идеальными источниками энергии используются приемы их эквивалентного переноса с изменением общего количества источников в схеме. Перенос идеальных источников не приводит к изменению исходных уравнений для контуров или узлов, составленных по законам Кирхгофа. Рассмотрим перенос идеального источника ЭДС (рисунок 3.22 а).
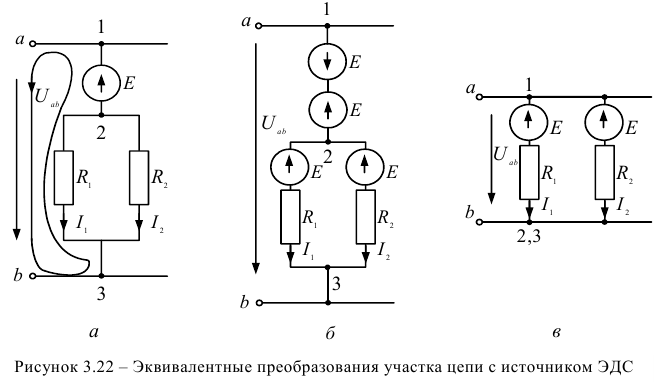
Уравнение по второму закону Кирхгофа для указанного контура имеет вид:
Для переноса источника ЭДС в ветви с резисторами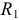 
и 
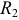последовательно с ним включают такой же источник ЭДС, направленный в противоположную сторону, а для сохранения уравнения, последовательно с резисторам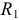и и 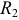включают такие же источники ЭДС, направленные вверх (рисунок 3.22 б). Последняя схема упрощается объединением узлов 1 и 2 в один узел, так как напряжение между этими узлами равно нулю (рисунок 3.22 в). Рассмотрим перенос идеального источника тока (рисунок 3.23).
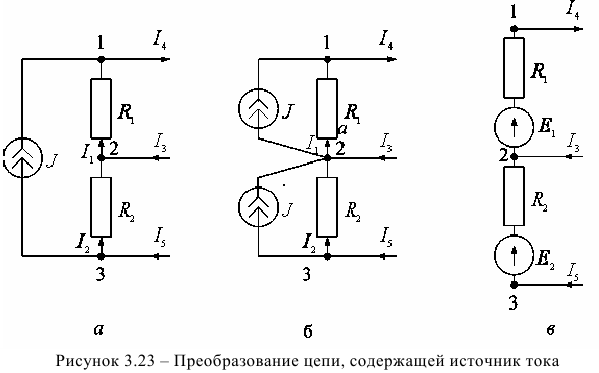
Перенос и преобразование цепи с идеальным источником тока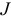 
в цепь с идеальным источником ЭДС 
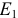и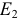 
.
Для переноса идеального источника тока 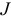параллельно с резисторам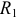и 
и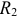 
включаются источники тока 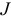, таким образом, уравнения, составленные по первому закону Кирхгофа, остаются неизменными для рисунков 3.23 а и б. Так для узлов 1, 2 и 3 соответственно, уравнения имеют вид:
Дальнейшее упрощение цепи выполнено заменой моделей источников энергии, содержащих источники тока (рисунок 3.23 б) моделями, содержащими источники ЭДС (рисунок 3.23 в), где: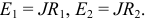 
Рассмотрим замену нескольких параллельных ветвей, содержащих источники ЭДС и источники тока, одной эквивалентной ветвью.
Участок цепи (рисунок 3.24 6) эквивалентен участку цепи, изображенному на рисунке 3.24 а, если ток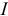и 
и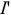 
равны и напряжения 
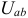и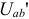 
равны.
Для схемы (рисунок 3.24 а) ток 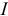можно определить по первому закону Кирхгофа:
где: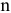 
— число ветвей с источниками ЭДС; 
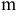— число ветвей с источниками тока; ток 
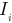— ток любой ветви с источником ЭДС. Расчет токов 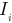выполним по закону Ома:
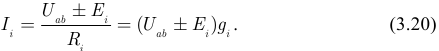
Следовательно:
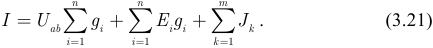
Для схемы (рисунок 3.24 б) в соответствии с законом Ома:
Равенство токов 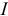и 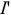в схемах (рисунок 3.23 а и 6) должно иметь место любых значениях 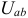, а это возможно только когда 
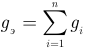и
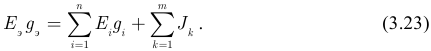
Следовательно:
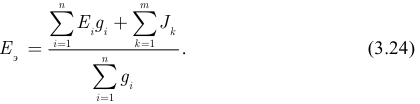
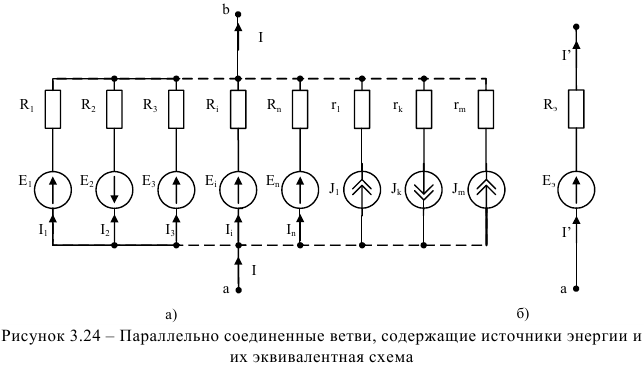
При вычислениях по данной формуле следует помнить: если ЭДС в какой-либо ветви схемы отсутствует, то соответствующее слагаемое в числителе выпадает, а проводимость этой ветви в знаменателе остается; если ЭДС в исходной схеме (рисунок 3.24 а) имеет направление, обратное току, то соответствующее слагаемое выйдет в числитель со знаком «-».
Задача 3.6.
Выполнить замену группы параллельных ветвей (рисунок 3.25) одной эквивалентной ветвью, если:
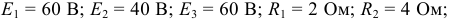
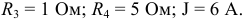
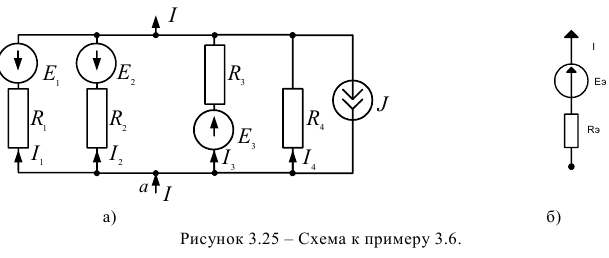
Решение:
Вычисляем:
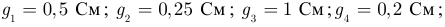
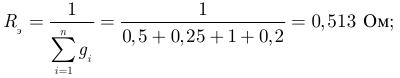
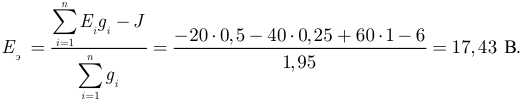
Параметры эквивалентной схемы рисунок 3.25 б: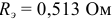 
и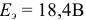 
.
Эта страница взята со страницы задач по электротехнике:
Электротехника — решения задач и примеры выполнения заданий
Возможно эти страницы вам будут полезны:
