Эквивалентность пар

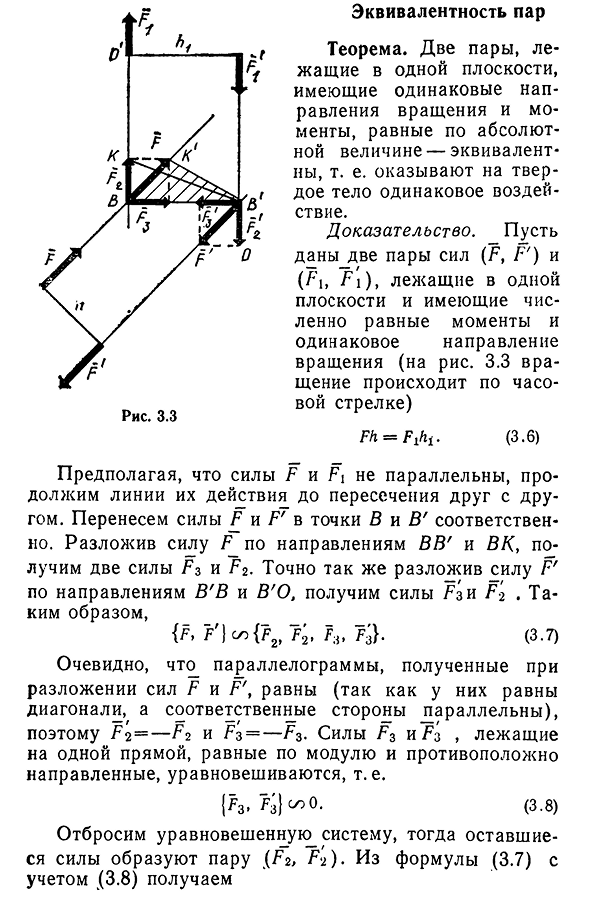
Эквивалентность пар

• Теорема эквивалентной пары. Две пары, лежащие в одной плоскости, имеют одинаковые абсолютные значения одного и того же направления вращения и момента, то есть оказывают одинаковое

воздействие на твердое тело. Приведем две пары сил, которые являются доказательствами (F, F’) и (L,F i), лежащих на одной плоскости и имеющих численно равные моменты и одинаковое направление вращения.) =(3.6)

Предположим, что силы f и L не Людмила Фирмаль

параллельны, и продолжим линии их действия до тех пор, пока они не пересекутся друг с другом. Переместим силы F и F ‘в точки B и B’ соответственно. Разложив силу F в направлении BB ‘ и VCU, вы получите две силы F3 и 7 2. Аналогичным образом, разлагая силы F

Ильин в в з з направлении это’о, Чтобы получить силу^Зи Ф2. И так оно и есть., {A~F2, F-l, F3}. (3.7) Поскольку ^ параллелограмм, полученный разложением сил F и F’, равен (так как они имеют равные диагонали,и каждая сторона параллельна), F2=—F2 и F3= — F3. Степени F3 и AZ уравновешиваются, индексируются на одну и ту же

• линию, равны противоположным, т. е. по модулю / G3,? z}s l0. (3.8) Отбрасывая равновесную систему, остальные силы образуют пару (A2, F2). Из уравнения (3.7) принять во внимание.(3.8), мы получаем 28|f, F) go{F2, f;). (3.9) теперь остается доказать эквивалентность пар (F2, F’2) и (L, F). Пара моментов (F,F’) численно равна квадрату, дважды

затеняющему DW/s,а пара моментов(F2, F2) дважды равна квадрату AV VC;но эти треугольники, следовательно, равны квадрату AV VC. Fft=F2ft1. (3.10)) Учитывая(3.6), мы имеем F2 / i1 = Fift1 (3.11) Или F2=F. Таким образом, силы F2 и L выводятся вдоль одной линии в одном направлении, т. е. сила F2 — это та же сила

L, которая передается из точки O ‘в точку B, а силы P’2 и Fi также одинаковы, следовательно, Людмила Фирмаль

формула (B2, F2) и co (Fi, Fi), данная формула (3.9), получим _ (F,? С Л(7р Ф «ручьи»). (3.12) Результат теоремы эквивалентной пары:1) Эта пара,не меняя своего действия на твердое тело,может быть перенесена в любое место на плоскости своего действия[здесь]. Движение пары в ее рабочей плоскости применимо только к твердому телу. Это свойство пары также может быть использовано для решения задач о равновесии тел, деформируемых внешними силами. Если такой объект считать твердым телом (принцип затвердевания), то это равновесие нарушать нельзя.

Смотрите также:

Предмет техническая механика 

Момент силы относительно точки на плоскости	Наука о сопротивлении материалов
Пара сил. Момент пары сил на плоскости	Мощность