Оглавление:
Экстремум функции нескольких переменных
Окрестностью точки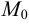 
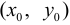будем называть множество точек плоскости, лежащих внутри некоторого круга с центром .
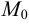Говорят, что функция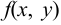 
имеет максимум в точке 
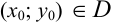, если для некоторой окрестности этой точки выполняется неравенство 
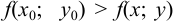. Аналогично функция 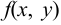имеет минимум в точке 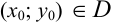, если для некоторой окрестности этой точки выполняется неравенство 
.
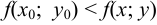Максимум и минимум функции носят локальный характер, их может быть несколько.
Теорема (необходимый признак существования экстремума):
Если функция двух переменных 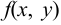имеет экстремум в точке 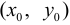, то каждая ее частная производная первого порядка в этой точке либо равна нулю, либо не существует.
Доказательство. Пусть в точке 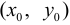функция 
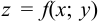имеет максимум. Это значит, что в некоторой окрестности этой точки выполняется неравенство 
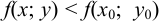. Будем изменять в этой окрестности 
, а 
зафиксируем положив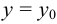 
. Тогда 
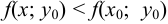и выполняется условие максимума для функции одной переменной. Поэтому либо 
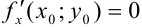, либо 
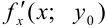не существует. Те же рассуждения можно провести для 
.
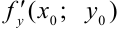Случай, когда 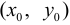— точка минимума, рассматривается аналогично.
Точки, в которых частные производные первого порядка равны нулю или не существуют, называются критическими точками. Таким образом, точки экстремума следует искать среди критических точек.
Задача №70.
Найти критические точки функции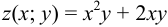 
.
Решение:
Найдем частные производные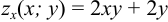 
;
Теорема. Пусть функция 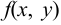определена и имеет непрерывные частные производные второго порядка в окрестности точки ,
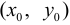которая является стационарной для 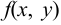, т. е. в ней 
.
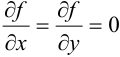Если в точке 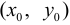разность 
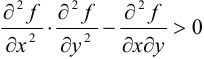, то она является точкой строгого экстремума, а именно строгого максимума, если в ней 
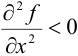; и строгого минимума, если в ней 
.
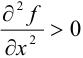Если же в точке 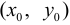разность 
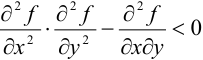, то экстремума в этой точке нет.
Наконец, если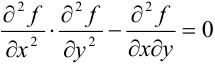 
в точке 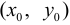, то экстремум в ней может быть, а может и не быть.
Задача №71.
Найти экстремум функции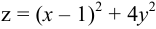 
.
Решение:
Определим стационарные точки. Для этого найдем частные производные и решим систему уравнений:
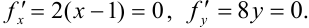
Точка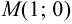 
является стационарной. Найдем вторые частные производные данной функции.
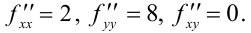
Так как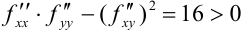 
и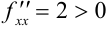 
, то данная функция в точке 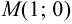принимает минимум: 
.
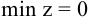Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
