Оглавление:




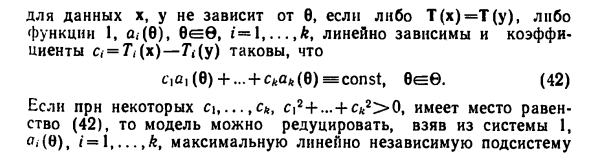



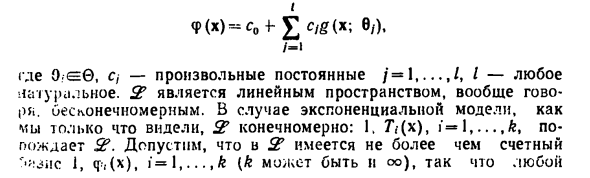

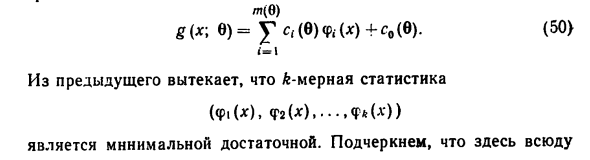




Экспоненциальные семейства, минимальная достаточность
- Рассмотрим непрерывную параметрическую модель (X, I, {Pb, ve61), где 6 ^ @, 0 „), k ^ 1, 0е /?», Плотность f e (x) meP ^ in определяется как: 145 / e (x) -A (x) exp (? 8,7, (x) + bF, 6)). С6) Семейство Po в этом случае называется k-параметрическим распределением. Экспоненциальное распределение (естественная параметризация). Некоторые важные семейства распределений после передискретизации После соответствующей параметризации была уменьшена до C6).
Настройки® X = P,% ~ — *, 7X = V lnx, -, 72 = V x {, для Прибытие на С6). Другой пример: независимая выборка из распределения Распределение; V (fi, o) имеет плотность связи 38 Экспоненциальная C6), 8i = -1 / o2, 82 = = с / о-. в Более общая форма экспоненциальной модели / в (x) -h (x) exp | y (8) 7, (x) +6 (8), C9) Где 6 = (8i …. lh), 8e0s /? ‘, На самом деле C6), естественная параметризация i |), = a, (8) Случай цветения. к
Например, Индивидуальные наблюдения в последовательности l независимых тестов Тест имеет распределение G (K; p) и плотность соединения равно η ;, … xn> 0 (см. B) §7) = (* 1 (…. xn) -1 exp (pJ1n *, — X? X (+ In (A «/ T (p)»)), C7) Людмила Фирмаль
Чтобы подтвердить это, ^ (8) на самом деле exp (& (8)), так что a, F), i = l, …, k функции С9) служит нормализующим фактором. Обратите внимание на то, что мы ресэмплируем экспоненциальное распределение ns Экспоненциальный тип также принадлежит к этому типу: 146 (Xl! |, X’2 ‘x «‘»)) = X Следовательно, в примерах С7) и С8) Только когда n = 1. в Из теоремы факторизации при дополнительных ограничениях A6), A7) Это векторная статистика T (x) = G | (x), …, , .., Γ * (x)) достаточно для модели C6). OG- Пределы A6) и A7) являются избыточными и широкими Понимание достаточности.
Интерес, как п в дискретных моделях Предоставить достаточную статистику для сокращения данных Наибольшая степень. Достаточно статистики S (х) называются Достаточно минимальная статистика, если она может быть представлена (Вектор) Функция достаточной статистики. Свяжите достаточно разделов с достаточным количеством статистики T (x) 95 комплектов: i: T (x) = t | Д0) Минимальная статистика S (x) является достаточным минимумом Достаточно разделов имеют достаточно элементов Разделы содержатся в наименьшем элементе. {x: T (x) = t} s = {x: S (x) = st}.
- Самые маленькие разделы, как дискретная модель, При определенных ограничениях они формируются из эквивалентных классов, Эквивалентность по R: х / б? у? = * / e (x) / yy) не зависит от c. D1) Подтвердите это утверждение экспоненциальной моделью C9). Более чем Во-первых, обратите внимание, что плотность C9) исчезает Общее множество {x: A (x) = 0}, таким образом Рассмотрим все такие хз. Тогда соотношение / в We (Y) exp (? a, (e) G \ (x) -7 \ (y)) j 1 1 = 1
Для заданного x T (x) = T (y) или Функции 1, o, — (c), wave, 1 = 1, …, * линейно зависимы и имеют коэффициенты Коэффициент c = 7 \ (x) -7 \ (y) равен 0 «= 0. D2) Для некоторых c1, …, ck, Ci2 + … + cft2> 0 prn, Уравнение D2), модель можно уменьшить, взяв из системы 1 Мб), <= 1, ..,? Крупнейшая линейно независимая подсистема J.iMeiniB в C9) остальные функции a, @) в линейном представлении Производительность по этой системе. Таким образом, 1, а, @), i = l, k линейно независимы. В этом случае раздел Класс эквивалентности для D1) совпадает
Достаточно статистики S (x) ) D3) По теореме разложения, если S (x) = S (y) = s, / e (> 0 = gi (s; 6) Mx), / e (y) = g1 (s; c) A1 (y) И для всех 0e6 таких, что gi (s; 0)> O, соотношение Независимость, т. Е. T (x) = T (y) Установить. да D3) В таком мини Минимальная статистика S (x), удовлетворяющая ограничению A6), A7) и, следовательно, утверждение о минимальности T (x) Проверено только в этом классе статистики. В примере C7), C8) Требования А6), А7) выполнены и достаточная статистика Я л [р л \ Y lnxt, Y ^ xt) и! ^ Л | 1 $ J * » ‘- минимум / = | 1 = 1 * = 1 / = | Для образцов с распределениями G (K; p) и N (n, a). Для линейной статистической модели с нормальными наблюдениями Наблюдаемое значение B7) Статистическое значение B9), коэффициент 6 и Для A2 достаточно наименьшего минимального значения.
Достаточно раздела D0). Указывает, что этот раздел самый маленький Минимум. Людмила Фирмаль
Равномерное распределение при @. 6) (см. Пример (II)), выставка Экспоненциальное распределение с параметром шкалы сдвига ( (Пример (плохо) Y не принадлежит экспоненциальному семейству. Характеристики этих распределений следующие: Установите места, где плотность распределения не равна нулю (Грузоотправитель) зависит от параметра, В C6) поддержка всех распределений одинакова- {x: / i (x)> > 0} Однако минимальности, рассмотренные в Примере (II), (Iii) Тот же вывод доказал достаточную статистику Вывод, экспоненциальная семья. то же Выводы относятся к цензурированным образцам Пример (IV). |
Чтобы построить достаточно минимальный раздел n Другой подход. Как дискретная модель, Следующая статистика будет генерировать достаточно расколов Boom: L (r. \ C), f ° (x). в ев 148 Зависит от 8 как параметр, достаточно минимального значения Разделы генерируются функциональной статистикой L (x; 9) / L (x; in); vev, D4) В предположении, что каждый перевозчик имеет такой дальний взгляд Измерение включено в перевозчик Pgo. D4) удобнее, если все основные опоры Pe совпадают. Перейдите к логарифму. InL (x; c) —InL (x; b) =? (X; c), 8 <= c. D5) Считайте, что этот подход экспоненциальный Модель С9).
Подстановка f (x) из C9) и D5) дает: г (х; с) =? (O1 (c) — ^ (c,) O’4 (x) + F (c) -6 (b)), сеть D6) 1G.1 Поэтому раздел X генерируется путем сбора статистики Статистика D5) в этом случае соответствует разделу, сгенерированному Статистика вектора T (x) = G * 1 (x), …, Tk (x)), Достаточно, если это уже проверено. таким образом Следовательно, экспоненциальная модель C9) может уменьшить минимум. Минимальная и достаточная функциональная статистика D5) До L-мер Вектор Т (х). Экспоненциальная функция Экспоненциальная модель C9) Функциональная система 1, a, -F), i = \, …, k, веб-съемка Линейно независимы, так что вы можете легко понять, что вы можете выбрать Значение 8 (|) ev, i = l, …, k.
Следовательно, матрицы [a, (b (/)) — a, (bo), i, j = l, …, k] невырождены и соотношение D6) 7 «((x), i = lk, Функция 1 может быть выражена линейно относительно g (x; 8 (/)) i / ффт Любая непрерывная модель (77 ,,, = 6}), все основные совпадения поддержки Pe. рассматривать Вы считаете пространство 2? Все виды конечных линейных комбинаций Комбинация: ; /). Еда 0: ^ @, c -, — любая константа /=1,…,/, I-любая Естественный. S7 вообще линейное пространство Говорят бесконечные размеры. Для следующей экспоненциальной модели Как вы можете видеть, & является конечной размерностью: 1, 7 \ — (x), i = 1, …, fe, by Ты ждешь 9?
Предположим, что существует не более 2 * «U’Mls. i, φ, (x),] ‘= 1, …,? [k, может быть, o) так 149 Представляет элемент f (x) e21 в виде конечной линейной комбинации Сочетание основных элементов: В частности, это относится и ко всем функциям g (x; c), bev. В этом случае 6-мерная статистика ( (x) = g (x; b) =? U (b) cf, (x) + b (b), Я Откуда f (x) = f (x) exp (? at (c) (p, (x) + b (c) |, D8) То есть статистическая модель является экспоненциальной. так Таким образом, м перевозчик Экспоненциальная функция пространства SB В конечных размерах. | Рассмотрим, что дает подход, описываемый независимой моделью Индивидуальная плотность fB (x), независимая повторная выборка для 6e9
Наблюдения сосредоточены на одном наборе. делает g (x; 0) = 1n / in (x) -In / in (*), в e 0, D9) И 2 «- линейное пространство функции (p (ds). Линейная комбинация системных функций D9). предполагается, что 1, ffi (x), i = 1, …, k (k может быть равно oo) является основой 2 «. Любой 8е0 т (с) g (x; c) = yn, (c) φ, (dg) + c, (c). E0> Из предыдущей 6-мерной статистики Минимума достаточно. Здесь везде х — скалярная переменная. Потом опять Объем независимой выборки n. по-видимому N g (xn; c) =? g (* ;; 6), 9se, И с е0) pt (c) g (xn; c) = y (Yct @) φ, (,) + с0 (в), = t (c) p = 2 с, @) j; φ, — (deu) ¦¦; В этом случае 6-мерная статистика W> i (x „) …, ¦» (xj), ifc (x „) = VΦ | ( /), i = lк, E1)
Минимума достаточно. Если размерность k статистики E1) конечна, то при n> k Обеспечивает сокращение данных по сравнению с достаточно тривиальным Достаточно статистики-вариации ряда. Делая так, D8), распределение отдельных наблюдений, и Вся выборка принадлежит экспоненциальному типу. Тем не менее, Условие k n, вы можете получить следующее утверждение: Вы не можете уменьшить размеры статистики в достаточной степени. На самом деле, в этом случае статистика ^ \ (xn), …, r | zl (xn) Якобиан d (Hf \, …, ^ n) l, потому что он функционально независим /g(x1,…,xn) — это набор «» = {xn: x, eE, и-л …, н).
Следовательно, существует интервал AeD. Подмножество ^ сгД Определенно рассмотрим х „, учитывая, что 151 * == 4) «CJcti>» •••. Если * («)) также является уникальным, получается связь. Решение для * (i>, …, * (解), поэтому в некоторых доменах E «переменные XI, …, XN (это Каждый bev) stats (.vA), ….. v (n>) эквивалентны stats (Ti (* (! >> ••• .. ((>) Ch’l (* и> …., l ‘(, ())). Раздел, который генерирует ряд вариаций в области D, То есть (jc (i>, …, * <«>) — минимум По крайней мере, достаточно статистики в области D. Докажите приведенное выше утверждение для функции Функциональная независимость статистики я (хп) г | 4 (хп). до
Давайте скажем обратное. Потом якобиан = det [c4v (xri) / <3.v /> i, / = 1 с] = det [v’i (x,), i, / »1 с] E2) D «= {xn: x, -e D, i = 1, …, n} равно нулю. Это противоречит линейной независимости системы 1, <pi (x), …, φ * (x). Действуй по индукции. Если s = 1 (P ‘, (xi) == 0, cp, (*,) == const получают противоречие. Предположим, что d (^ u —, ^ s-i) ld (xu …, Xs-iL ^ 0. Затем разверните определение и E2) Определитель, последний столбец, xne.V Ais (f’i (xs) + … + Ass (ffs (Xs) ^ O, E3) Где AjS = AiS (xi, …, xs- ) является дополнением к соответствующей алгебре Соответствующий элемент определителя E2). По предположению Индукционная гипотеза Тогда есть значение x ° a-j-i. «A ° s — Ass (x ° * s_i) ~ дф. В этом случае получим от Е3) + Asi (fs (xs) -const, A ^ φ0, несовместимо с линейным Линейная независимость функций
Смотрите также:
| Достаточные статистики в дискретной модели | Полные достаточные статистики |
| Определение достаточной статистики, теорема факторизации | Наилучшие несмещенные оценки в дискретной модели |
Если вам потребуется помощь по статистике вы всегда можете написать мне в whatsapp.

