Оглавление:


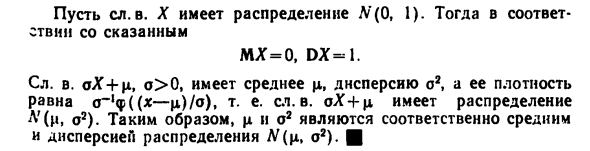


Экспоненциальное распределение
- Экспоненциальное распределение с плотностью У.е ~ е, х> 0, является частным случаем гамма-распределепия с параметром формы, равным 1, и обозначается G (k, 1) .Из леммы 1 вытекает, что сумма п независимых С (а, ^ -распределенных ел.в. имеет распределением G (X, n). сг.о-обом (§ 5. лемма 2). Среднее и дисперсия экспоненциального рги-и; / *> делс1ш>! О (к, ) равны л1 и ?.
~ 2 соответственно. плотность ф (х) = сэ * ‘/ г, -оо <х <+ оо, где константа с = 1 / У2л находится из условий нормировки: + 00 1 = J - О.Б. 00 1 о Людмила Фирмаль
- Нормальное распределеиие с плотностью обозначим через N (\ i, о2). в соответствии с правилом, будет обозначаться <р (х), а соответ- представить ф. р.- Ф (х). N @, 1) нечетного порядка, очевидно, равны нулю, а четного- .? „УгА- L / я J / я о Принимая во внимание формулу Г (р + 1) = рГ (р) и получить рекуррентное соотношение откуда для центрального момента порядка 26 BА — 1) B * —3) -…- 3-1.¦ (9) Сть ел. В. X имеет распространение Л ‘(О, 1). в соответствии со сказанным МХ = 0, ДХ = . Xл. В. AX + \ i, о> 0, имеет среднее значение, дисперсию о2, а ее сигнал означать ~ ‘<р ((х — ц) / °) «т-е-с11-в. оХ + и имеет распространение L ‘(ц, о2). и дисперсиеП распределении N (\ i, о2). ¦ 53
Лемма 2. Пусть X, -— независимые ел. N (\ n, о, 2), 1 = 1, 2, …, п. Тогда ел. В. Х (+ … + Хп имеет распре- доля N (\ ii + … + \ i ,,, О | 2 + о22 + … + о, .2). Положим У, = (Х, —ц) / о, и запишем В. У | + а} ‘г, а -Аг / ои имеет долю # @, 1 + а2). Проведем преобразование показателя экспонентов в интеграле A0): • * ‘- (У-vJ / a2 = -V2 (1-i-4 «) -2×0 -т а- \ а- у а *
Подставляя A1) в A0), получите, что _ ± (J! _) -. ± к1 где 2л — М очевидно, не зависит от тебя, т. е. является постоянной. A2) с (8), получить разрешение. Людмила Фирмаль
Смотрите также:
| Оценивание по первым г порядковым статистикам | Распределение х2 с п степенями свободы |
| Гамма-распределение | Доверительные оценки для н и о2, когда один из параметров известен |

