Оглавление:
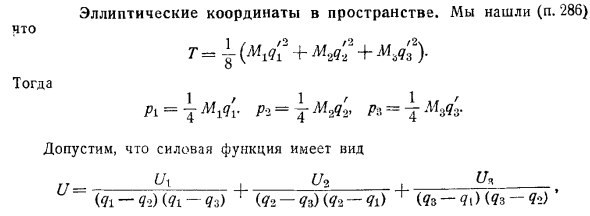



Эллиптические координаты в пространстве
- Мы обнаружили, что Н.286 Т = + L42 2 + L4a 2 нашел. И затем… A = 7 A A = 4 W3 3. Предположим, что силовая функция имеет вид У = р 2 71 Т з 2 2 з 2 2 з я зз, где ИП является функцией только переменных Q только и от3 переменный 3 м квартале только. У нас есть Я L 3 и Их значение пункт 286, то уравнение А 2. Случай = 2 около 1 21 Заменить на Alj.
В случае, когда отталкивающая сила пропорциональна расстоянию, а точка вначале лежит на кривой С и не имеет начальной скорости, обратить внимание на вид закона движения и выражения натяжения нити. Людмила Фирмаль
Это выглядит так: m , m3 G LF1 dW 2 1 1 Л 4 42 4 4з d4i J 1 42 Ф 42 ДГ ч 7 я ty2 7 е dW Г Чл— 91 З ч5 ддя Дж Для значения постоянной константы, согласно Якоби, найти полный Интеграл этого уравнения при допущениях, сделанных относительно U, уравнение 2а+2р 1 + 2а+2р 7а+Л 4 2а+2 9з+ ЦУ Я. Два 1 2×1 9 7 ЗН 2 Я + ХГ 41.ЧС 41 = ч является рациональным числом по отношению к общей м функция остатка 2Д 2У + У2 4 41 4 4 4z ящика Равен A. тогда уравнение W при замене A на эту формулу можно записать следующим образом: + 41 4z Chr 41. 2M4N 1 4з 4i 4з = 0. Это уравнение, очевидно, имеет Интеграл У7 = 42 + Куда 2sf по = 2aJr2 qidrh фут интерфейса = 1,2,3.
- Фактически, эта формула гасит каждый из 3 членов частного дифференциала Equation. To найдя орбиту, мы приравниваем частные производные W по отношению к a и p: f d4l с константой a и p. Д dq2 + с Д4 J VS. fiq J VS2f q2 J VrSjW f 41 d4i. 4id4i, D 4z d4i R J 1 41 Vs2f q2 J VStf qt В некоторых случаях, когда нет сил, то есть эти уравнения должны представлять собой прямую линию пространственных эллиптических координат. Они называются qlt q. B соответствует 2 алгебраическим отношениям между q3.Это первое обобщение результата Эйлера, показанного в конце предыдущего упражнения, и частный случай теоремы Абеля, примененной к суперэллиптике 1 го класса integral.
Материальная точка, вынужденная двигаться по окружности, притягивается или отталкивается одной из точек этой окружности. Людмила Фирмаль
Сроки, вы можете получить его, сравнив L. Полярные координаты гиб движущейся точки в функции времени. Выразить координаты точки в функции времени и вычислить ускорение. которой б — 0. Отсюда непосредственно найдутся х и у в функции времени. При движении твердого тела плоскости, перпендикулярные к траекториям точек, лежащих в одной плоскости, проходят через одну точку. соединяющим проекции точек на эту же плоскость с точкой ее пересечения с центральной осью. Построение мгновенной винтовой Оси по Понселе. точки. неподвижной оси. Найти для этого тела мгновенную винтовую ось, неподвижную линейчатую поверхность и подвижную линейчатую поверхность 15. Показать, что в этом движении все другие точки тела описывают эллипсы.
Смотрите также:
Решение задач по теоретической механике

