Оглавление:
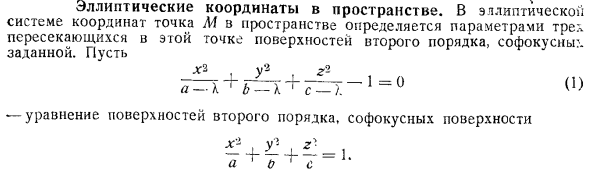




Эллиптические координаты в пространстве
- В эллиптической системе координат точка L1 в пространстве определяется параметрами 3 х криволинейных поверхностей, пересекающихся в этой точке, и задается конфокально. Позвольте мне. Х3, V2 и Т Р2 к + РБ + м м 0. Уравнения квадратичной кривизны, конфокальной кривизны + г +. в 1 е 1. Если вы поставите A b c для уточнения, то уравнение X c 1 представляет собой фактический эллипсоид, b X c представляет собой. Гиперболоид одной полости, a X b представляет собой Гиперболоид 2 полостей и, наконец, в случае X a виртуальный эллипсоид. Такие 3 конфокальных поверхностей проходят через каждую точку пространства.
На самом деле, если Х, У, Z рассматриваются как заданную величину, тогда уравнение 3 го порядка относительно x 1 имеет 3 действительных корней, 1 из которых будет меньше, чем C, еще 1 находится между C и B, 3 й между B и A. Это можно проверить, подставив значения x, показанного в левой части уравнения, и знак на левой стороне определяется в следующей таблице. e очень маленькое положительное число. Значение параметра X………— Есть еще совпадающие символы Часть Формулы 1……… 4 Трассировка……………. К2 с + т ч б + д С я 4 00 Эти 3 маршрута представлены QB q2r q3 в порядке убывания значений.
Так как большая ось орбиты кометы очень велика, то эта близкая к Солнцу часть орбиты почти такая же, как если бы большая ось была бесконечной, т. Людмила Фирмаль
Для X = 4iu получаем 2 гиперболические поверхности, для X = 73 получаем 1 гиперболическую поверхность, а для = q3 получаем эллипс. Как известно, эти 3 поверхности ортогональны друг другу. Например, 2 поверхности Один икс. УЗ ЗЗ г Б 2К Зет с К2 1 = 0 Поскольку условия ортогональны, то ортогональны длд г ДХ дх ду ду ДЗ ДЗ Метод непосредственной проверки этого совпадает с выражением ЯГ. 3 величины qv q2, q называются эллиптическими координатами точки M x, y, r.
Чтобы представить декартовы координаты x, y, r в q2, q3, заметим, что qlt q2, q это 3 корня уравнения 1 относительно X. И так оно и есть. Х У2, Р8. 71 б Г Х Х а— б— х — К А Х М Х с х Х 1 х Г2 х Три Икс Если вы умножите обе стороны этого тождества на a Xi и установите X = a, вы получите: Д ч Б А С а, а также = Б 91 яд 9Н 7 С Б А Б Цзы с яд к К2 к К3 А С а с Вычислите уравнение AS2 в этой системе координат.
- Если мы возьмем логарифмический дифференциал обеих частей уравнения выше, мы получим: 2dx ЯЯх1 9, dqa 7З Х 7и В2 а 2dy dqi, dq ДК Г 91 72 я б 2dz i4i, 9, dq3 Z с 72 с работы с 7z с Для 4ds, получить выражение следующего вида 4 dx2 + dy2 4 dz2 =Mt dq2 4 Л12dq2 dq Р Dqxdq2, потому что поверхность ортогональна… Нет никаких условий. Легко проверить соотношение 2 узла а а 72 + Б Ц Б М с Т с В2 Это указывает на то, что dqx DQ2 имеет нулевой коэффициент.
Значения значений M2, M3 являются: ЛУ2 з М1 = 1 а 2 + Г Д 2 + м с Относительно X и этой перестановки возьмем производные обеих сторон тождества 2 Я понял, что я выжил X = qv и в результате 2 й части мне не нужно их вычислять, так как те, которые содержат фактор X qlt, исчезают. М У1 1 91 Где f X обозначает произведение x X X c X. таким же образом м = 2 Ф 4z ящика Тогда все участники 7н В частности, учитывая кривую СХ пересечения 2 поверхностей дуги 75 = const, а q3=: const рис. 174, дифференциальный dsx этой дуги равен dq2 dq3 = 0. Отсюда 1 = 4 Ми дисквалификацией. Аналогично, вы показываете дуги кривой C в ds2 и ds3 И вдоль C3, поверхность qt const.
Он только предположил, что в то время как планеты описывают лежащие почти в одной плоскости эллипсы с малыми эксцентриситетами кометы описывают очень вытянутые эллипсы, лежащие в произвольных плоскостях. Людмила Фирмаль
Пересечение, q3 const, и поверхность qx = const., 2 = Конст. В свою очередь, дугу ds любой кривой можно рассматривать как диагональ коробки со сторонами dsb ds2, ds3. Значение t выражается как Кроме того, уравнение Лагранжа может быть легко создано. Форма левой части этих уравнений очевидна, поэтому она ограничена определением правой части. Разложим силу F на 3 составляющие Fb F2 и F3, соответствующие кривым Cb C2 и C соответственно. Предполагается, что эти компоненты положительны в направлении движения точки M вдоль каждой из этих кривых, при этом только увеличивается 1 эллиптическая координата и сохраняются 2 другие константы.
Сообщите точку M смещения, где 0s и 0s являются постоянными, а 0t, вероятно, увеличится на 01.Тогда возможная работа силы F будет равна b0 с другой стороны. С другой стороны, Силы работы Fo и A3 равны 0, поэтому в этом случае силы работы F равны Поэтому мы имеем g, UlG, 1 2 Рисунок 175.
Смотрите также:
Решение задач по теоретической механике
| Интеграл кинетической энергии | Эллиптические координаты в плоскости ху |
| Сферические координаты | Уравнения Лагранжа для свободной точки. Упражнения |

