Оглавление:



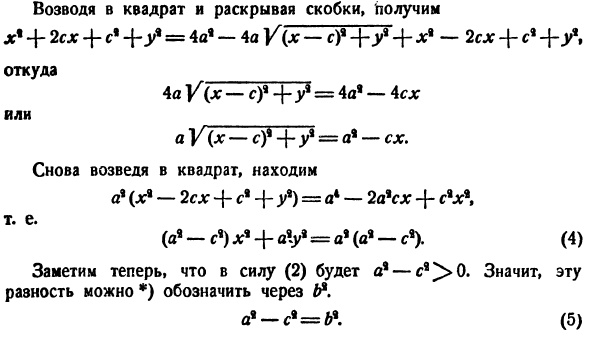










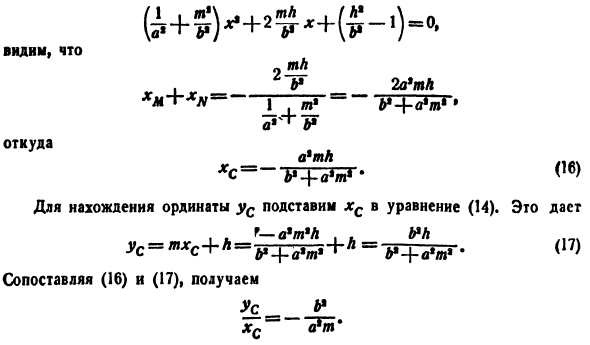


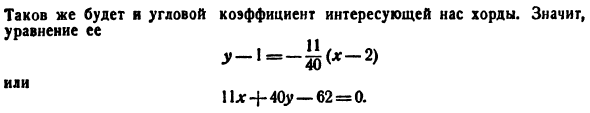

Эллипс
- Эллипс При рассмотрении линии в уравнении естественно размещать линии в соответствии со сложностью этих уравнений. С этой точки зрения прямую линию следует считать самой простой линией. Это потому, что в этом уравнении есть первая сила. Ниже приведена строка со степенью уравнения 2-го порядка, с точки зрения сложности. Есть 3 таких линии (они называются кривыми 2-го
В этом разделе, вы узнаете про эллипсы. Н°1.Определение эллипса. Его стандартное уравнение. Представьте, что в стол вдвинуты 2 гвоздики, а их концы перевязаны ниткой длиннее расстояния между гвоздиками. Натянув этот поводок мелом и направив этот мел на стол, он рисует на столе замкнутую
порядка*): эллипсы, параболы и гиперболы. Они играют огромную роль в математике, науке и технике. Людмила Фирмаль
овальную линию. Эта линия называется эллипсом. Расстояние от точек, движущихся по овалу до шпилек, меняется, но их сумма всегда будет равна длине шпагата. Далее мы переходим к точному обозначению вопроса. Определение эллипс-это линия, представляющая геометрическое положение точки, сумма
расстояний которой от 2 обозначенных точек, называемых фокусом, является постоянной величиной. Фокусная точка эллипса представлена F и F%, а сумма расстояний от точки эллипса до фокусной точки представлена 2a. тогда для любой точки M на эллипсе (рис. 40)、 MF + MF = 2a. (1) Расстояние между фокусами эллипса обычно обозначается 2а. FF = 2 секунды. Потому что 1 сторона треугольника всегда короче, чем сумма других 2 сторон、 (2) * )
- Круг — это круг, уравнение которого (x-b) » +(y-by = /?■Поскольку существует степень 2, это также кривая 2-го порядка. Однако ниже вы можете увидеть, что окружность является специфическим видом эллипса. ω можно определить следующим уравнением: 2 например, уравнение y-x = 0 можно записать в эквивалентной форме y-2uh + x * =
* 0.In текст, когда мы говорим о 2-й строке, мы имеем в виду кривую. Чтобы вывести эллиптическое уравнение, необходимо сначала выбрать систему координат. Нарисуйте ось Ox Это определяет положение оси Oy (рис. 41). ясно, что в этой системе фокус имеет координаты F(c, 0) и F(-c, 0).Для любой точки M (x, y) равно МФ = V(х-с)* — {- г \ СЧ = V(х + с) * + у . Из этого и(1) ясно, находится ли точка M
г(х-с) + у * + г(х + Су -} -/ = 2а.(3) Людмила Фирмаль
выше эллипса, в зависимости от того, является ли уравнение истинным или ложным. Таким образом, уравнение(3) является уравнением эллипса задачи. Это уравнение довольно громоздкое, но оно может быть simplified. To сделайте это, перепишите (3). Когда скобка возведена в квадрат
и открыта, X1 +2сх + с * + у = 4а9-4A V (X— c) 9 + / + * 9- 2с* +C4 откуда получается. 4а V (х- = 4a9-4С * Или И V (ДК-с) * + у9 = А9-СХ. Квадрат снова и найти А1(л: 9-2sdg + С9 + г)= А4-2lvcx + с%х \ Иначе говоря (А9-С9) Х9 + эВ = А9(А9-С9). (4 )) (2) Обратите внимание, что из-за a9-c9}> 0.So эта рая может быть представлена следующим образом*) А1-С * —
С(5) (4) принимает форму РХ * — \ — АУ% = деление на * б \ у * б\сделать наконец * От\ Это самый простой (или стандартный) эллипсоид equation. It полезно запомнить пропорции Мне. с. * Эквивалентная(б). н°2.Изучите форму эллипса. Мы изучаем форму эллипса, опираясь только на уравнения Решение этой задачи начинается
с установления следующей теоремы: эллипс теоремы симметричен относительно оси Oy. Доказательство. Возьмем 2 точки M и L1, симметрично расположенные относительно оси Oy (рис.42).Если какая-либо из точек M9 N принадлежит эллипсу (6), то доказывается теорема, указывающая, что неизбежно и другие точки будут принадлежать этому эллипсу. Быть ясным、 начальные
координаты от (p, q).Рис.42.Тогда координаты Метрической точки Н ( -/?и Q) будет. То, что точки M (p, q) находятся на прямой (6), можно записать в виде уравнения. Тот факт, что точка в прямой (6) pt q) доказана, записывается в виде уравнения. Итак, зная, что (7)истинно, необходимо указать, что (8) истинно. И это совершенно очевидно. (=РК (9) Это доказывает теорему. Н м т АА 1 —— Т 1 1 к 1 1 | Р О Р х Замечание. Если мы рассмотрим это доказательство, то увидим, что оно основано на том факте, что равенства (7) и (8) истинны или ложны одновременно. Последняя ситуация аналогична уравнению(9), а уравнение(8) (7) из p *(- pf).Это связано с тем, что
он получается путем замены на (- p) k = pA. Линия B * 1 Он также симметричен относительно оси Oy. То же самое относится и к линии 5jc *-9 x * y + 3 * Y = 42 И так далее. Что вообще важно, так это справедливость. Принцип симметрии. если координата x входит в уравнение произвольной линии только с четной степенью, то эта линия симметрична относительно оси Oy. учитывая, что координаты X и y полностью равны, ясно, что кривая уравнения, содержащая только ординату y в уравнении, симметрична
относительно абсциссы. В частности, эллиптическое уравнение (6) содержит только y. следовательно, эллипс симметричен относительно оси Ox. Учитывая вышесказанное, при установлении эллипса распознается форма всего эллипса. Вид детали по 1-й координате angle. To для этого решите уравнение (6)
относительно y*). Рисунок 43. Далее последуют 4 заявления. 1) если x = 0, y = B. 2) Когда x увеличивается, y уменьшается. 3) Если x = a, y = 0. 4) в случае x вы можете видеть, что y-мнимое число. То есть эллипс(6) вообще не имеет точки x> a. То есть, когда x увеличивается от нуля до a, ордината y уменьшается от b до нуля. Поэтому часть эллипса
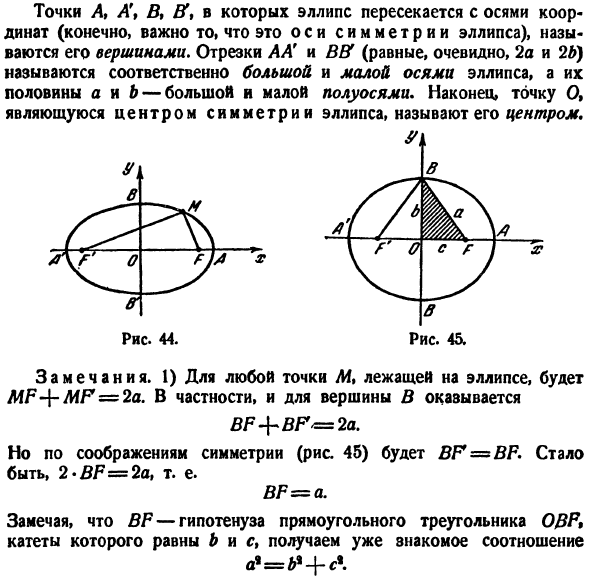
при первом координатном угле имеет вид, показанный на рисунке 3.И весь эллипс показан на рисунке 43. 44. Точки, в которых эллипс пересекает координатные оси A \ B, B% (важно, конечно, что это оси симметрии эллипса), называются его вершинами. Отрезки AA ’и BB(по-видимому, равные 2a и 2b) называются соответственно
большой и малой осями эллипса, а половина из них a и b называются Большой и малой осями. Наконец, Точка O Замечание. 1) для любой точки M, которая находится на эллипсе, MF — {- MF = 2a. In в частности, для вершины B、 БФ + БФ < = 2а. Однако по соображениям симметрии (рис. 45) BF == BF. So, 2 * BF = 2a, то есть БФ-а. БФ приобретает привычное соотношение, отмечая, что ножки
являются гипотенузой прямоугольного треугольника ОВР, который равен В и С. 2) круг можно рассматривать как эллипс, в котором фокус заключается в том, чтобы match. In в этом случае c = 0, следовательно b = a, и выражение (6) принимает вид: л * о * То есть, это будет хорошо известное уравнение окружности вокруг начала координат: х * + г * = в \ Образцы. 1) Найти эллипс, где расстояние между длинной и короткой осями равно 6, а фокусное расстояние
равно короткой оси. Каковы условия задачи? Ва%+ б * = 6Т 2В = 2В 2-е отношение дает c = b%.So,= + тогда a * = 2b.So это\ ’ bb%= b и 12.Тогда A% = 24, и Эллипс Вот оно. 2) найти длину овальной хорды (6) через фокус перпендикулярно главной оси. Верхняя часть интересующего вас кода (M y0).Длина аккорда равна 2y0.С другой стороны, jc0 = s. так как (Почему?) Затем т е) — у? — Т. а * т ^-«т. е.% я » Откуда 2 года » = 2±\
П°3.Овальный, как сжатый circle. It легко представить себе форму эллипса, сравнивая уравнения £ + £ = «00 В уравнении круга х * + г * = а (12) Диаметр-это большая ось эллипса (рис. 46). Пусть M и N-точки эллипса и окружности с одинаковыми абсциссами x. каждая вертикальная координата показана в виду и yc. To будьте ясны,
предположим, что обе точки M и N находятся на оси O*. (Из I)и (12)、 Рисунок 46. Поэтому、 х * 9 Вы можете видеть, что ордината каждой эллиптической точки получается умножением некоторого числа на ординату соответствующей (т. е. имеющей ту же самую абсциссу) точки окружности. Это число (одинаковое для всех точек
эллипса) меньше 1 (потому что Полученный результат выражается тем, что эллипс (11) берется из окружности (12), используя сжатие во времени (Примечание).Сжатие б \ Это y, и-не то время! Или, короче говоря, что эллипс сжат Х%В1 Круг. Например, эллипс, полученный из окружности = 36 компресс используется 2 раза(потому что здесь a
= 6 Б = 3). в N°4.Эксцентриситет эллипса. Определение эксцентриситет эллипса-это отношение фокусного расстояния к главной оси, то есть число И С тех пор об эллипсе 0 И мы рассмотрим ряд аккордов, которые параллельны этому диаметру. Найдите геометрические положения их средних точек.
Решение. Сделайте угловой коэффициент диаметра f — / равным m. выберите строки, параллельные диаметру. Уравнение этого аккорда является у = х + н. (14) Мы знаем, что нам нужно решить уравнение (13) и (14) вместе, чтобы найти точки M и N, где выбранный код пересекает эллипс. Если подставить y из (14)в (13)、 Абсциссы XM и xN в точках M и LG являются корнями этого уравнения 2-го
порядка. Мы заинтересованы в середине кода МН с(ХС; ус).По известной формуле Год / ПА V) L Я XC-5 * рисунок 48. Поэтому вместо того, чтобы брать корни формулы (15) отдельно, нам нужна сумма этих корней. Но сумма корней квадратного уравнения Ах * + Ьх + С = О В equals-записать выражение (15) в следующем формате Посмотреть на это. 。 — Оказывается, 2а ’ Тл XM-TXN-1 t * M + A «’* Откуда эф » а Чтобы найти ординату, подставим DGs уравнения (14). это даст А-а. 。 РН уя = mxc по + ч ^ ljrF— + ч = г + fltm>. (17 ))
По сравнению с (16)и (17)、 Мы Это означает, что точка С находится на прямой линии. Очень важно, что формула (18)не содержит числа А, которое отличает другие аккорды семейства от выбранного нами. Таким образом, средняя точка всех аккордов семейства находится
на линии(18).Эта линия проходит через центр Ellipse. So, желаемым геометрическим местом является прямой отрезок (18), который содержится внутри Oval. In другими словами, это геометрическое место является диаметром эллипса, а угловой коэффициент
m *этого нового диаметра II-II равен (19) Диаметр II-II называется сопряженным диаметром/ -/. Если диаметр теоремы II-II сопряжен с диаметром 1-1, то диаметр 1-1 сопряжен с диаметром II-II, То есть эти 2 диаметра сопряжены друг с другом. Доказательство. Принять угловых коэффициентов диаметра я-я н в II-//равна м,
соответственно, так что М * знак » + » обозначает угловые коэффициенты сопряженных диаметров второй-второй. Согласно (19)、 Б * Т * * = а * т * ’ Но в итоге m +представляется m по той же формуле(19)… Таким образом,=доказывает теорему. Замечание. Если малая ось эллипса равна 1 диаметру, то длинная ось того же эллипса является его сопряженным диаметром. Это означает, что ось
эллипса является взаимно сопряженным диаметром, перпендикулярным друг другу одновременно. Если эллипс является окружностью, то конъюгат 11 — / / диаметра/-/всегда будет перпендикулярен этому концу. Для эллипсов, отличающихся от окружности, 2 диаметра, сопряженные друг с другом,
за исключением осей, больше не перпендикулярны друг другу. Действительно, согласно (19) т.* — к. (20 )) А9 Чтобы сделать диаметры перпендикулярными друг другу, нужно: / я * м * =-1.(21) Совместная реализация соотношений (20) и (21) возможна только в том случае, если b = * a, то есть эллипс является окружностью.
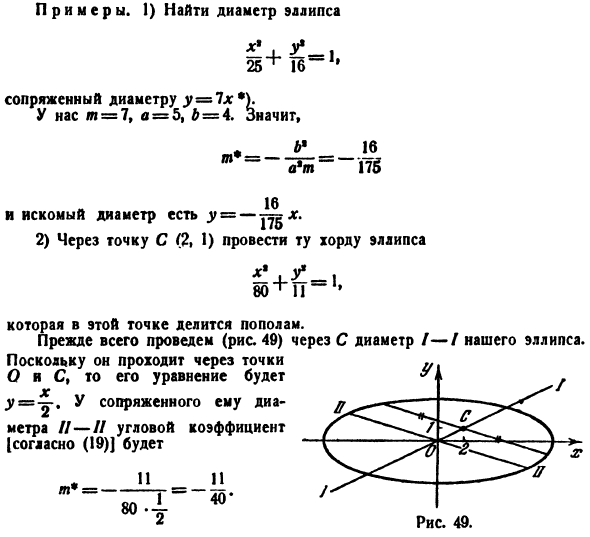
Образцы. 1) Найти диаметр eddip U 25 Чо » 1 ′ Диаметр сопряженного y = 1x•). М = 7, а = 5, 6 = 4.Три Чучело ж * = _ * e_J? 17 тонн И нужный диаметр должен быть Шестнадцать икс Сто семьдесят пять 2) нарисуйте этот эллипс Jord через точку C(2, 1) х * \ у * _И 80 ТТ В Рисунок 49. В этот момент она делится пополам. Сначала нарисуйте
диаметр эллипса/-/на C (рис. 49). Поскольку он проходит через точки O и C, уравнение y = y. угловой коэффициент сопряженного диаметра [(19)] равен И затем ЯГ. Х И затем Сорок * Угловые коэффициенты интересующего кода будут одинаковыми. Следовательно, уравнение Или !U + 40y-62 = 0.
Смотрите также:
| Линии и уравнения | Парабола |
| Прямая линия | Гипербола |

