Оглавление:







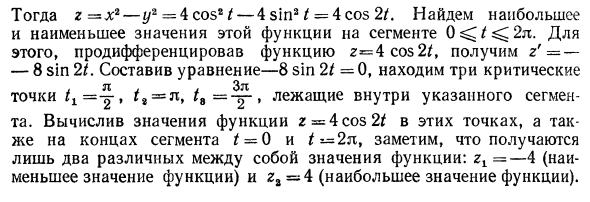
Экстремум функций двух переменных
- Предельное значение функции двух переменных Необходимые и достаточные условия существования экстремальных ценностей Понятие максимальных и минимальных значений для функций с несколькими переменными вводится так же, как и для функций с одной переменной.
Для заданной области O приведем функцию двух переменных z = f (x, y). Представлены следующие дистрибутивы: Определение Функция двух переменных z = f (x, y) = f (P), если существует окрестность этой точки, для каждой точки P (x \ y) в этой окрестности точка P0 в области G (X0 \ y0) — максимум. Неравенства кроме P0 f (Po)> f (P).
Рассматривайте эти понятия только тогда, когда они применяются к функциям двух переменных. Людмила Фирмаль
Определение Функция двух переменных zf (x, y) = f (P) имеет окрестность этой точки, и если все точки P (x \ y) в этой окрестности различны, точка PQ (x0; y0 группы G) ) Наименьшее из P0, неравенство f s «) . Точка P0, где функция z = f (P) имеет максимум (или минимум), называется точкой максимума (или минимума). Как и в случае функций с одной переменной, максимальная (или минимальная) точка не должна смешиваться с точкой, где функция принимает максимальное (или минимальное) значение в области G. Существует общее имя для максимального и минимального значений — e / ss / p-remum. Теорема (необходимый признак существования экстремальных значений). Если P0 (x0 \ y0) — крайняя точка функции z = f (x, y), Гх (* о » фу (x® »1 / о) = °
С предположением, что эти частные производные существуют в точке P0 (x0, y0). Доказательство. Частная производная функции z = f (x, y) по x в точке P0 (x0, y0) является производной функции одной переменной φ (x) -f (xt y0) в точке x = x0. Однако в этот момент функция φ (x) явно имеет экстремальное значение. В результате φ ′ (x0) = 0 (см. Главу VI, § 7, пункт 2). <p ‘(* •) = ((* o.y0), поэтому f; (x0, // o) = 0. Аналогично, вы можете указать f’y (xot y0) -0. Теорема доказана.
| Дифференцирование сложных и неявных функций | Тройной интеграл |
| Скалярное поле | Числовые ряды |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Таким образом, исчезновение частной производной первого порядка функции z = f (xy y) (если есть) в точке P0 является необходимым условием существования экстремального значения этой функции в точке P0. Функция также может иметь экстремальные значения в точках, где хотя бы одна из частных производных не существует. Например, функция z =] Лса-f-if явно имеет минимум в точке 0 (0, 0), но не имеет частной производной в этой точке. Точка, в которой первые частные производные f’x (x, y) и f’y (x, y) функции z = (x, y) исчезают или не существуют, называется критической точкой этой функции.
Однако есть важные моменты, которые не являются крайними. Например, функция z = f (x, y) =. Подумай о Xy. Первая частная производная этой функции Этот момент важен, потому что он исчезает в точке Po (0 \ 0). Однако функция r-xy не имеет экстремального значения. Фактически z (P0) = 0, но в любой окрестности точки Yao (0; 0) имеются как положительные (точки, принадлежащие I и III четвертям), так и отрицательные (точки, принадлежащие II и IV четвертям) функция
Из вышесказанного, крайние точки функции включены в важные моменты. Людмила Фирмаль
Рассмотренный пример показывает, что необходимых признаков существования экстремальных значений недостаточно. Достаточное условие существования экстремального значения в критической точке P0 (* 0> Yo) заключается в следующем. A (P0) = (P0) • (P0) — \ f «xy (P0)] *> 0, к.т. Кроме того, если fx * (P0) <0, P0 является максимальной точкой, а если Tx * (Po)> 0, существует минимальная точка. состояние A (Rao) = (Po) ‘U (po) — [fxy (P0) Y <0 Достаточно, если в критической точке P0 нет экстремального значения. Если случай A (P0) = 0, точка P0 может быть, а может и не быть крайней точкой (подозрительный случай).
В этом случае требуется дополнительное расследование. Нет никаких доказательств того, что существует достаточно доказательств, чтобы показать наличие или отсутствие крайних значений, сформулированных здесь. Пример. Найти функцию экстремума / (X, y) = + 3xu2-30x-18y. Решения. Найдите первую частную производную:
f’Ax, * /) = 3.x2 + 3 // 2-30, /; (*, r /) = bx // — 18. Если эти производные равны нулю, они получаются после базового преобразования. х * + у * = 10,2 ху Сложение и вычитание уравнения (63) для каждого члена дает: } (63) ‘2 = 4, я x * -2hu + y>
или ху = ± 2. } Решение этой системы уравнений (эквивалентно этому) находит четыре важных момента. I, (3; 1), RA 1; 3), R 3 (-1; -3) и R 4 (-3, -1). Тогда найдите вторую частную производную = fxy = 6g /; fy * = 6 * И сделать формулу A (I) = (I) /;> (I) — [/;, (I)] ‘= 36 (*> — 0, / d: * (H1)> 0, H | — минимальная точка. 2) Д (Я) <0, точка Я не имеет экстремального значения. 3) A (H3) <0, точка H3 не имеет экстремального значения. 4) D (R4)> 0, f’x (P4) <0, R4 — максимальная точка. Следовательно, эта функция имеет два крайних значения. H-Min / (H1) = -72, PA-Max / (H4) = «72. 2. Максимальные и минимальные значения функций двух переменных
Сделайте функцию z-f (x, y) непрерывной в ограниченной замкнутой области G и сделайте ее дифференцируемой в этой области. Затем он имеет минимальное и максимальное значение в этом регионе (см. § 2, пункт 5) и достигается в пределах региона или на границе. Если функция принимает максимальное или минимальное значение во внутренних точках G, эти точки явно являются крайними точками функции r = [(x, y).
Следовательно, точка, в которой функция имеет максимальное или минимальное значение, является крайней точкой функции или граничной точкой G. Достигните следующего правила для нахождения максимальных и минимальных значений функции двух переменных. Чтобы найти максимальное и минимальное значения функции z = f (x, y) в ограниченной замкнутой области G, необходимо найти значение функции в критической точке этой области, а также максимальное и минимальное значения на границе G Есть. Максимум всех этих значений является максимальным значением функции f (x, y) области G.
Минимальное значение того же значения функции является минимальным значением области G. В некоторых случаях при нахождении максимальных и минимальных значений функции двух ограниченных замкнутых переменных Удобно разделить границы этой области на части. Каждая часть определяется своим собственным уравнением. Пример. Функция r * = x2 — найти максимальный и минимальный y2 круга Решения. Найти первую частную производную zx — 2x и z’y = —2 года.
Решить одновременные уравнения 2x = 0, -2x-0, Получите одну критическую точку H0 (0; 0), где значение функции равно нулю. Найти максимальное и минимальное значения функции на границе, т.е. окружность x2 -) — | / 2 = 4. Поскольку переменные x и y связаны соотношением x2 — * — yy-Ay на окружности, если точка окружности может быть выражена как функция функции r = xg-1, переменная x: z = x * — (4-x2), то есть z = 2xg-4 и 2 ^ x: ^ 2. Так что найдите максимальное и минимальное значения двух функций: переменная на окружности x2 + y * = 4 и одна переменная z на отрезке [-2,2] z = * Максимальное и минимальное значения функции 2×2-4 Будет найден
Найдите критические точки функции в интервале (-2, 2) и вычислите значение функции в этих точках и в конце интервала (см. Главу 6, § 7, стр. 4): r ‘= 4x, 4jc = 0. Точка x = 0; z | A. = 0 = -4; zlx = -2-z | x = r = 4. Следовательно, максимальное значение функции равно 4, а минимальное значение равно –4. Следовательно, функция z = x2 — y2 диска x * + y * ^ 4 принимает максимальное значение в точках Mx (−2; 0) и M2 (2; 0) окружности x1 + y2 ^ 4 и в точке M3 Возьмите минимальное значение. UI4 (0; -2) в том же круге, что и (0; 2). Максимальные и минимальные значения функции x2 + yr = 4 можно найти по-разному. Представляет уравнение окружности в параметрической форме: l: = 2cosy-2s \ nt (0 <* <2l).
Далее r = * 2 — год-4cos * / -4sin2 / = 4cos 2 /. Найдите максимальное и минимальное значения этой функции на сегменте. Дифференцируя функцию 2 = 4 cos 2 /, получаем r ‘= -8 sin 21. Создание уравнения — 8 грех 2 / = 0 находит 3 критических , L ,. зло Точка ^ = в пределах указанного сегмента Там. Обратите внимание, что после вычисления значения функции z = 4cos2 * в конце этих точек и сегментов / = 0 и t2 получаются только два разных значения функции: zt = -4 (функции Мин) и gi = 4 (макс.) Функция).

