Оглавление:






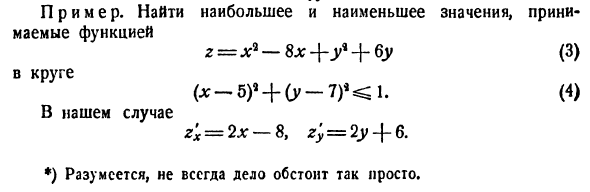





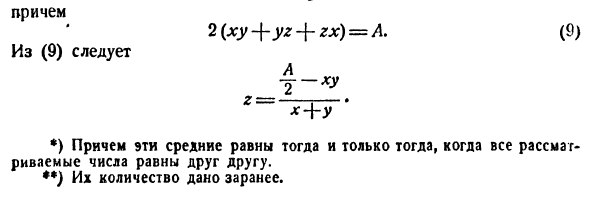



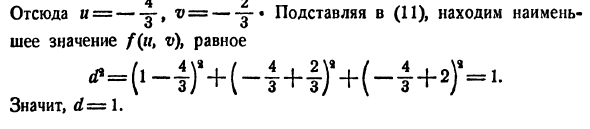

Экстремальные значения функции нескольких переменных
- Экстремальные значения функций некоторых переменных А ° 1. Определение экстремальных значений. Условия, необходимые для экстремальных значений. Для функции с одним аргументом мы дали два определения максимального значения: 1) Функция f (x) дает максимальное значение, если x0 находится точно в заданном интервале f (x) И если вы передадите x (слева направо) в jc0, функция увеличится и на 2).
Если в интервале определения функции есть интервал [p, q], функция f (x) имеет максимальное значение в некоторой точке и содержит ровно x0 внутри нее, p <^ xQ <^ q и все Вы можете видеть, что значение f (x) на (p, q \ t равно max /(.** „). Функция определения f (xt y) имеет максимальное значение в точке y0)> если существует прямоугольник Если есть только одна стационарная точка (**, yy), это / (n: *, pr), что является желаемым максимальным значением *).
Это второе определение max является переменной, мы принимаем его за два аргумента вы сформулировали. Людмила Фирмаль
Поэтому нет необходимости применять теорему № 2 (не доказано!) В рассматриваемом случае. № 4. Примеры конкретных свойств. 1) Разложите это число в термины ^ ^ 0, yО0, z O O P = XYZ Оказалось, самый большой. z = A-x — y, так > R’u = А-х * P = xy (A-x-y \ Мы решили найти максимальное значение этой функции для двух переменных при условиях x ^ 0, y ^ 0, A. Эти три Неравенство определяет треугольник S (касс. 324), необходимый для поиска Янайбе. На контуре этого треугольника есть P = 0, а внутри него P 0.
Это означает, что он находится в состоянии, описанном в начале последнего утверждения № 3. P = Axu-x * y-xy \ затем 2 ху Px = Lu-2hu-y \ И система (2) y (A-2x-y) = 0, jc (A-JC-2 ^) = 0 / 7 \ * о (7) Рисунок 324. Меня интересует решение (x, y) этой системы строго в S. В этих случаях х есть ф. 0, уф0 и система (7) упрощены. 2x + y = A, x + 2y = A Отсюда х = ~ у = б-это точка **) и максимальное значение Значение Р. Если x и y найдены, z = A-x — y = A. = 3 ”доказано Теорема.
- Произведение трех неотрицательных чисел с заданной суммой является максимальным, только если все эти числа равны. *) На самом деле, это значение неизбежно присутствует и может быть достигнуто только внутри S, но нигде (кроме четко известных). * •) Вы также можете сослаться на конец приведенного выше утверждения, поскольку оно оказывается единственной стационарной точкой внутри S.
Аналогичная теорема справедлива для произведения многих факторов. Поскольку я заметил это, получим любое n чисел Jtj> 0, …, xn> 0 и A = Xi ~ \ -x * + … + • * / • A A A Числа -, -, ….- одинаковые суммы. И все эти числа являются n 1 n ‘n J J J Если они равны друг другу, их произведение не меньше чем х: 1. Другими словами … ч- Это (8) Таким образом, некоторые положительные геометрические средние не больше среднего арифметического *). 2) Следующая задача может быть решена неравенством (8). Разложить данное число O на n положительных факторов, Сумма была минимальной.
На самом деле, если P = xxdd * … xn — разложение P, (8) + …- \ -xn ^ nV ~ P Таким образом, вы не можете получить общее количество меньше, чем n \ fP> Поэтому это было доказано Мы обнаружили, что сумма некоторых **) положительных чисел с конкретным для теоремы произведением минимальна, только если все эти числа равны друг другу. 3) Найти все кубоиды с заданной полной поверхностью A с наибольшим объемом V.
Получить сумму легко, взяв все факторы равные yfР. Людмила Фирмаль
Когда длина стороны параллелепипеда выражается через x, y, z, она становится следующей. V = XYZ, далее 2 (xy + yz + zx) = A (9) Продолжить с (9) 2_ ~ 2 Z = -: — • х + у *) Кроме того, эти средние равны только в том случае, если все рассматриваемые числа равны друг другу. **) Номер указан заранее.
смысл 2 (д: + у) Если переменные x и y положительные и 2hu A, вам нужно найти UNaib>. В других слонах точка (x \ y) должна находиться в области S, ограниченной осями координат, и гипербола 2hu = A (рисунок 325). Продолжить с (10) v, _ (Au-4dY) (x + y) — (Ahu-2d-y) l-2 (x + yy • Уравнение V’x = V’y = 0 имеет вид 2l; 5 + Axu = A, 4hu + 2y * = A. Таким образом, 2x * = 2y \, т.е. x = y. так 6x * = A «-VF- (U)
Откуда Как хорошо Рисунок 325 Тогда y = j / ^ и (9) возвращает z = y но То есть желательно Куб * это коробка. № б. Расстояние между двумя линиями в пространстве. Вышеуказанная теория позволяет легко найти расстояние d между двумя прямыми в пространстве.
Фактически эти линии могут быть определены параметрическими уравнениями x = xi + lxv, (1) y = x = xi — \ — грипп,z = Z \ + tl \ U, Z = Zi + W- Точка I, точка M, соответствующая значению параметра, и точка N, соответствующая значению линии II *) Тот факт, что значение функции V не является точно наибольшим и наименьшим в найденной точке, видно из того факта, что точка (g, y) становится V 0 при приближении к любой точке на границе области S вы можете. Это становится понятным, когда (10) переписывается в виде V = 0> (A-2xu).
Найти метр v, расстояние MN. В зависимости от и и, минимум этой функции от и и v равен требуемому расстоянию d. Пример *). Найти расстояние между линиями x + yz-1 = 0, n x — \ — 2y-z-2 = 0, m 2x-j-jf-z-2 = 0, K} x + 2y + 2z — \ — 4 = 0. {1 ) Сначала посмотрите на стандартные линейные назначения. Вычитание первого выражения из второго выражения (I) дает x = . Подставляя это значение x в одну из формул (I), получаем r. Таким образом, линия I проходит через точки (1, 0, 0) и (1, 1, 1). Ненормальные уравнения x— я y ^ r_ o ~ 1-1 •
Если сумма этих дробей обозначена как и, отсюда берется параметрическая. x = 1, y = u, z = u. Вычитание одного уравнения (II) из другого уравнения (II) дает z = –2. Подстановка этого z в одно из уравнений (II) дает je-j-2y = 0 или x-2y. Если мы возьмем y = 0 и y = 1, мы найдем две точки (0, 0, -2) и (-2, 1, -2) на линии II. Следовательно, форма канонического уравнения в строке 11 имеет вид X _y__2 + 2 -2 до 1-го И параметрический x = -2v, y = v, z = -2.
Таким образом, M (1, u, u) — это точка на линии I, а A / (-2 v, v, -2) — это точка на линии II. Квадрат расстояния MN равен f (u, r0 = (1 + 2t>) * + (a-x>) * + (i / + 2) * (U) Различает f (u, r>) по u и v и выравнивает f’a и f ‘. 2n-r> — {- 2 = 0, 5z> -n + 2 = 0.Следовательно, если подставить u = -y и v = — (11), минимальное значение f (ti, v) равно ‘- (‘ — 4r + H + iM-l + ‘H. Следовательно, d = 1.
В области определения функции, включая y) строго внутри себя и принимая f (x, y) с p Xq y0), то есть функция / (x> Y * 1 для x = x0.). То есть / (x, yy) является максимумом в этой точке. х = х0. Следовательно, производная функции f (x, jy0), где x = x0, равна 0. Но эта производная есть только частная производная fx (q «o, yj) -so fx {* o» .Uv) = 0 * Ситуация аналогична fy (x0, y0). Следовательно, координаты (x0, y0) точны. P b 9 Рисунок 322. 0) fx (xo, yo) = 0, fy (x * yo) = a
Ясно, что для минимального балла соотношение (I) также должно быть выполнено. Обратите внимание, что все точки (независимо от того, существуют ли крайние точки), где выполняется соотношение (I), называются стационарными точками. Поэтому крайние точки Всегда стационарно. Одновременные уравнения GLx> y) = 0, Gu (x, y) = 0 Содержит два уравнения и два неизвестных. Таким образом, вообще говоря, эта система может быть решена путем нахождения одного или нескольких остановок. № 2 дает правила для ясности
Проблема в том, имеет ли заданная точка покоя (x0, y0) экстремальное значение, если так, но сейчас, например, для функции трех переменных f (xt y, r): Нахождение крайних точек решит три системы: Уравнение с тремя неизвестными: f; (, y, z) = 0, fy (x, y, z) = 0, f; (, y, z) = 0. Это означает, что число уравнений здесь соответствует числу неизвестных. № 2. Правила изучения стационарных точек. Предположим, что исследуемая функция f (xt y) имеет непрерывные частные производные первого и второго порядка *) fxt f ^ fXXt fxy> f’x, f%. Пусть (xv _y0) точка покоя строго в области функций. Put fxx (x 0, крайнее значение равно * (♦), которое является максимальным, если A <0, и минимальным, если A> 0 ***).
Я не доказываю эту теорему. Обратите внимание, что случай A = 0 ♦♦ **) не охватывается. Однако эта теорема часто решает проблему природы точек (xv y0). Пример. 1) z = x * — \ — y * —9hu. Где z’x = 3xa-9y, z’v = 3y * — 9x. Поэтому, чтобы найти стационарную точку, необходимо решить уравнения одновременности jt9 = 3y, y% = 3x. Первое уравнение у = гх *. Подставляя это во второе, получаем x4-27 * = 0. x имеет два значения: Jtj = 0 и qr ^ = 3. Таким образом, найдены две точки покоя (0, 0) и (3, 3). zxx = 6x, zxy = –9, Zyy = 6yt, поэтому в точке (0, 0) A = 0, £ = -9, C = 0, тогда D = AC- £ a = -81 <0 полюс Там нет значения балла.
Точка (3, 3) имеет A = 18, B = -9, C = 18, т.е. A = 324-81 *> 0, и имеет экстремальное значение. с того времени Если i4 ^> 0, это минимальное значение. •) Напомним / Iv = / Jx. * •) Обратите внимание, что для одной переменной с точкой покоя x0 существует максимальное значение f (x0) <0 и минимальное значение f (x0)> 0. ** ♦) Если >> 0, AC> Br, особенно AC> 0.
Поэтому (если >> 0) числа A и C имеют одинаковый знак, поэтому можно говорить о С вместо теоремы. , ****) Как и в случае с одной переменной, оказалось, что второй метод проверки точки покоя x0 неприменим к f (d0) = 0. 2) z = * 4-f- /. Где z’x = 4jc3, z; = 4 /, z; v = 0, 12% Точка покоя (0, 0). Среди них A = B = C = 0 и, следовательно, A = 0. Другими словами, теорема не применима. Однако в точке (0,0) r = 0 и во всех других точках z> 0, поэтому вы сразу видите, что здесь есть минимум *). № 3. Найти максимальное и минимальное значения функции.
Предположим, что функция f (x, y) задана и непрерывна в области S, окруженной замкнутым контуром K (рис. 323). Возникает проблема нахождения максимального значения этой функции. Когда это значение достигается в точке (jcq, y0) строго в области, функция f (x, y) явно максимизируется в этой точке. Однако наибольшего значения для нас можно достичь даже с точками на контуре К. Поэтому вам нужно найти все точки, чтобы решить проблему. O «ZG максимум, рассчитать лежащий внутри Рисунок 323. Значения функций и сравнение с этими значениями Максимальное значение, принятое функцией контура K — используя аналитическое определение контура K, можно найти это последнее значение.
Например, эта схема задается параметрическим уравнением * =? (0, у =) (т) (р ^ т ^ д). Тогда любая точка (x, y) контура определяется путем установки некоторого значения (в этой точке f (x> y) = f [<* (*)> + С01- Другими словами, в контуре K функция f (xt y) становится функцией F (t) с одним аргументом /, и можно определить вопрос, то есть интервал [p, q \ t. Конечно, все, что сказано, переносится, когда необходимо найти минимальное значение функции.
Пример. Найти максимальные и минимальные значения, которые принимает функция 2 = x * -8x — \ — y * + 6y (3) По кругу 5) 1 + (y-7) << 1. (4) В нашем случае z’x = 2x-8, Zy = 2y — \ — 6. *) Конечно, это не всегда просто.Система с уравнениями zx = 0 и z’y = 0 дает единственную точку покоя (4, -3). Точка эго находится вне круга (4), поэтому внутри точечного круга нет экстремумов.
Поэтому интересующее нас значение достигается в окружности, которая окружает круг (4). Параметрическое уравнение этого круга X-b cos /, y = 7 + sin / (0 </ <2m :). Подстановка этих выражений x и y в (3) приводит к: z = (5 + cos 0e -8 (6 + soo0 + (7 + sin /) * +6 (7 + sin /), Это * = 77 + 2 cos / + 20 sin /. (5) Необходимо найти максимальное и минимальное значения функции (5) в интервале [0, 2te]. Дифференцировать, найти = 20 cos / –2 грех /. Установка z \ = 0 означает грех / = 10 cos / тг / = 10 (6) Если 0 <; / <^ 2, существует только один угол δ, который удовлетворяет (6) *).
Следовательно, tg9 0 = 100, sec10 = 101, cos0 = TL -_, sin 0 1 (1 / Гот гм * [Другие углы 0, 2tcJ удовлетворяют (6), поэтому 5 = 0 + tm. Для него р б ю а 1 sin 0 = -rm =, cos 0 — r =. / 101/101 Соответствующее значение z * (8) == 77 + — ^, z (0) = 77— V ‘1/101 V’ / 101 с того времени z (0) = * (2 *) = 79, * Вы z (0) и z (9) — максимальные и минимальные значения r. Замечания. На самом деле, если вы знаете, что каждое место в K имеет f (x, y) = 0 и / (* внутри S, задайте его в области S, ограниченной замкнутым контуром K Функция f (x, yX y)> 0.
В этом случае найдите все максимальные точки функции в S и просто выберите точку в S, которая дает максимальное значение функции (при определенных условиях) Очевидно, этого достаточно. *) Можно найти 0 = 84е17 ’22 \ из таблицы
Смотрите также:
| Преобразование координат | Полный дифференциал |
| Производные функции нескольких переменных | Понятие о системах дифференциальных уравнений |

