Оглавление:



Экспериментальное изучение работы материала при чистом изгибе
- Экспериментальное исследование работы материала при чистом изгибе. После изучения диаграмм изгибающего момента и поперечной силы можно вернуться к задаче расчета нормальных и касательных напряжений в выбранном сечении. В результате было доказано, что нормальное напряжение зависит только от изгибающего момента.: Е=/I (а-л). Т(<?)• (12.1) (12.2) Фигура. 180 это
позволяет упростить расчет о в особых случаях изгиба балки при q=0. Полученное выражение допустимо и в других случаях. Изгиб балок с нулевым боковым усилием вполне возможен, если пренебречь собственным весом балок. Для этого необходимо, чтобы система внешних сил, приложенных к отрезанной части балки,
приводила всего лишь к паре сил. Примером может служить изгиб осей Людмила Фирмаль
железнодорожных вагонов (см.§ 69). Схема действия силы показана на рисунке. Возьмите участок между 180 точками C и D, и для любого из этих участков изгибающий момент и боковые силы равны каждому M (x)-P x-P(x-a)=RA = const, Q (x)=P-p=0. Таким образом, во всех сечениях центральной части оси CD изгибающий момент постоянен, а боковая сила равна нулю (Q=чистый изгиб для такого изгиба). Отрежьте этот луч(рис. 180, а) отрезок расстояния х от левого края. Отрезная часть (рис. 180, б) изгибающий момент действует только М-Р А и нормальное напряжение. Равновесное состояние отрезной части требует, чтобы эти напряжения были приведены попарно на рабочую поверхность внешней силой—плоскостью симметрии балки. Однако
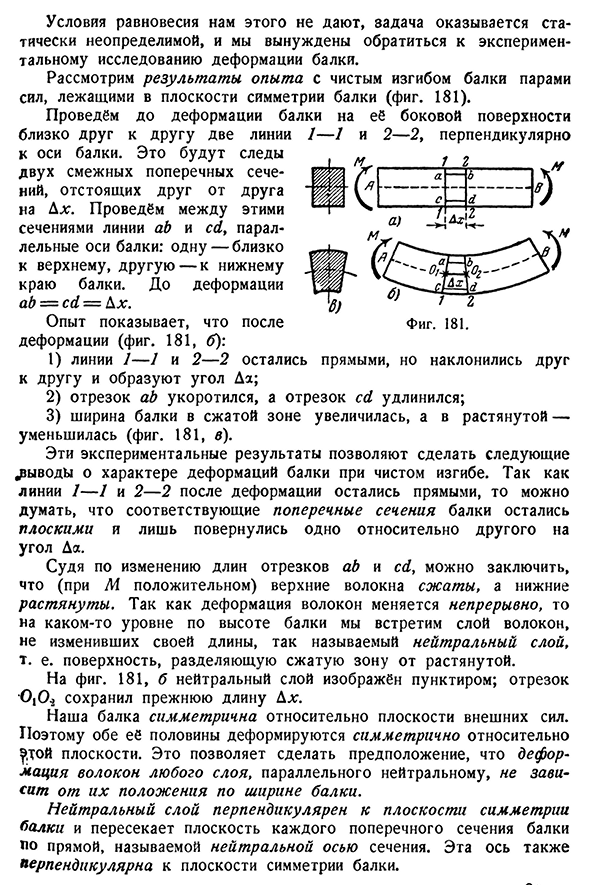
для того, чтобы найти наиболее напряженную часть материала, можно рассчитать напряжения в каждой точке сечения и знать распределение напряжений во всем сечении§ 77]исследование работы материала в изгибе 25.& И 2 к 2, перпендикулярно к Фигура. 181. decreasea — ’ gg S*и S ATIME 111к С Д Условия равновесия не дают нам этого, задача оказывается статически неопределенной, и мы вынуждены обратиться к экспериментальному исследованию деформации балки. Рассмотрим результаты эксперимента с сетчатым изгибом балки парой сил на плоскости симметрии балки(рис. 181). Прежде чем балка деформируется,
- нарисуем две линии на оси балки рядом с ее стороной. Между участками линий ab и cd проведите их параллельно оси балки: один ближе к верхнему, а другой-к нижнему краю балки. Перед деформацией ab=cd — &X. Опыт показывает, что после деформации(рис. 181, Б): 1) линии 7-7 и 2-2 друг с другом и образующие угол да;2)укорочение отрезка АВ, а отрезок cd удлиняется;3) увеличение ширины пучка в зоне сжатия, 181, в). Из этих экспериментальных результатов получены следующие выводы о характере деформации балки при чистом изгибе. Линии 7-7 и 2-2 остаются прямыми после деформации, поэтому можно считать, что соответствующее поперечное сечение балки остается Прямо,
но криво. Превратили одно относительно другого в плоский и только да укромный уголок. Судя по изменению длины сегментов ab и cd, можно сделать вывод, что (при М-положительном) верхние волокна сжимаются, а нижние растягиваются. Поскольку деформация волокон изменяется непрерывно, на определенном уровне по высоте пучка образуется слой волокон, не изменившихся по длине, так называемый нейтральный слой, то есть зона сжатия. Как использовать 181, B нейтральный слой представлен
пунктирной линией; сегмент 010.2 сохраняет ту же длину DX. Наш луч Людмила Фирмаль
симметричен относительно плоскости внешней силы. Таким образом, обе половины деформируются симметрично для^.Это позволяет сделать предположение, что деформация волокон любого слоя, параллельного нейтральному слою, не зависит от их положения по ширине пучка. Нейтральный слой перпендикулярен плоскости симметрии балки и пересекает плоскость каждого сечения прямой балки, называемую осью нейтрального сечения. Эта ось также перпендикулярна плоскости симметрии луча. 9e260 расчет нормального напряжения изгиба [глава XIII Поворот секции происходит вокруг ее нейтральной оси, как показано на рисунке. 181 балл Oj и O2. Если вращение сечения не происходило вблизи оси,
находящейся в нейтральном слое, то отрезок не мог удерживать свою первоначальную длину. Так как сечение вращается вокруг нейтральной оси, перпендикулярной рабочей поверхности силы, то точка этой плоскости остается в ней после деформации, поэтому ось балки остается на рабочей поверхности силы и уплощается. Изгиб, при котором ось балки после деформации остается на рабочей поверхности под действием внешней силы, называется плоским изгибом. Наконец, деформация материала балки в направлении ее ширины, при которой ее волокна испытывают нормальное растяжение или сжатие, есть явление, рассматриваемое
коэффициентом Пуассона 181, в). Экспериментальные исследования изгиба балки дают основание для многих предположений, которые служат основой для дальнейших выводов: 1. При чистом изгибе поперечное сечение, которое было плоским до деформации, остается плоским во время деформации (так называемая гипотеза плоского поперечного сечения). 2. Поскольку продольные волокна не прижимаются друг к другу, они испытывают простое линейное растяжение или сжатие под действием нормального напряжения. 3. Деформация волокон не зависит от их расположения по ширине поперечного сечения. В результате нормальное давление,
изменяющееся по высоте секции, остается неизменным по ширине. В дополнение к этим предположениям мы вводим еще одно ограничение 1. Луч имеет по крайней мере одну плоскость симметрии, и все внешние силы находятся в ее плоскости. 2. Материал балки следует закону крюка, а модуль упругости при растяжении и сжатии одинаков. 3. Соотношение между размерами балки таково, что она работает на плоском изгибе без деформации и скручивания. Эмпирически известно, что балка с малой шириной поперечного сечения подвержена потере устойчивости плоской формы при изгибе (скручивании). При соотношении высоты прямоугольного поперечного сечения балки к ее пролету
y o n a работает не как балка, а как плита, и условия ее расчета изменятся. Приведенное выше предположение в нормальном случае изгиба является почти единственно правильным. Но ошибки, возникающие в результате теории, ничтожно малы (за исключением особых случаев).
Смотрите также:

