Оглавление:



Экспериментальная проверка теорий пластичности
- Экспериментальная проверка теории пластичности. Начиная с 1928 года, когда были опубликованы фундаментальные исследования по верификации экспериментальной теории пластичности Родса, этому вопросу был посвящен ряд работ. В настоящее время подобные исследования проводятся в нашей стране и за рубежом, но центральной проблемой в настоящее
время является поиск закономерности пластической деформации при несбалансированных нагрузках. Универсальной теории пластичности, дающей достаточно надежный результат при любой нагрузке, пока не существует, но вопрос накопления экспериментальных материалов и фазы проверки различных гипотез проблему закона пластичности при
пропорциональной нагрузке стали теперь можно считать решенной. Людмила Фирмаль
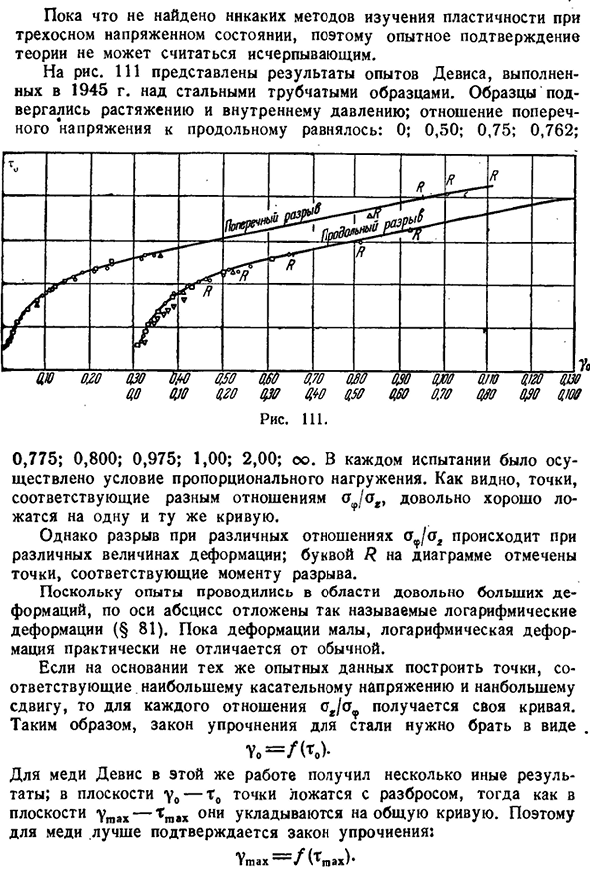
Единственным надежным способом создания однородного состояния давления в образце является испытание тонкостенных трубок на совместное действие осевого натяжения, внутреннего давления и кручения. Указывает средний радиус трубы через R, толщину стенки через b, растягивающее усилие P, внутреннее давление q и крутящий момент M. определите напряжение, возникающее в результате 1. Является ли поперечное сечение трубки
приблизительно равным 2l/?B. направление оси z вдоль шины,°*=2nRS ’ (80.1)§ 80] экспериментальная проверка теории пластичности 171 все силы на оси Y. 2. Внутреннее давление вытягивает трубку в поперечном направлении, возникает растягивающее напряжение в продольном сечении трубки, которое указывает на Ст^. Для определения этих напряжений используйте
- фиг. 110, показывающая половину диаметра плоскости рассеченной трубки. Если длина трубы равна I, то площадь трубы уменьшается на растягивающее напряжение (o, f), параллельное оси Y. Основная полоса IRdtp, назначенная вдоль шины-линии угловой координаты®=2Г^(з -°). 8. е~2Г^^а т е г
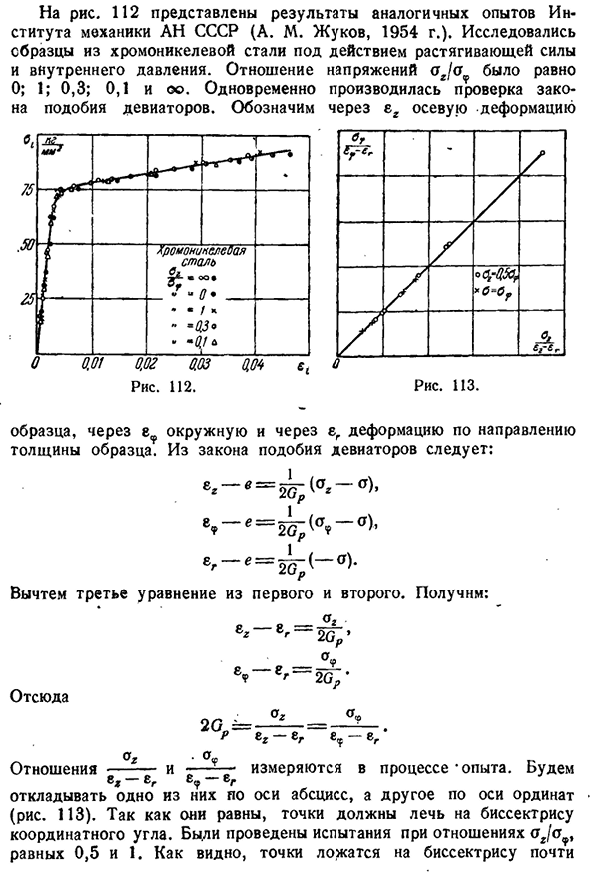
е ~ е ~ 2 6^Вычтем третье уравнение из первого и второго. Возьми: е з-поэтому 8R-2^> в < P > С ’ ~~2Г/>’ И так оно и есть. 2Г===■ -=. Р®з — ®г®<р — ®г — 1 опыт измерения в процессе. Один находится на оси абсцисс, другой-на оси ординат г Отношение — — — — — — — — —
и отложить любое из 8G — £g(рис. И З). Поскольку они равны, точка должна находиться на биссектрисе координатного угла. Испытание проводили в соотношении 0,5 и 1. Как видно, точка находится на биссектрисе теории пластичности и нелинейной упругости[ГЛ. ВИ Если быть точным, то разница не выходит за рамки обычного случайного разброса. В случае некоторых алюминиевых и магниевых сплавов закон упрочнения не соблюдается как в одной форме, так и в другой(С. И. Ратнер). Что касается условий пластичности, то основная экспериментальная трудность заключается в том, что момент достижения пластического
состояния весьма условен и может быть определен различными способами. Людмила Фирмаль
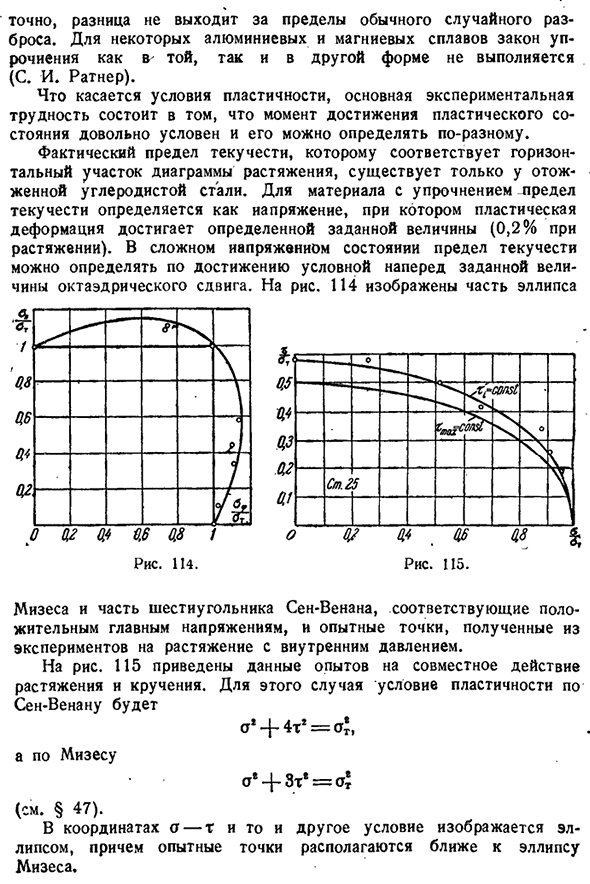
Фактический предел текучести, соответствующий горизонтальному сечению диаграммы растяжения существует только в отожженной углеродистой стали. Предел текучести упрочненного материала определяется как напряжение, при котором пластическая деформация достигает заданного значения (0,2% в момент натяжения). В сложных напряженных условиях предел текучести может быть определен путем достижения условно заданного значения сдвига октаэдра.
Для риса. 114 показывает часть эллипса Часть шестиугольника Сан-бенанта, соответствующая положительному главному напряжению, и экспериментальная точка, полученная из эксперимента по внутреннему напряжению давления. Для риса. Приведены данные эксперимента по совместному действию растяжения и кручения. В этом случае пластичность Сен-Венана выглядит так о * — ф-выводам 4t2=£, Фон Мизес а * ЗТ ’ =<4 (См.§ 47). В координатах a-t оба условия представлены эллипсами, а тестовая точка расположена вблизи эллипса Мизеса.
Смотрите также:
| Закон упрочнения | Конечная деформация |
| Деформационная теория пластичности | Нелинейно упругое тело |

