Оглавление:





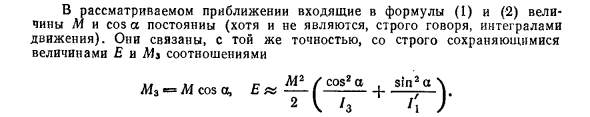

Эйлеровы углы в физике
- Угол Эйлера. Как уже указывалось, для описания движения твердого тела Используя три координаты его центра инерции Три угла, которые определяют направление осей x1, x2j x% движущейся системы координат относительно неподвижной системы X, Y, Z. Угол Эйлера. Меня сейчас интересует только угол оси В ординате выберите начальную точку для обеих систем в одной точке (Рисунок 47).
Движущаяся плоскость x \ x2 пересекает статический XY прямой линией (ON на рис. 47). Это называется линией узлов. Эта линия явно вертикальная Рисунок 47 является линейным для осей Z и ZH. Векторное произведение [ГГц] (где z и x3 — единичные векторы в направлении осей Z и zh.
определяемом законом винта вокруг осей Людмила Фирмаль
В качестве величины определить положение осей хх, х2, ж Для осей X, Y, Z возьмем следующие углы: угол 0 между осями Z и zh, угол φ между осями X и N, угол между осями n ) ми N и XI. Углы φ и ^ отсчитываются в направлении, Z и Ж3 соответственно.
Угол 0 Пропускает значения от нуля до tg и от угла рис. 1) до 0 до 2 n г). Здесь составляющая вектора угловой скорости ft равна Подвижные оси xx, x2, zs и их производные по углам Эйлера. Для этого спроецируйте угловые скорости на эти оси 0, φ, η). Угловая скорость 0 направлена вдоль линии узла, Его составляющие по осям xx, x2, zx равны: 01 = 0 стоимость];, 02 = -0 sinij;, 0з = 0.
- Угловая скорость φ направлена вдоль оси Z. Ее проекция Ось x3 равна φz = φcos0, а проекция на плоскость † 1 † 2 равна φsin0. Разбирая последние на компоненты по осям Ж1 и Ж2, Мы получаем F1 = φsin0 simp, Ф2 = фsin0 cosip. Наконец, угловая скорость n1) направлена вдоль оси Ж3.
Сбор всех этих компонентов вдоль каждой оси выглядит следующим образом В конце: fix = φsin0 sinij; + Gcosij;, ^ 2 = Фsin0 cosij; -0 sini |;, (35,1) T2z = φcos0 + \ При выборе осей Ж1, Ж2, х% вдоль главной оси инерции Вращательная кинетическая энергия выражается в углах Эйлера, полученных путем подстановки (10) для тела, а затем (32.8). 1 \ = 12 симметричный верхний регистр Дем после простого приведения: TBp = — ^ (φ2sin2 0 + 02) + — ^ — (φcos 0 + ^ ф) 2. (35,2)
что эту формулу легче получить, используя производительность для выбора основного направления Людмила Фирмаль
Обратите внимание, что эту формулу легче получить, используя производительность для выбора основного направления. Оси инерции xx, x2 на оси симметрии. Ось x \ соответствует оси ON узла. Если η> 0, получается более простое выражение угловой составляющей скорости fix = 0, P2 = φcos0, Г2з = φcos 0 + \ j>. (35,3)
В качестве простого примера использования углов Эйлера С их помощью мы определим свободное движение уже известного симметричного волчка. Выберите ось Z фиксированной системы координат направления Постоянного момента вершины М. Точка времени с осью узла.
Далее о компонентах вектора М Найти по формуле (35.3): Mi = Jxfix-Л0> М2 = / 2 ^ 2-I2Ф в 0, M3 = J3fi3 = / 3 (φcos0 + r |;). С другой стороны, ось х \ (линия узла) является вертикальной, Линейный к оси Z, Mi = 0, M2 = M sin 0, M3 = M cos 0 Выравнивание друг друга с этими уравнениями дает: 0 = 0, / xf = AG, / s (φcos 0 + ‘φ) = M cos 0. (35.4) Первое из этих уравнений 0 = const, т. Е. Угол инвариантности Верхняя ось наклона относительно направления М.
Второй Угловая скорость прецессии (согласно (33.5)) равна φ = M / 1 . Наконец, третье определяет верхнюю угловую скорость вращения вокруг своей оси = M cos 0 // 3. Задание 1. Уменьшите проблему перемещения тяжелого симметричного верха, закрепленного снизу, до квадратуры (Рисунок 48). Решения.
Начало координат движущейся системы координат и фиксированной системы координат выбирается в качестве фиксированной точки верхние оси O и Z ориентированы вертикально (Рисунок 48). Верхняя лагранжева функция гравитационного поля B = ^ ± ^ (0 2 + φ% 1n2 0) + + ^ (4> + Фото в) 2-Ixgl COS 0 (C — верхняя масса, I — расстояние от нижней точки до центра инерции). Координаты n ) и (p периодические.
Таким образом, есть два интеграла движения. Rl > = — = / sSF + φCOS 0) дл> const = M3, (1) 8L p f = q-r = (/ {sin2 0 + / 3 cos2 0) f + / z’F cos 0 = const = Mz, (2) Здесь введено обозначение 1 [= + + \ xl2 (величины pf и pf являются компонентами вращательного момента, определенного относительно точки O вдоль осей z3 и z соответственно). Кроме того, энергия сохраняется. т>. T E = — ^ (02 + φ2sin2 0) + — ^ ■ (‘Ф + Фcos 0) 2 + | xgl cos 0.
Из уравнений (1) и (2) 0 |>: f = M3 Mz-Ms cos 0 с 0 Я [sin2 0 ’ Mz-Ms cos 0 (3) (4) (5) Получить E ‘I’lnе * + ψ ()) из энергии (3) с помощью этих уравнений ψ и η (). Где введены обозначения Th 2 / s 2 I [s i n 2 0 — | X г / (1-C O S 0). (6) Определите 0 отсюда и отделите и получите переменную дд т: / (7) 0i ljr (E ‘-U, Ф (0)) (Целое число является овальным.) Углы Ф и 0 затем выражаются как функция от 0 в квадратурной форме с использованием уравнений (4) и (5).
Диапазон изменения угла 0 во время движения определяется условием E ‘^ ^ U3ph (0). Функция Ј / eff (0) (для Mz M Mz) имеет тенденцию быть + oo для значений 0 = 0 и 0 = 7Г и проходит минимальное значение на этих интервалах. Таким образом, уравнение E ‘= Ј / eff (0) имеет два корня, которые определяют граничные предельные углы 01 и 02.
Верхняя ось относительно вертикали. При изменении угла 0 С 01 по 02 Знак производной f остается неизменным, или Разница Mz-Mz зависит от того, изменяется ли знак cos0 или изменяется на этом интервале.
В первом случае верхняя ось монотонно прецессирует вокруг вертикали и одновременно Вибрация вверх-вниз (так называемая нутация) (рис. 49 а; линия показывает след, который рисует верхняя ось на поверхности сферы с центром в верхней фиксированной точке) Во втором случае направление прецессии Два ограничивающих круга перевернуты, и верхняя ось перемещается вокруг вертикальной линии, рисуя петлю (Рисунок 49b).
Наконец, 1 Когда значения 01 и 02 соответствуют нулю, соответствующая ограничительная окружность φ и разность Mz-Мзcos 0 на 0 исчезают одновременно. Следовательно, верхняя ось представляет путь, показанный на рисунке. Тип 49 2. Найти условия, при которых верхнее вращение вокруг вертикальной оси устойчиво. Решения.
Если 0 = 0, оси x3 и Z совпадают, поэтому M3 = Mz, E ‘= 0. Если значение 0 = 0, вращение вокруг этой оси стабильно. Соответствует минимальному значению функции Ј / eff (0). Для маленьких 0 «M? ЦЈГ 81 [2 При нахождении условия M |> 4 / J \ igl или 4 Ильигль «I> 3. Определите движение вершины, когда кинетическая энергия вращения больше, чем энергия гравитационного поля (так называемая «быстрая» вершина).
Решения. В первом приближении, игнорируя гравитационное поле, происходит свободная прецессия верхней оси вокруг направления момента М. (Соответствует верхней главе в этом случае); она следует (33.5) Доступная угловая скорость F ^ HVT-м A ‘(1) к Каждый период нутации к В следующем приближении появляется прецессия с медленным моментом Вертикаль М (рисунок 50).
Усредните точное уравнение движения, чтобы определить скорость этой прецессии (34,3) йМ дт Момент гравитации, действующий сверху jji [ri3g], где Pz — единичный вектор в направлении верхней оси. Учитывая симметрию, результатом усреднения K на «цилиндре» является замена вектора p3 его проекцией. cos os-M / M направление M (угол между os-M и верхней осью).
Получите уравнение т _ дм ярд ——— = -r p i GU 1 dt ‘C0SaM ^ gM]’ Это означает, что вектор M прецессирует вокруг направления g (вертикального) со средней угловой скоростью. ^ pr-] X I CWOSOS-ё (2) Рисунок 50 (маленький по сравнению с Onut). Для рассматриваемого приближения величины M и cos os в уравнениях (1) и (2) Постоянная (строго говоря, не интеграл движения). Они являются строго консервативными величинами и связаны с одинаковой точностью Отношения между E и Ms ~ Мл ~~ 2 ~ M3 = M cos os,
Смотрите также:
| Момент импульса твердого тела | Уравнения Эйлера в физике |
| Уравнения движения твердого тела | Асимметрический волчок в физике |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.

