Оглавление:




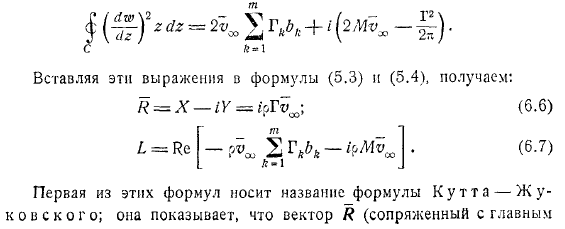


Эффективное вычисление гидродинамических реакций при установившемся течении. Формула Кутта-Жуковского
Поток, полученный введением тела в поступательный поток, предполагается потенциально расположенным в любом месте вне тела и может быть достигнут заменой тела на положение особой точки потока, гидромеханики вихря внутри контура, окружающего тело, источника и двойной линии; кроме того, существование всех источников предполагается алгебраически, что соответствует тому факту, что поток скорости через контур тела должен быть равен.
To упростив расчет, ограничимся дискретным размещением особенностей и предположим, что рассматриваемый поток определяется задачей: простых источников точки также обладает потенциалом существует формула Блазиуса-Чаплыгина циркуляция является дублетом моменты. Комплексный потенциал потока равен, а комплексная скорость. Отображается в формате. Вычисление контурного интеграла позволит найти остаток подынтегральной функции точки, так как является регулярным по всей внешней плоскости контура, содержащего точку. Вблизи последней точки комплексная скорость четко представлена разложением. Таким образом, расширение степени подынтегральной функции в ближайшие окрестности.
Теорема Жуковского — теорема о подъёмной силе тела, обтекаемого плоскопараллельным потоком идеальной жидкости или газа. Сформулирована Н.Е. Жуковским в 1904 году. Людмила Фирмаль
- Теперь в форме, и в известной теоремы об остатках:вычислить. С коэффициентами, достаточно для расширения разделов, разложение в окрестности точки бесконечности. Например выражения: тогда без труда находим: можно назвать источник и развитие дофаминовых рецепторов, окруженных в организме.Таким образом, выражения имеют вид. Если вставить эти выражения в выражения, то получится следующее выражение.
Первая формула этих формул называется Кутта Жуковского. Показано, что вектор вращается под прямым углом к вектору комплексной скорости в направлении с тем же знаком циркуляции. Если перейти к формуле применение метода конформного отображения зеркальному отражению от оси также будет перпендикулярным, только направление вращения от будет перпендикулярным. Направление вектора определяется вращением вектора v под прямым углом к направлению циркуляции, то есть знак поворота является Афиной циркуляции.
Подъёмная сила сегмента крыла бесконечного размаха равна произведению плотности газа (жидкости), скорости газа (жидкости), циркуляции скорости потока и длины выделенного отрезка крыла. Направление действия подъёмной силы получается поворотом вектора скорости набегающего потока на прямой угол против циркуляции. Людмила Фирмаль

