Оглавление:





Двузначные представления конечных точечных групп
- Две цифры Облако конечных точек Состояние системы с половинным целочисленным спином (Суммарный момент) соответствует двузначному представлению Точка в группе точечной симметрии этой системы. Это Из-за общего характера спинора, Обе группы конечных точек. В связи с этим Нужно найти двузначный непривод Представление конечного облака точек.
- Как уже упоминалось, двузначное представление по существу Для общества это не настоящее выражение группы. В частности, оно не включает обсуждаемые отношения § 94 речь и когда в этих отношениях (например, отношения (94.17) Сумма квадратов неприводимых размеров Представление) Это все невосстановимое представление, После этого только те, которые правдивы и понятны Представление.
Полезно, чтобы найти 2-значные выражения Примите следующий искусственный трюк (Н. А. Бете, 1929). Людмила Фирмаль
Раскройте концепцию нового элемента группы чисто формальным способом py (обозначается Q) -2 тг вращения Любая ось — как не единственный элемент Совпадение E в двойном приложении: Q2 = E В соответствии с этим вращение Cn вокруг оси симметрии Вторичный обеспечивает только идентичные преобразования После удвоения заявки (не n раз): Cn = Q, Cln = E (99,1).
Инверсия как любой вид коммутативного элемента I Да, даже если применять дважды в рот E. Однако двойное отражение в плоскости равно Q, Не E: cr2 = Q, a4 ‘= E (99,2) (Это отражение де а = / с 2). В результате мы получаем набор элементов Построить симметрию фиктивного облака точек rii, порядок вдвое больше, чем в исходной группе. Мы говорим об этих группах как о двойных точках Группа. 2-значное представление действительных точек Группа явно не двусмысленная.
Так как это позиция соответствующей двойной группы, Оказывается, можно применять обычные трюки. Количество двойных групповых классов больше, чем количество исходных групп ne (но обычно не удваивается). Элемент Q взаимозаменяем с Все остальные элементы группы 1) и поэтому всегда состоят Сам класс. Если ось симметрии находится на обеих сторонах, В двойной группе это сопряжение элемента Sk и C2n ~ k = QC ^ ~ k.
В этот момент при наличии второй оси Распределение элементов по классам также зависит Находятся ли эти оси с обеих сторон (в нормальных точках) Это не важно, потому что C2 соответствует обратному. Поверните C2-1). Следовательно, в группе T вторичные оси эквивалентны, Один из них двусторонний, а кубическая ось эквивалентна. Но не двусторонний. Таким образом, 24 элемента удвоены Группа Т / 2) делится на 7 классов: E, Q, 3 класса C2 и 3 C2Q, класс 4Сз, 4С |, 4C3Q, 4CfQ.
Среди всех неприводимых выражений двойных точек Выражение, соответствующее первой группе Четкое представление простой группы (и Как и E, Q соответствует единичной матрице), и Двузначное представление второй простой группы и Элемент Q соответствует отрицательной единичной матрице. Я в настоящее время интересуюсь этими последними идеями.
Двойная группа C fn (n = 1, 2, 3, 4, 6) и S4, и Простые группы, связанные с ними, являются круговыми группами м и 3). Их неприводимые представления все одномерные, Может быть найден без труда, как описано в § 95. Группа D fn (или изоморфное неприводимое представление) im C fnv) можно найти так же, как Простая группа. Эти выражения выполнены Функция вида e ± rk1p. Где ip — угол поворота вокруг n-й оси.
Порядок и k целочисленных значений приведены в пол (целочисленные значения Нормальное четкое выражение). Po Bo Компании вокруг вторичной горизонтальной оси переводят Эти функции взаимодействуют, и вращение Cn умножается на e ± 2shk / pt. Найти выражение double qu Большая группа. 24 элемента группы T f распределены по 7 х) В случае инверсии это ясно.
Для отражения на плоскости Это основано на том факте, что отражение может быть выражено как произведение Инвертировать и вращать. 2) Различают двойные группы с нормальными штрихами групповых символов ру. 3) x∈S 2 = S q = включая обратную группу x Я покинул группу, но это не периодически. Класс. Таким образом, есть только 7 неприводимых выражений 4 из них Стенд группы Т.
Сумма квадратов для оставшихся трех измерений Выражение должно быть равно 12. Они двухмерные. Поскольку элементы C2 и C2 Q находятся в одном, Класс, тогда x (Cb) -x (^ 2Q) = -x (C2) Все три выражения x i p 2) -0. Кроме того, из трех выражений По крайней мере, один должен быть подлинным. Насколько сложные выражения выполняются имно сопряженная пара.
Учитывайте это мнение Предположим, что матрица элемента C3 сокращена по диагонали Форма (ai, <1 2 — его диагональный элемент). с того времени ku s | = Q, тогда af = a \ = -1. x order (C3) = a \ + a2 Так как это было правдой, нужно взять a1 = ex / 3, az = e-7r / 3. Отсюда x (C3) = 1, x (Cf) = a i + a2 = -1 * Поэтому Найдено одно из обязательных представлений.
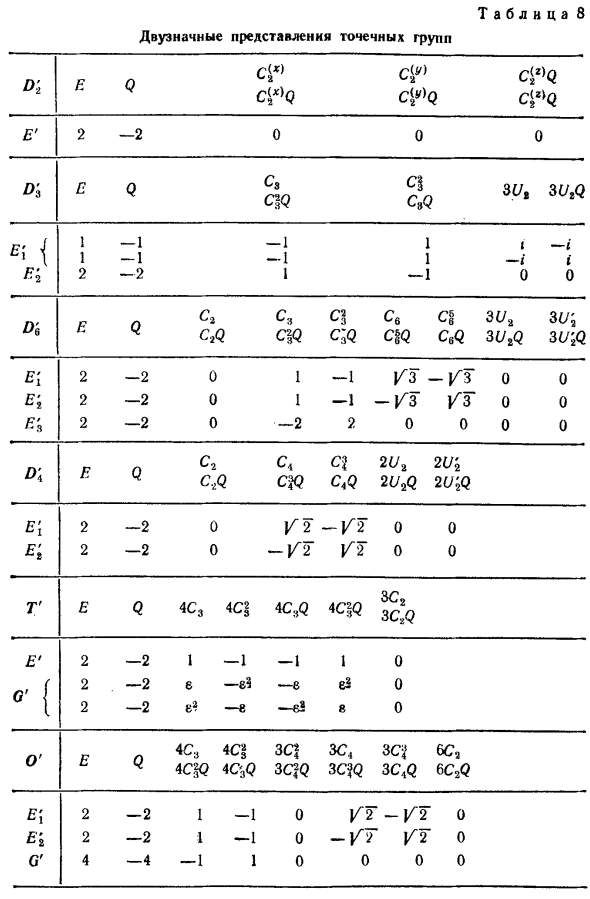
- Выпрямление Два комплексных сопряженных одномерных произведения. Найдите выражение группы T, два других выражения Ния. Аналогичные рассуждения Проехать здесь, и вы найдете выражение группы O ‘. В итоге Tab. 8 дается характер перечисленного двойного представления Группа (только выражение, соответствующее 2 Значимое представление нормальной группы). Тот же вид У них двойная группа одного типа.
2 по той же причине, что и обычный вид Комплексное сопряженное двузначное представление Рассматривается как одно физически неприводимое представление Двумерный. Одномерный двузначный Даже если символ является действительным числом, выражение должно быть удвоено Это реально.
Остальные точечные группы Или в результате прямого умножения на Представление последней группе С особым расчетом. Людмила Фирмаль
Факт проблемы (см. § 60) относится к системам с полуцелыми спинами. Комплексная сопряженная волновая функция линейно независима Мы есть Так что, если у вас есть двузначное одномерное представление Группа, включающая материал персонажа 1) Функция φ), но комплексная сопряженная функция φ.
Преобразовано в эквивалентное представление, все возможно Однако мы настаиваем на том, что φлφ * линейно независима. с того времени г) C’n группа с нечетным числом ni имеет такое выражение. x (Cn) = равно, а комплексная сопряженная волновая функция Если это так, они должны принадлежать к одному и тому же уровню энергии В физических приложениях вы можете увидеть это Должен быть удвоен.
Все упомянутое в § 97 о том, как найти правила отбора Различные физические величины / матричные элементы вычетов Действительно для систем с полуцелыми спинами. Только диагональные (энергетические) матричные элементы Милиционер. Рассмотрите и повторите аргумент, приведенный в конце §97. На этот раз в случае формул (60.2) и (60.3)
Если четное или нечетное относительно обращения времени, Нахождение правила выбора должно рассматриваться соответственно Антисимметричный {D} или симметричный [D] Выражение выражения >> («) само сравнивается наоборот Действительно для si в правилах, описанных в § 97 Спин целое число 1). Решите, как разделить атомные уровни (используйте данные) Общее значение момента J Симметрия О 2).
Волновая функция состояния атома с определением момента J и времени Личная ценность M j выполняет неприводимое из (2 J + 1) измерений Настройка группы O с символами, определенными в выражении (98.3). малина Поместите это выражение в неприводимую часть (как правило, ясно, J или половина целого числа из двух цифр J), тем самым решая надежду Отдел (ср. § 96).
Перечислите неприводимые части представления Соответствует первым нескольким значениям J. J = 0 1/2 1 3/2 2 5/2 3 Ar E (f i G ‘E + F2 E’2 + G’ A 2 + Fi + F2 г) в случае двух цифр в связи с применением настоящих правил Выражения и отдельные выражения не включены симметрично, Антисимметричный продукт самовыражения.
Для двоих Произведение {D (a) 2}, важное представление размерности 2, просто Падать с одного. 2) Например, можно говорить об атомах в кристаллической решетке. для Кроме того, наличие или отсутствие центра симметрии Метрика для внешнего поля вопроса не важна, Поведение волновой функции при инверсии (четное или нечетное) Уровень) не связан с моментом J.
Смотрите также:
| Правила отбора для матричных элементов | Классификация молекулярных колебаний |
| Непрерывные группы | Колебательные уровни энергии |
Если вам потребуется заказать решение по физике вы всегда можете написать мне в whatsapp.

