Двухполостный гиперболоид
Пусть поверхность задана уравнением
Если поверхность (12.31) пересечь плоскостями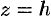 
, то линия пересечения определяется уравнениями
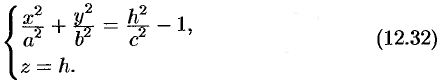
Отсюда следует, что:
а) если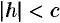 
, то плоскости 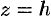не пересекают поверхности;
б) если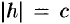 
, то плоскости 
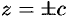касаются данной поверхности соответственно в точках 
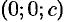и 
.
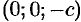в) если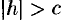 
, то уравнения (12.32) могут быть переписаны так
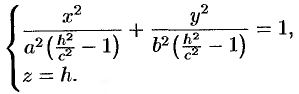
Эти уравнения определяют эллипс, полуоси которого возрастают с ростом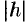 
.
Пересекая поверхность (12.31) координатными плоскостям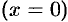и 
и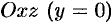 
, получим в сечении гиперболы, уравнения которых соответственно имеют вид
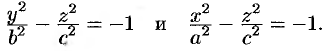
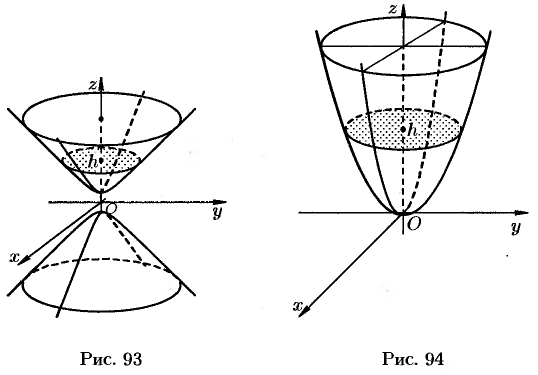
У обеих гипербол действительной осью является ось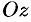 
. Метод сечения позволяет изобразить поверхность (см. рис. 93), определяемую уравнением (12.31), как поверхность, состоящую из двух полостей, имеющих форму выпуклых неограниченных чаш. Поверхность (12.31) называется двухполостным гиперболоидом.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Эллипсоид |
| Однополостный гиперболоид |
| Эллиптический параболоид |
| Гиперболический параболоид |
