Оглавление:









Двухмерная стационарная теплопроводность
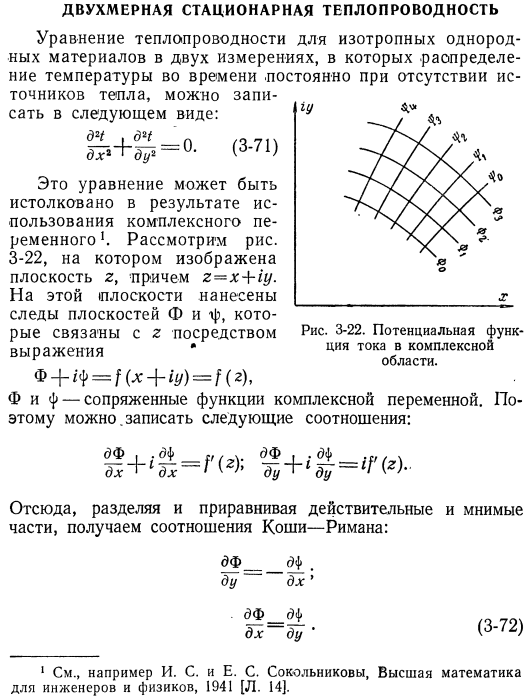
- Уравнение теплопроводности для 2-мерного изотропного однородного материала. Распределение температуры во времени является постоянным заочно. Источник тепла можно описать следующим образом: (w-Х1) Это уравнение можно интерпретировать как результат использования комплексной переменной. 3-22, z = x + iy показывает плоскость z. Эта плоскость имеет трассировку плоскостей f и-f, которые связаны с z формулой f. φ +φφ= /(^ + ‘/)= /(2).
Рисунок 3-22. Потенциальная текущая функция в сложном регионе. φ и φ-сопряженные функции комплексных переменных. Таким образом, можно записать следующие отношения: Df_ _ df. Do это. ДТ__д±ДХ-ду ’ (3-72) 1 например, И. С. И Е. С. Сокольниковы, высшая математика для инженеров и физиков, 1941 [Л. 14]. * Следовательно, трассировки Ф= const и ф= const ортогональны друг другу. То есть перпендикулярно друг другу на пересечении. Другая 1 характеристика сопряженной функции заключается в том, что каждая из них удовлетворяет уравнению Лапласа.
Таким образом, деление и уравнивание действительной и мнимой частей дает отношение между Коши и Риманом. Людмила Фирмаль
Это свойство может быть обозначено дифференцированием выражения (3-72) на части, сначала по отношению к x, затем к y, следующим образом: ^ 2Ф _ d2f _d ^ dh dh 2 dhdu du2 И затем d2f, d2f, d2f_, д2б. Du2 ’ДХ ду ДХ ду dh2′ Из этих соотношений мы получаем 2 уравнения Лапласа. 02ф (? Ф. Dh2, t, du2 ’ л. Dh2 ’du2′ (3-73) Если предполагается, что φ= /указывает температуру, то φ должно быть связано с q*, поскольку оно должно указывать на тепловой поток. Давайте рассмотрим фотографию. На рис. 3-23 показана система координат$, n. N перпендикулярно изотермам, а s касательно к изотермам в той же точке.
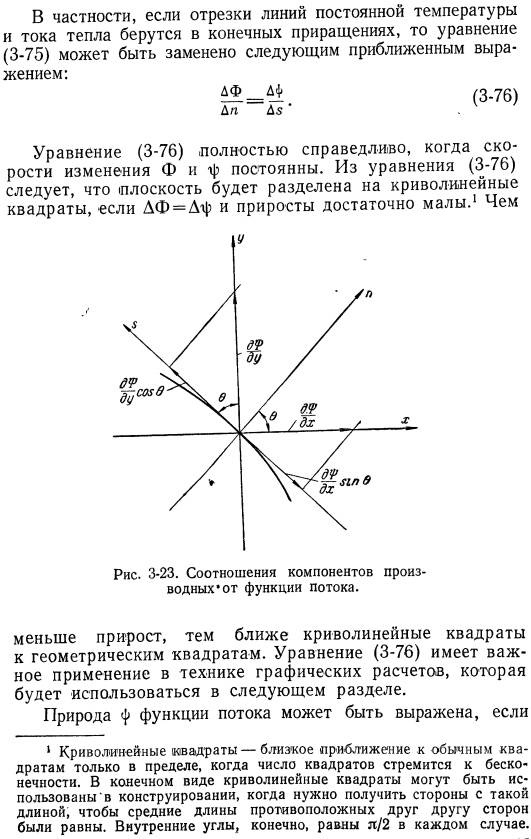
Тепловой поток, направленный вдоль n, можно описать следующим образом: в ДФ. Использование df — _d, cₒₛ0 _ _ x sin 0. ДФ * ДП» Если эти условия используются по отношению к выражению (3-72), то это выражение имеет вид: — 2С = — Лc⁰s⁰isⁱⁿ ^ =-• (3-74) [Уравнение (3-74) показано на рис. От 3 до 23. [] Поэтому ДП ДС ’ (3-75) * Сопряженная функция уравнения Лапласа обычно называется потенциальной функцией и функцией потока. Здесь это соответствует температуре и тепловому потоку соответственно. В частности, если отрезок прямой постоянной температуры и теплового потока получается с конечным шагом, то формулу (3-75) можно заменить следующей приближенной формулой: Жизнь: lf-lf. (3-76) ДП Д $. 7.
Формула (3-76) совершенно справедлива, когда скорость изменения φ и φ постоянна. Из Формулы (3-76) следует, что если рост достаточно мал при df = df, то плоскость разбивается на квадраты кривой. Рисунок 3-23. Доля производной * компонента функции потока. Чем меньше коэффициент усиления, тем ближе изогнутый квадрат к геометрическому квадрату. Формула (3-76) имеет важное применение для графического метода расчета, используемого в следующем разделе. Характер функции потока φ равен 1 1 изогнутый квадрат-приближение, близкое к обычному квадрату, только если число квадратов стремится к infinity. In окончательную форму, изогнутый квадрат можно использовать в строительстве, когда необходимо получить стороны такой длины, чтобы средняя длина противоположных сторон была равна друг другу.
Конечно, внутренний угол будет равен 1/2 в каждом случае. Рассчитайте тепловой поток, проходящий через основную зону (рис. 3-24): dqₓ= — зл ^ -ды = — зл ^ -ды, (3-77) Где l-размер, перпендикулярный плоскости чертежа. Используя формулу (3-72) для интегрирования формулы (3-76) по высоте ({/a— / l), это выглядит так: Вау. Что? , = — j ^ = — u j-й ay = — on-w- Это здорово. Это здорово. Подобный этому — что? Г = — ДФ (3-78) Или текущая функция f принимает следующий вид: Ф=ЛГ- (З-⁷⁹) Таким образом, функция потока φ представляет собой суммарный тепловой поток, рассчитанный для каждой единицы теплопроводности и для единицы глубины. Когда f постоянна, величина теплового потока q Является постоянной, а поверхность, представленная линиями f1 и f2, q образует постоянный тепловой поток трубки. Графическое изображение потока. Вышеупомянутое содержание последнего абзаца может быть использовано для решения стационарной задачи теплопроводности в 2d, используя метод, известный как графическое отображение потока.
Этот метод основан на свободной руке эскиза обтекаемой (streamline) и потенциальной линий, согласно правилам, относящимся к квадратуре квадрата кривой. Таким образом, сетка линий тока или фи потечет. Ниже приводится описание этого метода. Представьте себе коробку (рис. 3-25). Верхняя и нижняя поверхности имеют постоянную температуру t1 и 6 соответственно, остальные поверхности полностью изолированы. Верхняя поверхность может быть полностью удалена с образованием любого количества проходов в тепловом потоке (токовой трубке).
Линии, которые рисуют изотерму, могут быть нарисованы интервалом a / / » ar / = ax и ортогональными условиями изотермы и линии (теплового потока на их пересечении. Тепловой поток через трубку теплового потока БК = — uax- ^. (От 3 до 80) Выражение (3-80) может быть записано так же, как выражение (3-78) для условия Дг/ =дх. — (3-81) Необходимо продолжать строительство до тех пор, пока поле потока не будет exhausted. As в результате, существует nc ток трубки, n temperature температура a / rise. Весь тепловой поток в организме, по-видимому, является суммой роста теплового потока за счет общей разности температур. _9_—^ ы- (т _____ /) l«nbyby (3-82) Здесь, / j > t₂. При построении использовался dx = at /;. Отсюда = (3-83) Отношение nc / nr = t-это коэффициент формы объекта.
Форм-фактор тела-это чисто геометрическая величина, которую можно определить только один раз для любой заданной вещи 1 термин «форм-фактор» часто используется при изучении теплопередачи и каждый раз имеет разное значение, так что читатель может легко понять это. Общим для всех форм-факторов является определение geometry. So, в каждом отдельном случае он определяется только один раз для каждого рассматриваемого органа. Система.
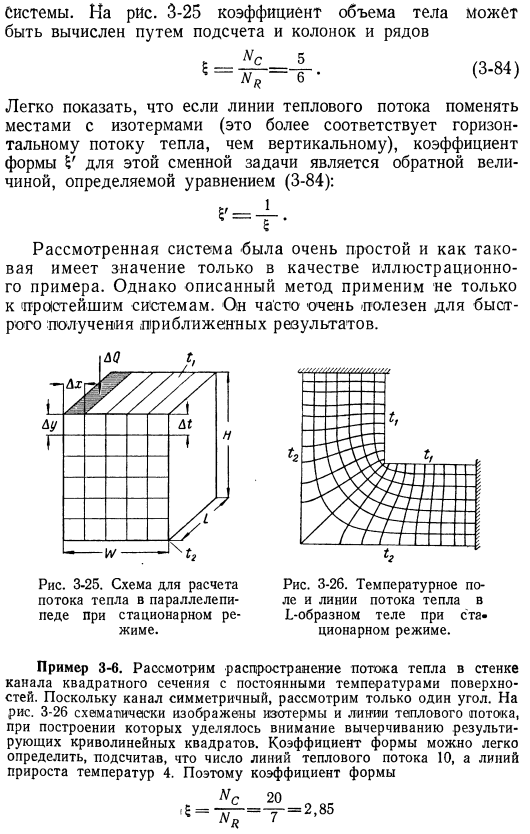
Рис. 3-25 соотношение объема тела может быть рассчитано путем подсчета как столбцов, так и строк nᵣ5 < 3-м> Легко показать, что коэффициент формы v для этой взаимозаменяемой задачи является обратным, определяемым формулой (от 3 до 84), когда тепловой поток обменивается с изотермической линией (это соответствует горизонтальному тепловому потоку, чем вертикальному направлению). : Рассмотренная система достаточно проста, поэтому заслуживает лишь в качестве наглядного примера. Однако описанный метод (он применяется не только к самым простым системам, его можно применять только в самых сложных случаях). Часто бывает очень полезно быстро получить приблизительный результат. Рисунок 3-25.
Предложена схема расчета теплового потока параллелепипеда в стационарном режиме. Рисунок 3-26. Температурное поле и тепловые линии течения Г-образного тела в стационарном состоянии. Пример 3-6 рассмотрим распространение теплового потока на стенке квадратного канала с постоянной температурой поверхности. Поскольку канал симметричен, рассмотрим только 1 угол. На рис. 3-26 представлено схематическое представление Изотерм и линий теплового потока, на структуру которых обращено внимание при нанесении полученного криволинейного квадрата. Форм-фактор может быть легко определен путем вычисления 10 линий теплового потока и 4 линий повышения температуры. Следовательно, фактор формы КС 20. 2. 85 ’5 = 7.
И тепловой поток, передаваемый за счет теплопроводности, q = 2. 85 x£ (/, -/.). Тепловой поток можно рассчитать, зная свойства материала, из которого изготовлены стенки канала и перепад температур по толщине стенок1. Рисунок 3-27. Система координат релаксационного метода. Релаксационный метод. Решение двумерного уравнения теплопроводности с источником тепла или без него представляет собой численный метод, разработанный Саутвеллом[l. 16, 17, 18], называемый релаксационным методом. Этот метод (в основном используется для решения уравнения Лапласа-Пуассона, но обсуждение здесь связано с проблемой теплопроводности.
- В стационарных режимах без внутреннего источника тепла уравнение Лапласа является дифференциальным уравнением, решение которого определяется в результате с учетом соответствующих граничных условий. Поле в корпусе без источника тепла: — y + > = ° — (w — ⁸⁵ ) Рассмотрим точку* * п (х, г) тела, через которые проходит декартовой системы координат (рис. 3-27). Другими точками этого тела являются: p (x — — yy), p (x, y — — a), p (x-a, y), p (xy y-a). Для удобства они пронумерованы 1, 2, 3 и 4 соответственно. Если вы знаете температуру точки p (x, y), вы можете использовать ряд Тейлора для вычисления температуры окружающих точек с произвольной точностью. Например, если взять точку p (x, y) как ноль, то она выглядит так: З«+ (^-) ₀a + 4+©•• (3-86) 1 существует множество методов, основанных на сходстве теплопроводности и электропроводности, расхода жидкости и др.
Это может быть использовано для получения графического изображения желаемой формы или для приблизительного определения коэффициента формы. Наиболее распространенной из этих систем является p. j. schneider, «теплопроводность», ch. 13. 45] *. *Есть русский перевод. Пожалуйста, обратите внимание Третий Если вы объедините уравнение (3-86) с (3-87), вы получите: ^ + Г = 2 /₀+ (^ а! + О (а ’), (3-88) Где o (a⁴) обозначает остаточный член порядка a⁴. Выражение (3-88) может быть явно записано в (d2t/dx2) ₀. Члены Для создания новой папки можно использовать следующую команду Подобный. < М + Г −2 / МО » 2 + О.) * (Уравнения, основанные на уравнениях Для Сумма этих 2-х производных дает решение уравнения Лапласа с точностью порядка a С. М. Ommod2 (3-89) ’Решение уравнения температуры/ для (3-89) выражается температурой окружающих точек, находящихся в равновесии /» = * + * «+ ’»-И*. (3. 90) ).
Рассматривая рисунок 3-27 снова в свете уравнения (3-91), когда температура изменяется на 1, оставшееся qo может измениться±1 Людмила Фирмаль
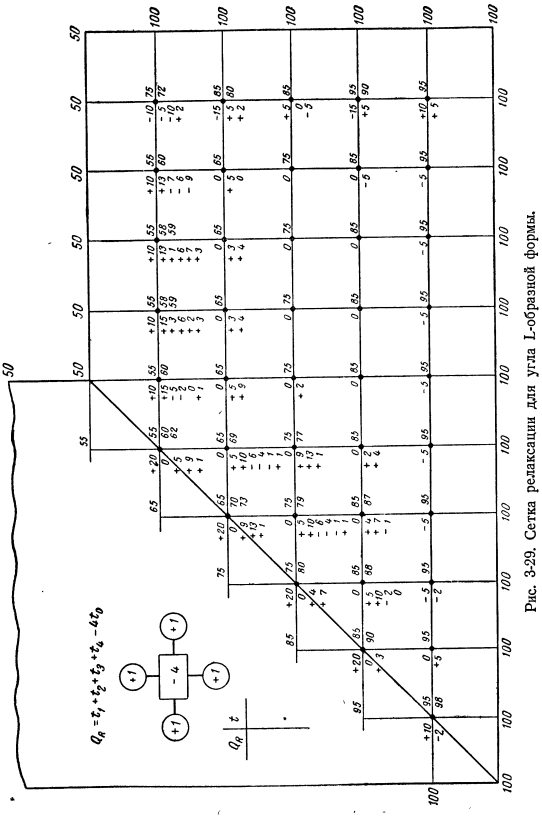
Целью данного метода является установление такого температурного поля на теле, причем его температурное поле удовлетворяет формуле (3-90). Для этого систематически определяют избыточное qₒ. Qо-ТИ + ^ 2 +t₃+ (3-91) И задача обнуления остатка для каждой точки тела сводится к минимуму. Но когда температура самой точки изменяется на 1, оставшееся qo изменяется±4. It есть Ключ к вычислениям. На рис. 3-28 показана удобная модель смягчения последствий. Следующий простой пример полностью описывает этот»процесс». * Пример 3-7. As примером того, как это сделать, рассмотрим l-образный угол. Такой угол показан на рисунке. 3-29.
Температура границ стен является постоянной. Начальное распределение температуры Принимаются соответствующие граничные условия. Величина распределения температуры показывает кадр из узла. Следующим шагом является вычисление остатков для каждого узла с использованием соответствующей модели релаксации*. Это модель уравнения Лапласа в данном случае, потому что нет источника тепла. Остатки появляются слева от узловой точки. Воздействуя на самый большой остаток, он перемещается от точки к точке, изменяя температуру, чтобы уменьшить остаток. Рисунок 3-28. Схема расчета методом релаксации уравнения Лапласа. В этом случае не стоит стремиться точно установить temperature. As при экспериментальной работе навык приходит с практикой.
На рисунке показаны некоторые начальные расчеты, иллюстрирующие этот подход. Из-за симметрии, расчеты были сделаны только около половины угла. Если рассматриваемый объект имеет источник тепла, то уравнение теплопроводности принимает вид уравнения Пуассона. ——— x. ———- С. )- (3-92) Если мы снова используем частичное выражение, оно выглядит так: А + г + ^ 4-4/₀. — ДГ — — — — — — — + О (А *) = Ф (Х, г). (3-93) Остаток qₒ в этом случае игнорирует 4-е или более высокие члены и принимает следующий вид: ^ o =Л4- / ₂4 — ^ 4 — ^-4 /о-а2/ (x, y). (3-94) Для выражения (3-94) необходимо изменить модель смягчения, как показано на рисунке 5. 3-30 отображает термин a2f (x, y), который характеризует рассеивание тепла. Очевидно, что источник тепла может быть произвольно распределен по всему телу, и это распределение представлено точками при расчете. Таким образом, источник тепла является своеобразной коррекцией эффекта изменения в нулевых точках. Метод релаксации также может быть использован в цилиндрической системе координат.
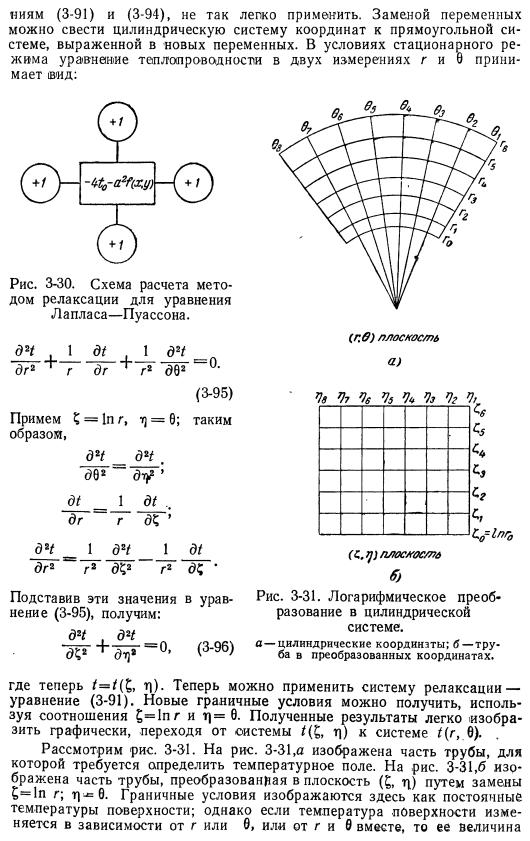
Однако в этом случае уравнение соответствует уравнению Рисунок 3-29. L-образная угловая релаксационная сетка. 0/705 9, 73. А и −6 * /〜И −1. 1 Около 75 0 Ниям (3-91) и (3-94) не так легко apply. By подставляя переменные, можно свести цилиндрическую систему координат к прямоугольной системе, представленной новыми variables. In стационарное состояние, 2-мерные g и 9 тепловых уравнений принимают вид: Рисунок 3-30. Релаксационная схема уравнения Лапласа-Пуассона. Д’t1 д /■1d2t рп2⁺г д-р⁺g2602°* (3-95) Вы принимаете это? = g, t] = 6; Вот так Д2/ _d2t. 692dt? * ДТ __ ДТ 1 ДГ г ДК ’ d’t _ 1d2t1 dt dr2s7r » d52’r2dc * (d. 0) самолет (c, tj) плоский / l б. ) Рисунок 3-31. Логарифмическое преобразование в цилиндрической системе. А-цилиндрические координаты; б-трубы преобразованных координат. Если подставить эти значения в Формулу (3-95), то получим: Д2/. Д2Т. Дв ^chj2 «»⁰ ⁰f3″⁹⁶) Здесь/ / / (ξ, η) -можно применить релаксационную систему-уравнение (3-91).
Новые граничные условия могут быть получены с использованием ξ=1πη и η=. Полученные результаты можно легко выразить графически, передав их из системы / ξ (η) в систему/ (r, 0). 。 Давайте рассмотрим фотографию. 3-31. На рис. 3-31 показана часть трубы, необходимая для определения температурного поля. На рис. 3-31. 6 показан участок трубы, преобразованный в плоскость (£, l) путем замены£= 1n g. L — ^ b-граничное условие изображено здесь в виде постоянной температуры поверхности. Однако, если температура поверхности изменяется в соответствии с r или 0, или r и 9, ее значение На границе точка (£, 7]) соответствует той же точке преобразования на плоскости. Вы можете рассчитать температуру каждой точки, применив прямоугольную релаксационную сетку непосредственно к шаблону плоскости (£, m|).
Поскольку это уже установлено, значения температуры этих точек связаны с точками на плоскости с помощью членов преобразования (r, 6). Поэтому проблема решена. Задачи 3-1. Напишите уравнение для зависимости длины температурного поля конического ребра. Основание конического ребра имеет радиус b и угол a на вершине. Температура основания считается постоянной. 3-2. Измерения, выполненные с помощью серии термопар, установленных на полубесконечном теле в направлении теплового потока, проводятся с помощью ДТ! Dx s) и d2t / dx2 0. Какие выводы можно сделать из этих экспериментальных наблюдений? 3-3. Они предложили нагревать воду с помощью калорифера диаметром 2, 5 мм и длиной 71 см на 2 киловатта. * Степень h, температура воды и выход 60°c Могу ли я использовать медную оболочку? 3-4. Трубы диаметром 20, 32 см прокладываются на глубине 76, 2 см от поверхности Земли.
Температура земной поверхности составляет 4, 4°c, температура стенок трубы-83, 5°c. С помощью графического дисплея потока можно определить устойчивый тепловой поток от трубы к земной поверхности. Сравните результаты этого измерения с результатами, полученными в результате расчетов. 3-5. Количество стекловаты и минеральной ваты требуется для утепления так, чтобы температура печи на кухне не превышала 58°с. Максимальная температура печи поддерживается термостатическим регулированием и достигает 288°с 3-6. Стенки холодильника утеплены стекловатой толщиной 7, 62 см, которая расположена между наружной и внутренней стенками холодильника. Поверхность внутренней стенки вблизи испарителя составляет 6, 6°С. Показания термометров, установленных на наружных стенках、 40, 7 ккал / м2-ч -, температура окружающей среды 32, 2°c Эффективна ли теплоизоляция? Если нет, то это указывает на причину низкой эффективности. 3-7.
Балка с прямоугольным поперечным сечением 100×6. 35 Х25. 4 мм, что очень долго по сравнению с другими измерениями, в которых течет ток, определяет температурное поле для установившегося режима. Балка изготовлена из меди и имеет температуру окружающего воздуха 18, 3°С. 3-8. Рассчитайте теплопередачу через стенки кругового цилиндра с эксцентрическими каналами. Наружный диаметр 20, 32 см, внутренний диаметр 12. 7 см, эксцентриситет 2, 54 см. Внутренняя температура поверхности составляет 121 ° с, наружной поверхности составляет 30°С.
Материал цилиндра является токопроводящей, не изолируя. 3-9. Завершите решение задачи, показанной на рисунке. 3-29. 3-10. Определить стационарную температуру нуля в любой точке p (t, 0) длинного стержня радиуса r. Половина поверхности хранит температуру tₐ при 0 6 l, а другая половина хранит температуру 0 2π.
Смотрите также:
| Стенка с внутренним источником тепла | Переходные процессы теплопередачи |
| Подземный кабель | Периодический перенос тепла |

