Оглавление:






Движение жидкости в трубе
- В стабильном потоке » толщина пограничного слоя равна радиусу трубы. Поэтому в формуле вместо значений скорости uₛ и температуры tₛ » необходимо применять значения скорости и температуры, которые выполнены вдоль оси трубы. Однако коэффициент теплопередачи может быть определен по средней интегральной температуре/ в, и в Формуле (8-12) применяется среднее значение скорости. Это не совсем правильно, но ошибка небольшая.
Если напряжение трения определяется по формуле (6-50), а отношение скоростей определяется по формуле (6-51), то последняя формула принимает вид: _ «0, 0396 (uₘdm⁴/ м я; + а(uₘdm⁸ (ПР-1) Постоянная А равна 2. 44. Однако по сравнению с экспериментальными результатами для вязких жидкостей это значение слишком велико и, кроме того, a является функцией критерия Прандтля. Рисунок 8-4, v. byun [l. 99]. Левое выражение формулы (8-13) эквивалентно эталонной формуле nud / (redpr). Эта величина называется критерием Стэнтона и обозначается символом Св.
При таком определении количества теплоты первое начало становится содержательным законом, допускающим экспериментальную проверку, так как все три величины, входящие в выражение для первого начала, могут быть измерены независимо. Людмила Фирмаль
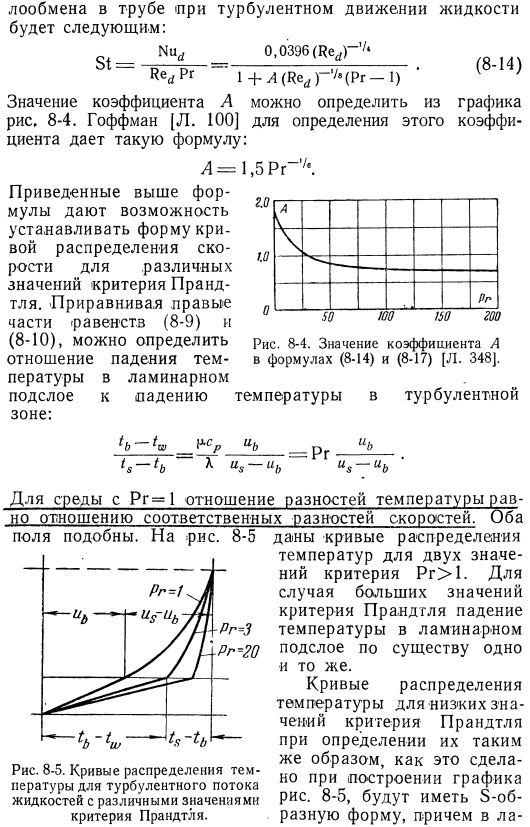
Таким образом, в окончательном виде тепла Обмен трубы при турбулентном движении жидкости происходит следующим образом: Ну, 0. 0396 (ре^ — л + ^ (красный) -/. (Пр-л) ’ Значение коэффициента а можно определить из графика на рис. 8-4. Хофман. 100]для определения этого коэффициента приведем следующую формулу: Приведенное выше уравнение устанавливает форму кривой распределения скоростей для различных значений критерия Прандтля. При уравнивании правой части уравнения (8-9) и (8-10) 、 РГ. I7100150200 Рисунок 8-4. Значения коэффициентов а Формулы (8-14) и (8-17) [l. 348].
Ламинарный поток в час Подслой падения температуры турбулентной зоны: Для среды с pr = 1 отношение разности температур равно отношению соответствующей разности скоростей. Оба поля похожи. Рисунок 8-5 Рисунок 8-5. Кривые распределения температуры турбулентности с различными опорными значениями Прандтля. Кривая распределения температуры приведена для 2 значений стандартного pr> 1. Если значение критерия Прандтля велико, то падение температуры ламинарного подслоя по существу одинаково.
Кривая распределения температуры 8-5 нижних значений критерия Прандтля при их определении выполняется так же, как и при построении рисунка, в s-образной форме, в виде линии Если подслой мал, то повышение температуры незначительно, а максимальная разница температур связана с турбулентной зоной. Это связано с очень низким тепловым сопротивлением слоистых подслоев, по сравнению с тепловым сопротивлением турбулентной зоны. Однако на практике дело обстоит иначе happens. In турбулентный поток, конвективный теплообмен накладываются на теплообмен.
Для среды с критерием Прандтля 1 или более теплопроводность мала по сравнению с конвективным переносом тепла, поэтому она игнорируется в приведенных выше расчетах. Однако в ограниченном случае конвективная теплопередача уже незначительна, но теплопередача за счет теплопроводности является главным фактом, хотя значение стандарта Прандтля невелико, оно будет иметь равное или большее значение. Расчеты, выполненные в разделе 7-7, обычно дают хорошие результаты.
Общие сведения о теплопередаче жидкости или газа при прохождении pr — > 0 через трубу, когда параболическая кривая распределения скоростей, используемая в ламинарном потоке участка 7-7, заменяется турбулентной кривой распределения скоростей. Достаточно хороший результат может быть получен, если кривая распределения скорости турбулентности аппроксимируется кривой постоянной скорости (шлаковый поток).
При установившихся тепловых условиях и постоянном тепловом потоке вблизи стенки эта операция приводит к соотношению nud = 8. At постоянная температура стенки-отношение nuj = 5, 8 против. Более подробная информация о теплопередаче жидкого металла будет рассмотрена в разделе 10-4. Это очень удобно для расчетов теплопередачи, если в левой части уравнения (8-14) находится комбинация эталонных величин nuj, rej и pr.
Количество тепла, передаваемого на стенку трубы длиной l, равно следующему. Вопрос = azdl (^ в-у- Это количество тепла также может быть выражено падением температуры жидкости от температуры на входе. Температура на выходе tₑ Если вы сделаете некоторые преобразования, приравнивание права на эти равенства выглядит следующим образом: Но. .RedPr-tₙ-тю (8-15) Это соотношение можно использовать для расчета температуры жидкости .
Когда вы выходите из трубы, если вы знаете размеры трубы, вам нужно воспользоваться логарифмическая средняя температура жидкости при входе в трубу и на выходе из трубы, вместо того, чтобы температура жидкости на входе в трубу, температура TW стенки трубы, и значение НСЖ / (RedPr) эталонного комплекса При выводе формулы (8-12) предполагалось, что физические параметры не изменялись .Э . Гофман . 101] исследовано влияние изменчивости физических параметров на теплообмен .
- Он установил, что формула (8-14) справедлива только в том случае, если физические параметры взяты из определенной температуры . 0 .1 РГ 4-40 В, Л, Г- С РГ 4-72 (8-16) Для газа (Pr = 1) это уравнение приблизительно дает t среднее арифметическое между температурой среды и температурой ее стенок .Чем больше критерий Прандтля, тем ближе значение f *к значению средней температуры жидкости, то же самое относится и к температуре tb между слоистым подслоем и зоной турбулентности (рис .8-5) .
Такое определение температуры является лишь функцией Pr, которую следует рассматривать как начальное приближение, поскольку предполагается, что теплопередача жидкости с переменными свойствами зависит от того, как эти свойства изменяются в зависимости от температуры и давления .В качестве охладителя реактора используется вода сверхкритического давления .Теплообмен вокруг критического давления характеризуется тем, что физические параметры, в частности удельная теплоемкость, сильно изменяются с температурой .Р . Г . Деслер . 102]и К .Гольдман . 103] рассчитано трение и теплообмен с водой, протекающей в турбулентности по трубе при давлении 775 при давлении см2 .Были приняты установленная скорость и распределение по температурам .
Результаты его расчетов могут быть аппроксимированы с помощью постоянного отношения свойств. Людмила Фирмаль
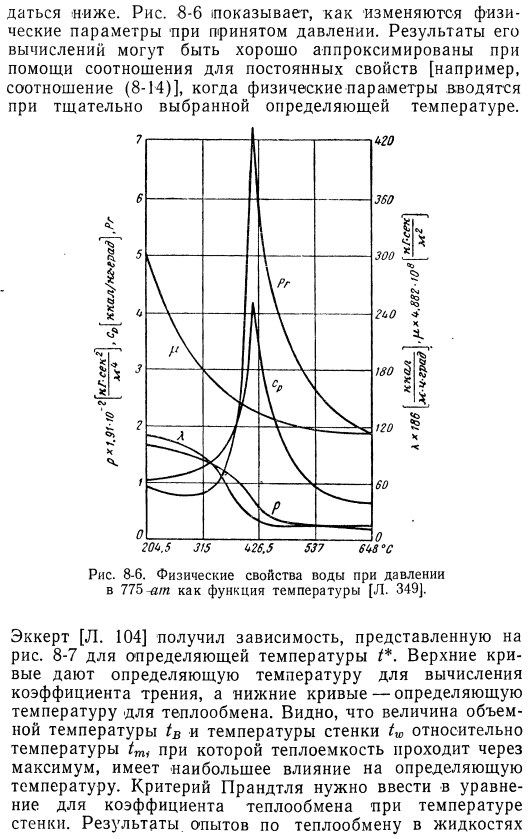
В этом разделе описываются результаты расчета расслоения Это показано ниже .Рисунок 8-6 показывает, как физические параметры изменяются с полученным давлением .[например, соотношения (8-14) ], если физические параметры вводятся при тщательно подобранном решении температуры .Рис .8-6 .Физические свойства воды при давлении 775 в зависимости от температуры[L .349] .Эккерт . 104] получены зависимости, показанные на рисунке .8-7 / *для определения температуры .
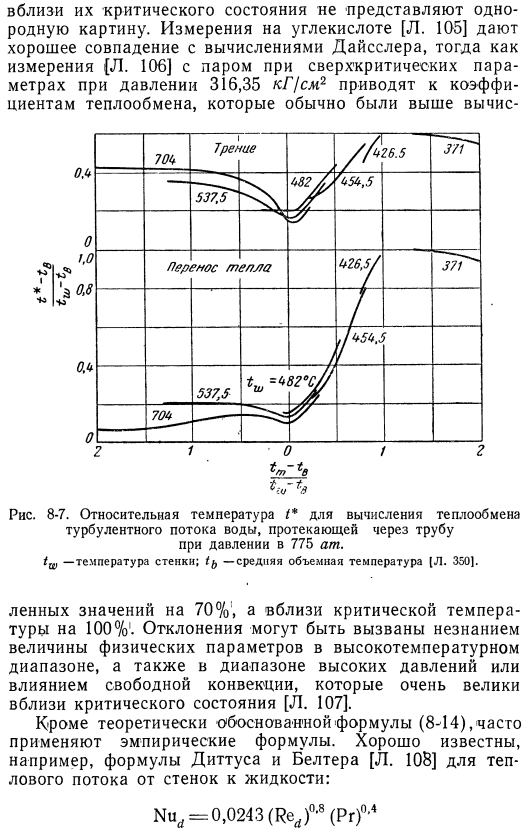
Верхняя кривая показывает температуру решения для вычисления коэффициента трения, а нижняя кривая показывает температуру решения для тепла transfer .It видно, что значения объемной температуры (tB) и температуры стенки (tw) для температуры, при которой теплоемкость проходит через максимальное значение (t1), оказывают наибольшее влияние на определяемую температуру .Критерии Прандтля должны быть введены в уравнение коэффициента теплопередачи при температуре стенки .Экспериментальные результаты по теплопередаче жидкостей Вблизи своего критического состояния они не представляют собой единой картины .Измерение углекислого газа[L .[105] хорошо согласуется с расчетом disslar .
С другой стороны, давление (316, 35 НГ /sls2) измеряется в сверхкритическом параметре пара (L .106) обычно приводит к более высокому коэффициенту теплопередачи, чем расчет .Рис .8-7 .Рассчитайте турбулентный теплообмен воды, протекающей по трубе при относительной температуре/ * давлении 775 Ат .tw-температура стенки; — средняя объемная температура[L .350) .Значение 70%, вокруг критической температуры 100% .Отклонения могут быть вызваны незнанием величины физических параметров в высокотемпературном и высоконапорном режимах или влиянием очень большой свободной конвекции вблизи критического состояния[L .[107] .
Помимо теоретически обоснованной формулы (8-14) часто используются эмпирические формулы .Например, Dittus и Belter [L .108]тепловой поток от стенки к жидкости: Nud = 0 .0243 (красный) ⁰ ’ ⁸ (Rg) ⁰, ⁴ Nuᵣf= 0 .0265 (красный) ⁰ ’ ⁸ (Prf3 -Для теплового потока от жидкости к стенкам .Использование 2 различных формул в случае нагрева и охлаждения[L .109] не считается полностью удовлетворительным .Если турбулентность полностью стабилизирована, то эти зависимости обеспечивают точное results .In на участке стабилизации значение коэффициента теплопередачи может быть несколько больше расчетного .Х . Хаузен . 110] показано следующее уравнение .
Для среднего значения критерия Нуссельта Nuᵣf= 0, 116 ( (Reᵣf-125] (₽•) ■ ’*X X 1 + Где tsv-вязкость при средней интегральной температуре жидкости, а qiu-вязкость при температуре трубы wall .In кроме того, физические параметры должны быть определены в тб .Эта формула учитывает условия, которые существуют при стабилизации zone .It также дает удовлетворительные результаты для переходных зон со значением Rej от 2300 до 6000 .Предполагается, что это соотношение применяется к жидкостям (маслам), в которых преобладают колебания вязкости .На рис .8-8 показана область перехода по результатам эксперимента, проведенного Зигером и Тейтом[L .[111] .
Уравнение Хаузена показывает средний коэффициент теплопередачи в области между начальной точкой и точкой x нагревательной части трубы .Локальный коэффициент теплопередачи может быть получен из этой зависимости путем дифференцирования .Когда вы делаете это, термин в скобках равен 1 + (!) ./ ₃) (//Х) при замене на 2/з ясно, что то же соотношение представляет собой локальный критерий нуссельта .Ж .эксперимента гранат[л .. .] 112]и расчет Р . Деслер .Из указывает, что коэффициент теплопередачи жидкости в порядке критерия Прандтля 1 или более уменьшается с увеличением длины x, даже быстрее, чем указано этим formula .At при длине 15 в диаметре локальный коэффициент теплопередачи составляет около 1%от величины, которая достигается асимптотически в длинной трубе .
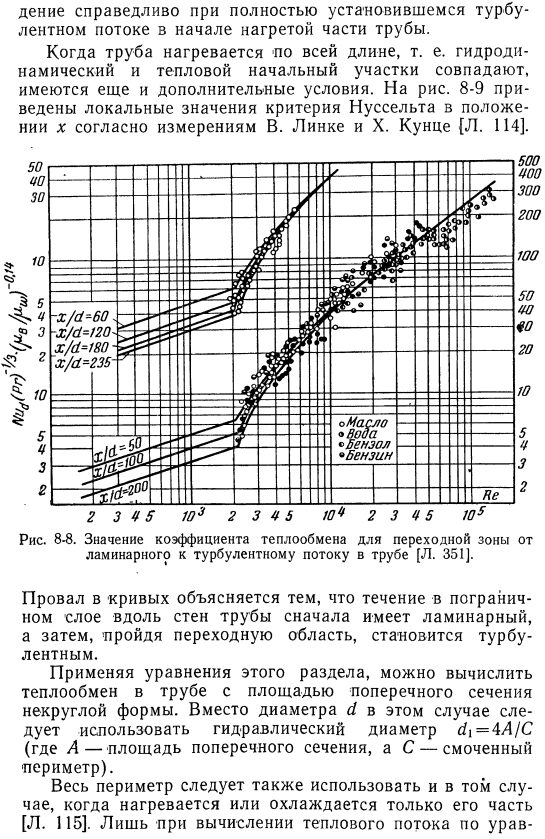
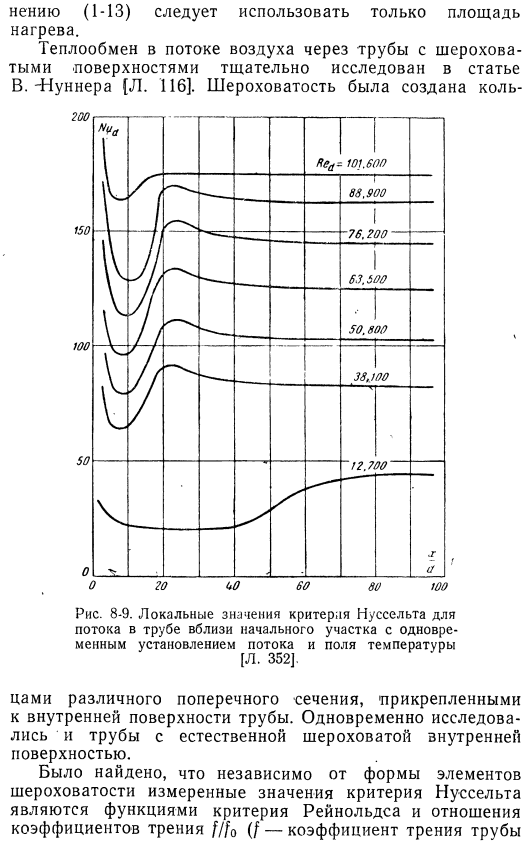
Это заявление Это относится и к идеально устойчивой турбулентности в начале нагретой части трубы .Если трубы нагреваются по всей их длине, то есть гидродинамические и тепловые начальные участки совпадают, то возникают дополнительные условия .На рисунке 8-9 показано локальное значение критерия нуссельта позиции Рис .8-8 .Значение коэффициента теплоотдачи переходной зоны от ламинарного к турбулентному течению в трубе[л . 351] .
Провал кривой объясняется тем, что течение пограничного слоя вдоль стенки трубы сначала имеет ламинарный характер течения, а затем, пройдя через переходную зону, становится турбулентным .Используя уравнения в этом разделе, можно рассчитать теплопередачу в трубе с некруглым cross-section .In в этом случае вместо диаметра d используют гидравлический диаметр cG = 44 / C (A-площадь поперечного сечения, C-периметр смачиваемой детали) .Если нагревается или охлаждается только часть периметра, то следует также использовать весь периметр[L .115] .
Только при расчете теплового потока по уравнению Для варианта (1-13) следует использовать только обогреваемую зону .Теплопередача воздушного потока через трубу с шероховатой поверхностью осуществляется с помощью W . Nunner (L .116), который был тщательно исследован в статье .Рис .8-9 .Локальное значение критерия нуссельта течения в трубе вблизи начального участка с одновременным установлением потока и температурного поля Cts различных поперечных сечений прикрепленных к внутренней поверхности pipe .At тогда же были исследованы и трубы с естественной шероховатой внутренней поверхностью .
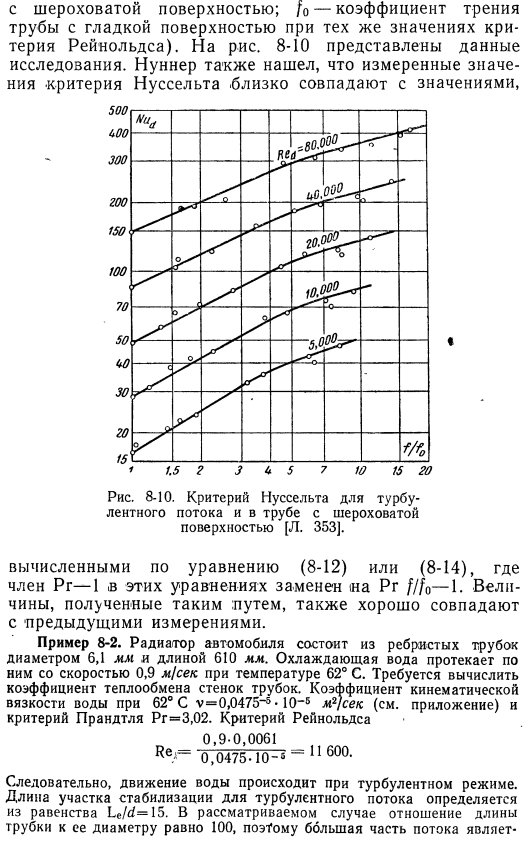
Независимо от формы элемента шероховатости, измерение критерия нуссельта является функцией критерия Рейнольдса и отношения коэффициента трения f / fQ (f-коэффициент трения трубы Шероховатая поверхность; / o-коэффициент трения трубы с гладкой поверхностью при одинаковом значении критерия Рейнольдса .На рис .8-10 представлены данные исследования .Наннер также обнаружил, что измерения критерия Нуссельта были почти идентичны следующим .Рис .8-10 .Ссылка нуссельта в трубе турбулентности и шероховатой поверхности[л . 353] .Он рассчитывается по формуле (8-12) или (8-14) .Вот, термин ПР-1 из этих equations .Is заменен на Pr f / f-1 .
Полученные таким образом значения также хорошо согласуются с предыдущими измерениями .Пример 8-2 автомобильные радиаторы состоят из ребристой трубы диаметром 6, 1 мм и длиной 610 мм .охлаждающая вода течет со скоростью 0, 9 м !Считанные секунды .При температуре 62°C . It необходимо рассчитать коэффициент теплопередачи стенок трубы .Кинематический коэффициент вязкости воды при 62°Cv = 0 .0475 — ⁵ •10 «⁵m2] секунд (см .приложение) и ссылка Прандтля Рг= 3 .02 .Критерии Рейнольдса 0 .9-0 .0061 э ?〜0 .0475-10- ⁵ * «11- Поэтому движение воды происходит в турбулентном режиме .
Длина участка стабилизации турбулентности определяется из уравнения Lc / d = 15 .In в этом случае отношение длины и диаметра трубы равно 100, поэтому большая часть потока составляет Будучи гидравлически устойчивым, расчет можно проводить по формуле (8-13) .График на рисунке показывает, что 8-4 A = 1D Ню_________ 0 .0396 / 11, 600 ^ RedPr⁼14- 1, 5 .2, 02 / 11600 ’/’ ’ = 0 .00194 .Стандарты нуд из нуссельта= 0 .00194-11 600-3 .02 = 68、теплопроводность л = 0 .56 к / сал / мЗ-°С . Так .. Х 0, 56 АЕОН 0061 6, 240 ккал ^Н2-Н-град. На расстоянии длины трубы* / a коэффициент теплопередачи уменьшается от высокого до расчетного значения. Зная значение формулы nud / (redpr), можно легко рассчитать температуру воды. Что? Л 4-0. Шестьдесят один = 0. 00194 =qq₆₆-0. 00194 = 0. 776.
Смотрите также:
| Движение жидкости в трубе | Продольное обтекание плиты |
| Аналогия между количеством движения и теплообменом | Последние достижения в теории теплообмена при турбулентном режиме движения |

