Оглавление:









Движение жидкости в трубе
- Когда стенка трубы, в которой движется жидкость или газ, нагревается или охлаждается, на поверхности трубы образуется термический пограничный слой. Surface. At некоторое расстояние от начального На участке, где заканчивается гидродинамический пограничный слой, толщина пограничного слоя достигает величины радиуса трубы (рис. 6-18). Конец на этом участке границы Место стабилизации. ^Во-первых, рассчитайте теплопередачу в области полной термостабилизации.
Для плиты, кривая распределения по температурам в трубе Это третичная параболическая линия. После этого можно определить РГ. 7-15. Определение распределения температуры участков труб в режиме ламинарного течения. Условие кривизны Кривая распределения температуры около стены. Потому что скорость жидкости в этом слое Тепло не передается конвекцией, потому что оно незначительно. Теплопередача через этот слой обусловлена только теплопроводностью.
Тепловой поток через слой, непосредственно прилегающий к стене, должен быть постоянным. Людмила Фирмаль
Для цилиндрической поверхности шины l и радиусом r (Рис. 7-1-5) справедливо следующее уравнение: q, где y-расстояние от стенки, а r-радиус трубы. R = r-подставим y, а затем разделим это уравнение на если мы получим градиент температуры и производную по y, то получим: d’t _ 1-q _ 1 dtdy2 (r-y) 22nl r-y dy отсюда r / = 0 (стена) (7-26) в В этом случае скорость изменения градиента температуры не равна нулю, как в случае плоской пластины, а связана с упомянутой выше зависимостью самого градиента температуры. Почему? Это связано с тем, что площадь поперечного сечения теплового потока уменьшается по мере увеличения расстояния от стенки трубы, но в случае плоской пластины она остается постоянной.
Для Для выполнения вышеуказанных условий разность температур между стенкой трубы и основным сердечником потока должна быть выражена следующим образом: Уравнение для уравнения (7-26) выглядит так: температура между валом и стенкой трубы составляет в головке 8 долларов. Градиент температуры в этом месте должен быть равен: at ( / = /? : Отсюда и жара Поверхность блока стены трубы и подача в время блока, коэффициент передачи тепла подачи через трубу, обычно средняя температура подачи и Температура стен.
Обычно средней температурой считается температура, возникающая при перемешивании всей массы жидкости после рассматриваемого поперечного сечения. Такие как Температура (называется интегральной температурой и объемной температурой n, обозначается tn -’•. * Уравнение (7-29) определяется уравнением. Температуры [уравнение (7-27) ] и закон распределения скоростей (где uₛ-скорость движения вдоль оси трубы, средняя интегральная температура и По температуре стенки трубы a-l s8qa коэффициент теплопередачи определяется по уравнению ₉ = a (/в-q = a (lb, где a-коэффициент теплопередачи (7-28) ).
Где d-диаметр трубы. Б. Есть справочная форма. Теплопередача к стенке трубы осуществляется Грацем {l. 82], Ка-лендаром [l. 83]и Нуссельтом [l. 84]путем решения дифференциального уравнения equation. To выведите эти уравнения、 Уравнения Навье-Стокса, уравнения неразрывности и уравнения энергии должны быть преобразованы в цилиндрические координаты. Некоторые члены этого уравнения могут быть опущены При особых условиях-местами в цилиндрической трубе — возникает полностью устойчивый поток. Решение уравнения течения очень простое, а установленное Кривая распределения скоростей имеет вид параболы.
Этот тип потока обычно относится к типу потока в пуазей. Уравнение энергии может быть выведено непосредственно из баланса Энергия объемного элемента круглой формы длиной dx, радиусом r и шириной dr расположена концентрически в потоке относительно оси трубы. Тепло передается этому объемному элементу. Теплопроводность и конвекция. Во-первых, рассмотрим радиальную теплопроводность. Ось q-wr. Тепловой поток проходит через кольцевую область 2nrdx на расстоянии rrdx до rrd. Дорога к Для этой кольцевой области на расстоянии r — — dr от оси тепловой поток изменяется на-g-dr = — a2i»/ x4 (r-j -) dr.
Этот термин обозначает разницу в теплоте, исходящей от объемного элемента Тепло проходит через область, соответствующую радиусу r + dr, проходит через область, соответствующую радиусу r и поступает в объемный элемент. Там также может быть тепловой поток в осевом направлении Направление. Однако этот тепловой поток, как ожидается, будет намного меньше и имеет градиент температуры в радиальном направлении, что приводит к тепловому потоку в радиальном направлении. Больше. Поэтому осевая теплопроводность не учитывается при расчете Граца и Нуссельта.
Однако в жидком металле теплопроводность по длине существенно меньше. — Температура влияет на создание поля. — Поэтому в последних расчетах это условие учитывается[л. 85]. Тепло также передается объемным элементам и конвекции. При этом теплообмен происходит только в осевом направлении, а количество тепла, которое остается в элементе объема в результате ввода тепла и его отвода от него, составляет:2itrdr $cₚu^ dx. Для Установившаяся теплопроводность и конвекция должны быть равны. Поэтому i d / dt _tcp dt u dr dr) x dx это уравнение описывает поток энергии и определяет температурное поле.
Граничное условие для этого уравнения: Р = 0 в стенке определяется температура или тепловой поток. При наличии постоянной скорости теплового потока на поверхности трубы (7 ^ = const), баланс энергии жидкости, протекающей по трубе, сразу приводит к выводу, что при определенном свойстве жидкости объемная температура жидкости повышается (повышается) Линейный в направлении flow. In в случае термически стабильного потока это также относится к температуре на любом расстоянии вдоль оси трубы. В зависимости от этого вы можете — =c dx уравнение энергии в этом случае сводится к обыкновенному дифференциальному уравнению о r.
Это простое Интегрируйте и выведите уравнение следующей кривой (распределение температуры: Л, , dt 1 1 f g y 1 g 3 1 0 = ’-^ =-^-АР. Hrbd-tb—tb -] — температурный профиль Он остается неизменным в любом положении x. Коэффициент теплопередачи определяется градиентом температуры вблизи стенки. Для критерия нуссельта, основанного на локальной разности между Температура стенки и объемная температура жидкости^, расчет будет следующим: nud = 4. 36. 。 (7-31) в случае постоянной температуры стенки приведенное выше уравнение.
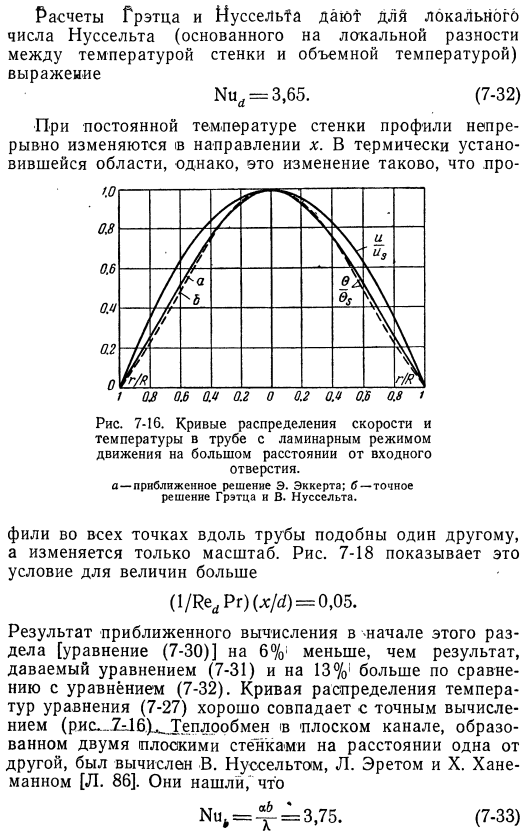
Разделение переменных, когда предполагается, что температура выражается как произведение функции, зависящей только от радиуса, и другой функции, зависящей только от осевого положения. Мы обнаружили, что разность температур 0 уменьшается в осевом направлении, как и в функции e. Радиальные колебания температуры описываются функцией Бесселя. Температура Наклон поверхности трубы снова определяет критерий нуссельта. Расчеты Граца и Нуссельта дают локальные числа нуссельта (основанные на локальных различиях между температурами) Температура стенки и объема) формула nud = 3, 65. (7-32) при постоянной температуре стенки профиль непрерывно изменяет направление ib.
Устойчивое состояние, но это изменение составляет 7-16. Кривая распределения скорости и температуры в трубе со стратифицированной кинетической областью на расстоянии от Вход. A-e. Приближенное решение Эккерта. B-graetz и w. Точное решение Нуссельта. Фили всех точек вдоль трубы похожи друг на друга, меняется только масштаб. Фигура 7-18 показывает это состояние для величин, превышающих (l / redpr) (x / rf) = 0, 05. Результат первого приближенного расчета в этом разделе[формула (7-30) ] составляет 6%! Меньше результатов Формула (7-31) и дается при 13%! Уравнение (7-32) или более.
- Кривая распределения температуры в Формуле (7-27) хорошо согласуется с точным расчетом .(Рисунок 7 = 16) ^ an-теплопередача плоского канала, образованного 2 плоскими стенками на расстоянии друг от друга, v. nusselt, l. Eret и x. hanemann [l. 86]они являются Его 3. 75 было найдено. (7-33) большинство существующих экспериментальных данных по теплопередаче в ламинарном потоке не очень подходят для сравнения с приведенной выше формулой по 3 причинам. Первоначально эксперименты в основном проводились с использованием вязких жидкостей, так как на практике эти жидкости обычно используются в теплообменниках.
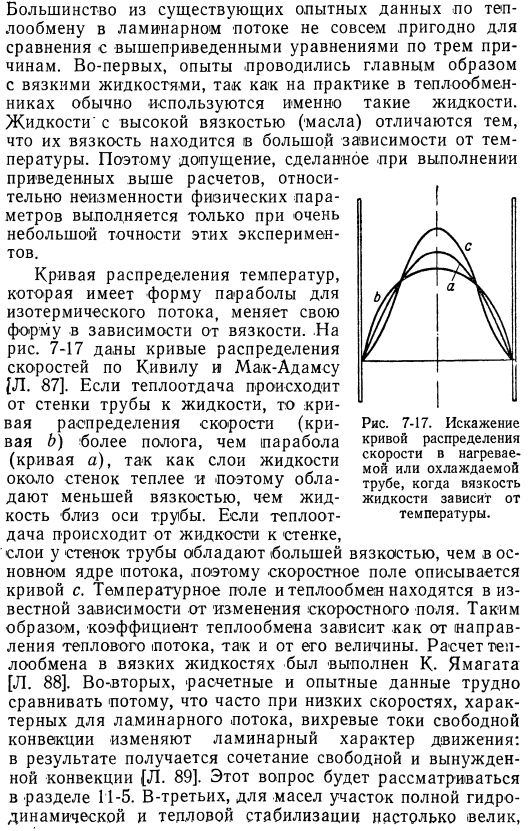
Высоковязкие жидкости (масла) Он отличается тем, что вязкость во многом зависит от температуры. Поэтому допущения, сделанные при выполнении приведенных выше расчетов о неизменности Физические параметры выполняются только с очень малой точностью этих экспериментов. Кривая распределения температуры в виде параболы изотермического течения、 Форма изменяется в зависимости от вязкости. На рис. 7-17 показана кривая распределения скоростей qeeville и mcadams{l. 87. Когда происходит передача тепла от стенки трубы к жидкости、 Кривая распределения скоростей (кривая b) более пологая, чем парабола (кривая a). Это связано с тем, что слой жидкости у стенки теплее и имеет меньшую вязкость, чем жидкость у оси.
Поле скорости представлено кривой c, потому что оно более вязкое, чем основное ядро потока. Людмила Фирмаль
Труба. Если передача тепла от жидкости к стене происходит, то слой стены трубы будет большле than7-17. Искажение кривой распределения скоростей нагретой или охлажденной трубы、 Когда вязкость жидкости зависит от температуры. Температурное поле и теплопередача Известна зависимость от изменения скорости движения field. So, коэффициент теплопередачи зависит как от направления теплового потока, так и от его величины. Расчет теплопередачи в Вязкой жидкостью является К. Ямагата [l. 88]. Во-вторых, трудно сравнивать расчетные данные с экспериментальными данными.
Это часто характерно для ламинарного течения на малых скоростях、 Вихревые токи в свободной конвекции изменяют ламинарную природу motion. As в результате получается комбинация свободной и принудительной конвекции (л. 89]. Проблема в том, что、 Раздел 11-5. В-третьих, в случае масла область полной гидродинамической и термической стабилизации настолько велика, что на практике в теплообменнике возникает»идеально стабилизированный поток». 、 Такое бывает.
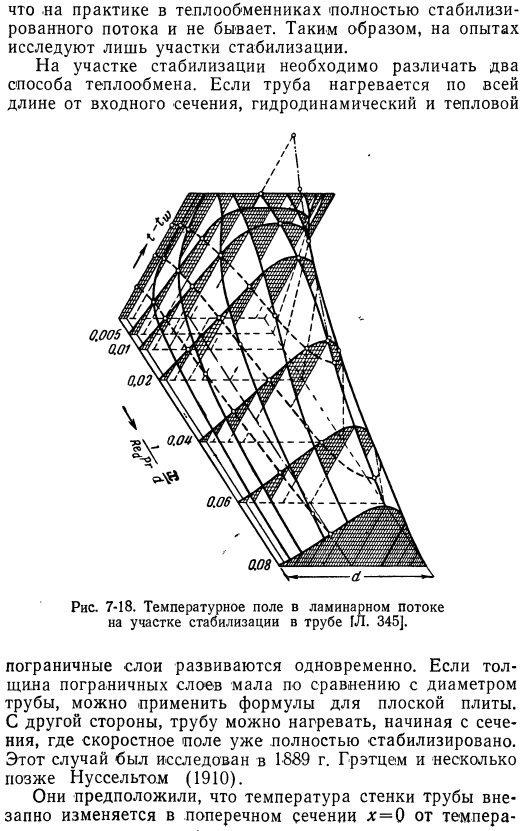
Поэтому в эксперименте используется только участок стабилизации studied. In в разделе стабилизации необходимо различать 2 способа теплообмена. Если труба нагревается по всей ее длине Входное сечение, гидродинамика и тепло 7-18. Ламинарное температурное поле в секции стабилизации трубы 1l. 345]. Пограничный слой развивается одновременно. Если толщина пограничного слоя мала по сравнению с диаметром трубы, можно применить формулу к плоской пластине. С другой стороны, трубы можно нагреть от: Поле уже совершенно стабильно. Этот случай был исследован Гретцем в 1889 году и чуть позже Нуссельтом (1910). Говорят, что температура стенки трубы резко упала Площадь поперечного сечения x = 0 изменяется от температуры, равной температуре поступающей жидкости, до другой постоянной температуры ниже по потоку от x = 0.
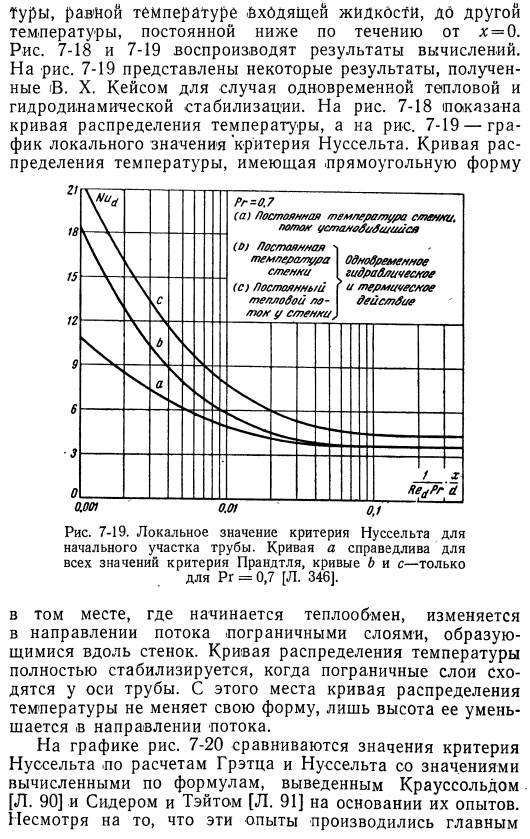
Размножение 7-18 и 7-19 Результат расчета. На рис. 7-19, v показаны результаты, полученные x. key в случае одновременной термической и гидродинамической стабилизации. Рисунок 7-18 (дисплей Кривая распределения температуры и рисунок 7-19 представляют собой график локальных значений критерия нуссельта. Прямоугольная кривая распределения температуры. 7-19. Местный Значение критерия Нуссельта первого участка трубы. Кривая a справедлива для всех значений критерия Прандтля. Кривые b и c равны pr = 0, 7 [l. 346]. Куда? Начинается теплообмен, и направление потока изменяется в зависимости от пограничного слоя, образованного вдоль стенки.
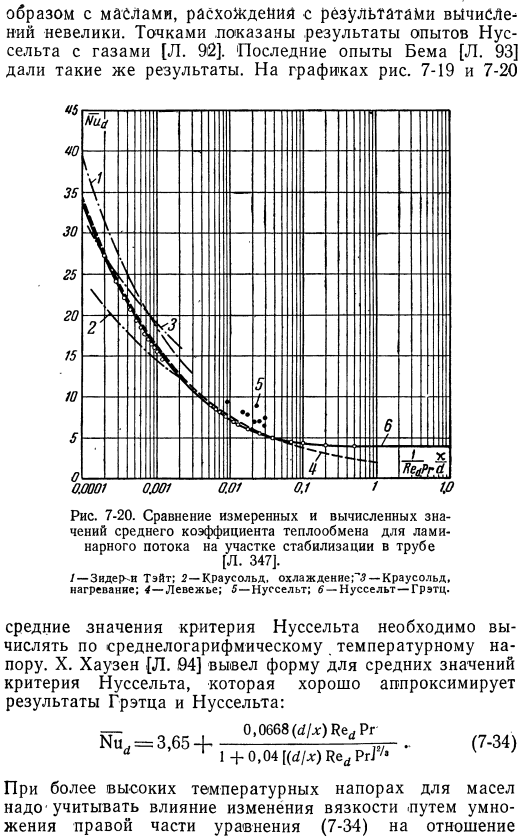
Кривая распределения температуры Слои сходятся на оси трубы. С этого момента форма кривой распределения температуры не изменяется, только высота уменьшается в направлении потока. Диаграмма на рисунке сравнивает между 7 и 20 Значение критерия Нуссельта по расчету Греца и Нуссельта, Крауссольда [l. 90]и сидера и Тейта [l. 91] основано на их опыте. Несмотря на то, что эти эксперименты проводились в основном на нефти, есть небольшое расхождение с результатами расчетов. Dot показывает результаты экспериментов nuselt с использованием газа[l. 92]. «Недавний эксперимент Бема [l. 93]дал то же самое result. In на схеме графики 7-19 и 7-20 7-20.
Сравнение измеренных и рассчитанных средних коэффициентов теплопередачи Ламинарное течение в стабилизационном сечении трубы[l. 347]. 1-сторона[> n Тейт; 2-краусольд, охлаждение;^ -? — Краусольд, отопление; 4-Левье; 5-нуссельт; 6-нуссельт-Гретч. Среднее значение критерия Нуссельта следует вычислять по среднему логарифмическому значению температуры напора. Х. Хаузен. 94] мы получили форму среднего значения критерия Нуссельта. Результаты graetz и nusselt хорошо аппроксимированы: 0. 0668 (tz / x) red pg 1 4-0. 04 [ (d [x) red pgg / v при высокой температуре давления в масле, эффект изменения Формула (7-34) отношение на правой стороне (Нв / jiu’⁰), умножив 1⁴, tsv является вязкостью при объемной температуре или средней температуре интегрирования жидкости, p. W является Температура стенки трубы.
Физические параметры берутся при объемной температуре жидкости. Для газов, целесообразно использовать формулу (7-34) без добавления коэффициента вязкости. Как показано в Формуле (7-16), характеристики должны быть введены при относительном temperatures. In литература, сведения о теплопередаче ламинарного потока в трубах входной области Часто называемый числом Граца, он отображается как функция безразмерного параметра, который является обратным параметру, используемому в качестве абсциссы диаграммы. 7-19. И 7-20. An статья была опубликована Норрисом и Стрейдом, который суммирует соображения различных температурных условий вдоль стенки трубы. [Л. 95].
Некоторые характерные особенности Свойственна теплопередача, связанная с ламинарным течением через каналы некруглого сечения. Этот случай был изучен аналитически. 96] стабильное тепло и Гидродинамический поток через канал, поперечное сечение которого имеет веерообразную форму, в условиях, когда тепловой поток от стенки канала к жидкости постоянен в направлении Ось канала. Локальный коэффициент теплопередачи сильно изменяется по всему каналу, в углах он приближается к нулю, а средний коэффициент равен Теплообмен сильно зависит от граничных условий. 2. Рассмотрены два граничных условия по периметру канала. Температура стенки постоянна по периметру и локально Постоянная жара flow. It было установлено, что критерий нуссельта, усредняющий всю окружность при постоянной температуре стенки, в 7 раз превышает значение постоянного теплового потока. Веерообразный угол вершины составлял 20°.
Если угол вершины равен 60°, то отношение этих 2 чисел нуссельта равно 2, 5. Коэффициент теплопередачи числа нуссельта определяется как ocpeji Тепловой поток qw делится на разность между объемной температурой жидкости и средней температурой стенки (усредненной по всему периметру канала). Приведенные выше результаты Это показывает, что необходимо тщательно задавать соответствующие граничные условия, используя общедоступные данные о коэффициенте теплопередачи. .I ЗАДАЧИ 7-1 выведено интегрируемое уравнение энергии пограничного слоя для стационарного осесимметричного течения вокруг цилиндра, ось которого параллельна направлению flow .To предположим Физические свойства изменяются в зависимости от давления и температуры .
Определите величину конвекции в этих условиях .7-2 .Обобщить интегрируемое уравнение энергии пограничного слоя Быстрый поток путем включения элементов, которые описывают тепло, производимое трением .7-3 .Вычислить толщину теплового пограничного слоя стационарного 2D ламинарного потока Если температура поверхности передней кромки пластины равна температуре потока жидкости, а температура поверхности увеличивается линейно, то она течет по круговой пластине Направление потока .Используйте уравнения пограничного слоя, которые могут быть интегрированы .Повторите расчеты в разделе 7-3 и посмотрите, какие изменения необходимо внести, чтобы учесть .разница температур изменяется вдоль х .7-4 .
Вычислите локальное значение критерия Нуссельта для условий, описанных в предыдущей задаче, но используйте метод, описанный в разделе 7-4 .Интегралы, отображаемые в вычислении, могут быть преобразованы в табличную гамма-функцию .7-5 .Докажите, что форма кривой распределения скорости идентична кривой Число ПР-1 ламинарное распределение температуры с постоянной скоростью на плоской пластине .7-6 .Выведите уравнение (7-25) теплообмена в потоке Переменная f, v’, m вводится в уравнение энергии бесконечного клина / пограничного слоя .7-7 .Жидкое масло с характеристиками, указанными в таблице в приложении .П-3 измельчитель При скорости 13, 5 м длина латунной трубки 3 м (а, 12, 7 мм) {мин, охлаждается от 93 до 38°с .Температура внутренней поверхности трубы составляет 27°С .
Внутренний мир .7-8 .Рассчитайте кривую распределения температуры для гидро — и теплостойких ламинарных течений по круглым трубам Поперечное сечение при постоянном течении через стенку трубы и постоянной температуре стенки .При расчете примите, что скорость является постоянной в поперечном сечении pipe .To вычислить Критерии нуссельта для обоих граничных условий .Полученные результаты в дальнейшем показали хорошую аппроксимацию устойчивого турбулентного теплообмена Жидкостная труба с очень малыми значениями теста Прандтля .7-9 .Выполните тот же расчет, что и в предыдущей задаче для канала, образованного 2 плоскопараллельными Пластина .
7-10 .Рассчитайте коэффициент теплопередачи и значения критерия Нуссельта для термически и гидравлически стабилизированного ламинарного течения через сформированный канал 2 параллельные пластины при следующих граничных условиях: а) система 1 поддерживается от 1 до заданной температуры .Например, (Л .см .[97] .Температура жидкости, другие стены изолированы . b) обе стены поддерживаются при 2 различных постоянных температурах . в) Удельный тепловой поток передается от 1 Стена к жидкости, другая стена, которую нужно изолировать .
Смотрите также:
| Поперечное омывание цилиндрических тел | Аналогия между количеством движения и теплообменом |
| Точные решения уравнения энергии ламинарного пограничного слоя | Движение жидкости в трубе |

