Оглавление:








Движение жидкости в трубе
- Расчет расхода в трубе вблизи входа также может быть выполнен с использованием уравнения импульса (6-8). Для труб круглого сечения выведено уравнение импульса^и l решается для несимметричного течения. И. М’» И — — — — — — ИС —— Рисунок 6-18. Развитие полей скоростей при ламинарном движении внутри трубы стабилизирующего узла. Этот расчет основан на соотношении л. Шиллера [l. 56]. Он создал кривую распределения скорости из 2 парабол, Соединенных прямой линией.
Верхняя часть ветвей каждой параболы находится на границе пограничного слоя (рис. 6-18). Скорость основного ядра потока вне пограничного слоя Такое же количество жидкости проходит через любой участок трубы, который увеличивается в направлении движения жидкости и увеличивает толщину пограничного слоя. Следовательно, согласно уравнению Бернулли справедливо. Центр подачи, давление drop. At конец участка стабилизации (расстояние от входа), кривая распределения скоростей поперечного сечения имеет форму параболы.
На микроскопическом уровне эта работа осуществляется силами, действующими между молекулами на границе контакта более нагретого тела с менее нагретым. Людмила Фирмаль
«Разница в давлении между поперечным сечением с гидравлически стабилизированным потоком и областью вне трубы, где скорость потока незначительна, может быть определена путем приложения потери давления к потере давления, которая возникает, когда поток стабилен по всей длине трубы. ДП = 2. 16p4 -. (6-47) Результаты этого расчета согласуются с экспериментальными данными. Отношение длины стабилизирующего участка к диаметру трубы является функцией критерия Рейнольдса. = 0. 0288 ^ = 0. 0288 красный. — Л (6-48) Критерий Рейнольдса рассчитывается по средней скорости конкретного участка и диаметру d трубы. Именно так в технической литературе обычно рассчитывается критерий Рейнольдса.
Однако следует иметь в виду, что на практике невозможно провести резкую границу между участком стабилизации и гидравлически стабилизированной зоной течения. Поток асимптотически приближается к требованию гидравлической стабилизации. Таким образом, на расстоянии, превышающем по формуле lₑy (6-48) длину участка стабилизации, можно обнаружить отклонения от полностью стабилизированного режима. Если значение критерия Рейнольдса превышает критический критерий, то где-то на участке стабилизации режим движения пограничного слоя изменяется на turbulence. As опорное значение Рейнольдса увеличивается, переходная зона приближается к входу.
Поскольку толщина турбулентного пограничного слоя увеличивается быстрее, чем ламинарного течения, длина стабилизирующего участка сокращается по[эталонной формуле (6-35) ]. В pub-3000 весь поток в области стабилизации является по существу ламинарным、 В этом случае приблизительно 100cf равно[справочная формула (6-48) ]. Если значение критерия Рейнольдса увеличить сверх этого значения, то длина участка стабилизации сначала быстро уменьшится примерно до 40d, а затем снова начнет увеличиваться. Установившийся ламинарный поток через кольцевую трубу равен 1 во многих случаях, когда получено простое и точное решение уравнения Навье-Стокса.
Это решение показывает, что профиль скорости является параболой и дает коэффициент трения по формуле (6-53). 。 ⁶-⁴⁹) Этот тип потока обычно называют потоком пуазейля. Кривая распределения скоростей в области гидродинамически стабилизированного течения re = 0, 00000 хорошо объясняется в° ° rmul°6 (6-32), если толщина пограничного слоя заменяется радиусом r. Это соответствует предположению, что пограничный слой замыкается вдоль оси pipe. In в этом случае uₛ обозначает скорость движения вдоль оси. Справедливы также уравнение для определения напряжения трения на поверхности пластины (6-33) и уравнение для определения кинетической скорости на границе между турбулентным пограничным слоем и ламинарным подслоем (6-36).
Последние формируются в трубе таким же образом, как и поверхность пластины. Если в приведенном выше уравнении радиус r заменяется диаметром d, а скорость и$являются средней скоростью wₘ, то по Интегралу формулы (6-32) находим, что uₘ=0. 82 fzₛ. Это будет использовано позже. На самом деле здесь, как и в случае с пластинами, нет четкого слоистого слоя, но、 Только постепенно уменьшается турбулентность по мере приближения к стене. Уравнение, учитывающее существование такой переходной зоны, показано на рисунке. 6-20. Коэффициент трения определяется по формуле/, а не по напряжению трения/ ^ = / 44 ’ ⁶ — ⁵3) /- Зет. * 2. Рисунок 6-19. Применение закона импульса к гидродинамически стабильному течению в трубе.
Где dp-перепад давления в участке трубы l. По закону импульса между давлением в участке 1-1 и напряжением трения в стенке участка трубы длиной l 2-2 (рис. 6-19) В устойчивом потоке существует равновесие. Поэтому стабильно. То. .(6-54) Коэффициент трения можно рассчитать по напряжению трения, используя формулы (6-50), (6-53) и (6-54) .(6-55) Это выражение эго обычно называют законом brazius .Если движение жидкости связано с теплопередачей, то возникает определенный температурный напор .Согласно McAdams, физические параметры газа[L .57] — это температура (Z ^ — f — / m) / 2 (tw-температура стенки, tₘ-средняя температура потока), а Sider и Tate [L .[58], коэффициент трения масла рассчитывается путем умножения (Hm / Pb⁰), 1⁴ » на физические параметры, полученные при температуре tₘ .
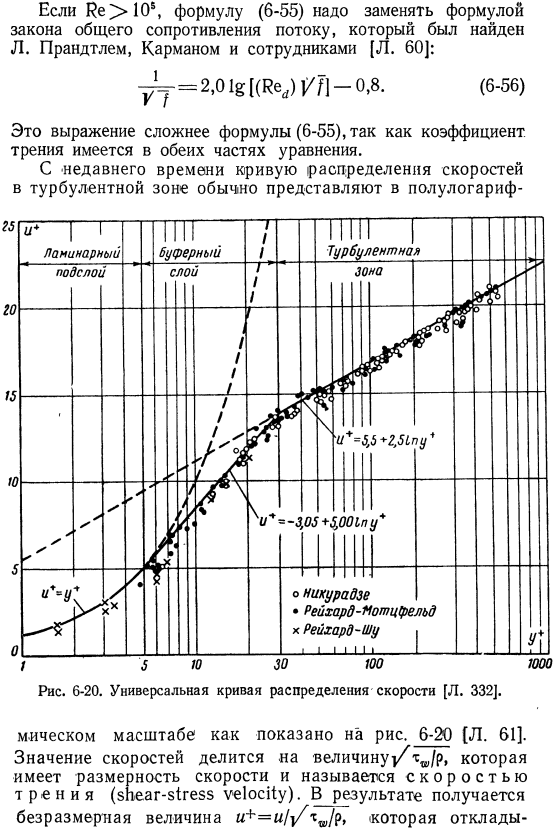
Где pt-вязкость tₘ, а t-вязкость tw .Экспериментальные данные Rohonczy[L .59]если физический параметр получен при температуре t’i, то вода наилучшим образом подходит к результату расчета по формуле (6-55) Для Re> 10s формула (6-55) должна быть заменена формулой закона общего сопротивления потоку, открытого Прандтлем, карманом и коллегами[L .60 .]: г = — = 2 .01 г [ (Красный) ///] −0 .8 (6-56) Поскольку коэффициент трения существует по обе стороны уравнения, эта формула является более сложной, чем формула (6-55) .В последнее время кривая распределения скоростей для зон турбулентности обычно выражается как полу-логарифм Рис .6-20 .Универсальная кривая распределения скорости[L .332] .В то же время, как показано на фиг .6-20 [л . 61] .
Скорость величина делится на величину^ / технические / С .Он имеет размерность скорости и называется скоростью касательного напряжения .В результате, мы получим безразмерную величину#+=#/) / технические / Р7 .Он отображается на вертикальной оси .Расстояние от стенки трубы преобразуется в критерий Рейнольдса путем умножения скорости трения и деления на коэффициент кинематической вязкости: y + = y это осадочное значение- Горизонтальная ось .Поэтому в данном случае кривая распределения скоростей не является функцией критерия Рейнольдса, поэтому ее называют универсальным распределением скоростей curve .In на графике рисунка 6-20 показаны результаты экспериментов с Никурадзе, Рейхардтом и др .
- Вместо линейной зависимости полулогарифмического масштаба между скоростью и расстоянием от стенок области ламинарного подслоя существует. Другая функциональная зависимость на левой стороне графика, которая представлена в виде curve .As вы можете видеть из графика, что данные эксперимента соответствуют этой кривой примерно в g / ⁺ = 5 .Прямая линия справа показывает поле скоростей в турбулентном ядре потока .На графике видно, что между ламинарными подслоями и турбулентным ядром существует буферная зона, и турбулентность постепенно исчезает в направлении wall .To описав поле скоростей в буферной зоне, Калман [л . 62]предлагает отрезок прямой линии и отображает его на графике, а также устанавливает границу этой зоны-5 И£ / ⁺2= −30 .
На рисунке показана формула для всех 3-х участков кривой распределения скоростей .6-20 .— Эти формулы справедливы и для труб с шероховатыми стенками, но необходимо вводить новые параметры, отражающие степень шероховатости[л . 63] .При изучении влияния шероховатости поверхности возникают некоторые трудности из-за того, что до сих пор нет удовлетворительного геометрического описания шероховатой поверхности с ограниченным числом parameters .It общепринято, что наиболее важным параметром является отношение средней высоты бугорков к диаметру pipe .In своими многочисленными экспериментами по трению трубы с шероховатой поверхностью Никурадзе воссоздал образец определенной шероховатости путем наклеивания на поверхность трубы достаточно однородного размера песка и создания максимально плотного покрытия .
Фактически при теплообмене энергия передаётся посредством электромагнитного взаимодействия при столкновениях молекул. Людмила Фирмаль
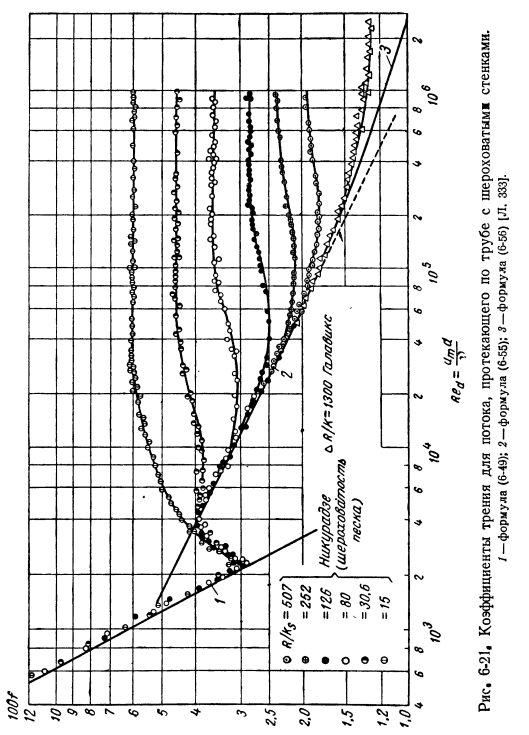
Значение коэффициента трения, определенного таким образом, показано на рисунке .На рис .6-21 красные значения нанесены по абсциссе и соотношению R / kₐ Рисунок 6-21 .Стена пропускает через грубую трубу коэффициент трения потока . / — Формула (6-49) ; 2-Формула (6-55) ; 3-Формула (6-56) [L .333] .Является параметром (k-средняя высота отбойника, R-радиус трубы) .Очевидно, что шероховатость не влияет на трение как в ламинарном, так и в малом числе Рейнольдса turbulence .In этот участок стенки трубы считается «гидравлическим и гладким« .Это связано с тем, что все бугорки целиком лежат на слоистом подслое .
Если число Рейнольдса достаточно велико, то кривая коэффициента трения принимает горизонтальное направление, что свидетельствует о том, что падение давления в этом диапазоне возрастает пропорционально мощности 2 среднего velocity .In эта область, локальное отверстие элемента шероховатости в основном способствует падению давления .Исследования шероховатости других форм показали, что форма кривой коэффициента трения часто отличается от кривой, показанной на рисунке .6-21 .Измерения производятся на трубе с шероховатой поверхностью, которая фактически используется, Moodi [L .64] .
Результаты этих измерений свидетельствуют о постепенном снижении коэффициента трения таких поверхностей до определенного значения (критерий Рейнольдса повышен, и нет явных отклонений в кривых рисунков 6-21) .Кривые на рис .6-21 соответствуют измерениям Galix .Поверхность находилась в хорошем согласии с коэффициентом трения грубой трубы и измерением профиля скорости .Этот материал может быть использован в виде глины .Шлихтинг [Л .65]подробно описано в книге .
Когда толщина пограничного слоя равна радиусу трубы, в качестве первого приближения можно использовать данные на рис .6-21 для получения коэффициента трения пластин с шероховатой поверхностью .Трубы, используемые в этой технике, часто имеют небольшую форму поперечного сечения .Коэффициент трения установившегося ламинарного потока через трубу некруглого сечения является выражением той же формы, что и Формула (6-49), но в этом случае величина численной постоянной зависит от формы сечения section .In случай труб такого сечения, как линейные размеры, входит в критерий Рейнольдса, так называемый «эквивалентный диаметр», который определяется по формуле」 」 (6-57) Где а-площадь, а c-периметр поперечного сечения .
Для канала medudu с 2 плоскими параллельными пластинами гидравлический диаметр равен 2 расстояниям между стенками .Если в формулах (6-49) и (6-53) вместо d используется гидравлический диаметр, то численная константа формулы (6-49) имеет значение 96 для этой площади поперечного сечения .Установившийся турбулентный поток через некруглую трубу (канал), уравнения (6-55) и (6-56) заменяются эквивалентными по диаметру этими уравнениями и уравнениями (6-53), которые показали, что диаметр, определяющий коэффициент трения, описывает коэффициент трения с достаточной точностью) .
Это положение эффективно, если в поперечном сечении отсутствуют острые углы .Числовые константы не изменяются .Представляют интерес наблюдения за процессом перехода от ламинарного течения к турбулентному в канале с полигональным сечением .Переход в этом случае осуществляется не при определенном значении критерия Рейнольдса, а в диапазоне Рейнольдса numbers .In кроме того, с увеличением числа Рейнольдса поток изначально становится турбулентным в центре жидкости, но остается ламинарным в области угла .С увеличением нормы Рейнольдса, турбулентность постепенно проникает в углы .. * Поведение этого потока наиболее ощущается под небольшим углом. Это подтверждается наблюдением за потоком и измерением профиля скорости [l. 66].
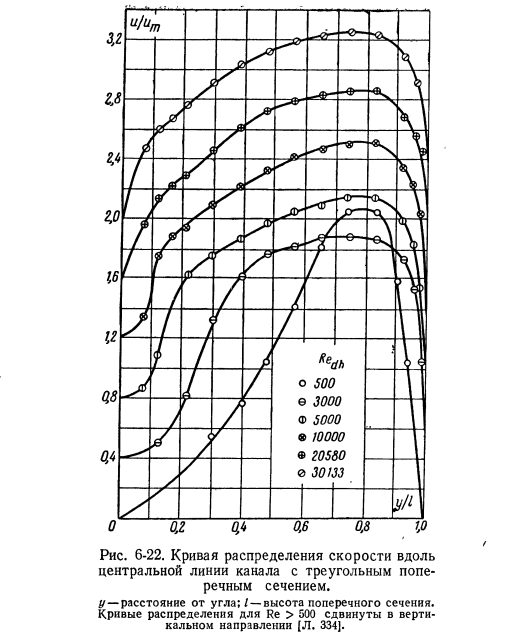
На рис. 6-22 показан такой профиль, измеренный по высоте треугольного сечения канала. Поперечное сечение канала представляло собой равнобедренный треугольник, в котором отношение высоты l к основанию было равно 5. Для эталонного Красного Рейнольдса / i = 500 поток является полностью ламинарным, а кривая распределения скорости имеет пикообразную форму, которая увеличивается параболически вблизи небольшого угла. Красный Нет.
При 3000 пик кривой распределения становится более плоским, но параболическое увеличение скорости продолжает превышать примерно половину высоты, что указывает на то, что поток в этом диапазоне вокруг малого угла по-прежнему является существенно ламинарным. Только в случае красного№= 20 580 турбулентный поток распространяется по всей площади поперечного сечения. Рисунок 6-22. Кривая распределения скоростей вдоль осевой линии канала с треугольным сечением. Y-расстояние от угла. Я-Высота поперечного сечения. Кривая распределения re> 500 смещается в вертикальном направлении (л. 334].
Смотрите также:
| Градиенты давления вдоль поверхности | Поперечное обтекание цилиндра |
| Точные решения уравнении ламинарного пограничного слоя для плоской пластины | Обтекание осесимметричных тел |

