Оглавление:





Движение тяжелой точки в пустоте
- Для начала координат получите начальное положение точки. ось Y направлена вертикально вверх, а ось X направлена горизонтально в плоскости траектории. Уравнение движения. Начальная скорость u0 и угол, образованный осью Ox, получены из первого уравнения =потому что в версии v0 Х = в Т потому что. Второе уравнение также быстро интегрируется и выглядит так: Да. dt ГТ + v0 в грех 1 2 1 2 3 Т з В = А + в v0 А. грех Формулы 1 и G определяют скорость. V2 = V2 COS2 a 4 v0 sin a gt 2 = vj 2 y. Численное значение скорости в каждой точке берется из положения вертикальной скорости Vq 2, как если бы точка упала без начальной скорости. Уравнение 3 выводится непосредственно из теоремы о кинетической энергии.
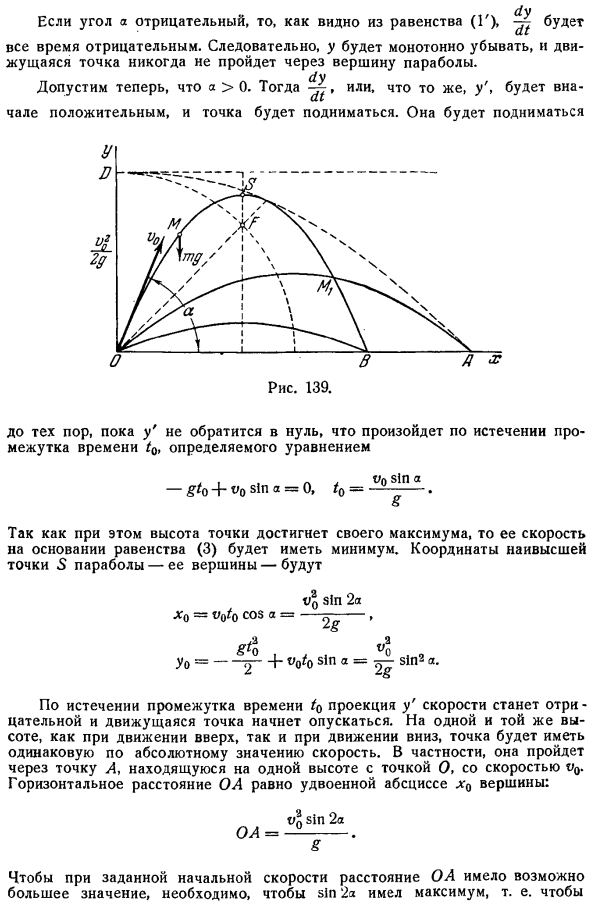
Если убрать t из уравнений 2 и 2, то получится орбитальное уравнение. В Эго парабола с вертикальной осью, обращенной вниз рис. 139.Если угол a отрицателен, как видно из равенства D , то всегда будет negative. As в результате y монотонно уменьшается, и точка движения не проходит через вершину параболы. ды Теперь предположим, что это a 0.Тогда, или в то же время, y сначала будет положительным, и точки будут расти.
Если точка находится в равновесии, то сила будет нормальна к поверхности и, следовательно, ко всем возможным перемещениям. Людмила Фирмаль
Она поднимется это происходит после интервала времени 0, определенного выражением, пока y не исчезнет это хорошая вещь. Л. вентиляционно перфузионное грех Джио + вентиляционно перфузионное грех= 0 0 = О В этом случае высота точек достигнет максимума, поэтому скорость, основанная на равенстве 3, будет минимальной. Координаты высшей точки параболы ее вершин это Вентиляционно перфузионное грех 2а Хо vofo потому что = —— Йоу = 2 + О О С Н А = 2 СЛН По мере прохождения времени Iq проекция скорости y становится отрицательной, и точка движения начинает fall. At на одной и той же высоте, как при подъеме, так и при спуске, абсолютная скорость точек будет равна same.
В частности, он проходит через точку А, которая находится на той же высоте, что и точка О со скоростью v0.Горизонтальное расстояние ОА равно 2 раза абсциссы л0 вершины. Грех 2а Чтобы расстояние ОА было как можно большим при заданной начальной скорости, sin 2a должен быть максимальным, то есть угол a должен быть равен 45.Предположим, вы хотите достичь точки Два V6 Абсцисса есть меньше чем. Наклон съемки определяется по формуле sin 2a = OB. Это указывает на то, что существует 45 различных 2 solutions. So вы можете достичь 2 параболы в точке B. In за более короткое время легко заметить, что точка попадает в цель B вдоль нижней параболы.
Положение параболы, соответствующее заданному углу а, может быть определено геометрически. Заметим, что для этой цели все параболы, полученные изменением угла a, имеют общую прямую линию, линию D с ординатой Vq и 2. фактически параметры параболы, описываемой движущейся точкой, являются Прямое уравнение имеет вид Итак, это линия D, которая расположена на высоте, до которой можно добраться, если точка движения подброшена вертикально вверх со скоростью u0. Этот результат становится очевидным, когда вы начинаете с уравнения 3. c , это уравнение имеет вид Эта линия прямая, потому что она будет в воображаемой точке пересечения траектории и линии y = y it Парабола.
- Теперь, когда мы установили это, предположим, что нам дана касательная к траектории в начале координат. И фокус F является прямой линией такой, что прямая линия Oo0 является биссектрисой угла FOD. In кроме того, он расположен на окружности с радиусом OD, которая описывается из точки O, как из center. So он находится на пересечении этого круга и линии. Эта структура указывает на то, что геометрическим локусом фокуса параболы является окружность, центрированная в точке O радиуса OB. Чтобы попасть в определенную точку плоскости xx, yt , ставится задача нахождения угла, под которым необходимо выпустить снаряд.
Вводя обозначение tan a = u и подставляя заданную точку M1 в уравнения локуса координат x, y, получаем уравнение 2 го порядка для определения, так как локус должен проходить через эту точку. Y1 = TT 1 + 2 + ih1 2v0 Условием важности корня является формула 1 3 Для его геометрической интерпретации рассмотрим параболу с уравнениями 2 2 Два Эта парабола имеет вершину в параметрах VJ g и x = 0, y= , то есть D , поэтому акцент делается на начало координат. Условия значимости 2 означают, что точка должна находиться внутри или выше этой параболы безопасная парабола.
Необходимые и достаточные условия равновесия системы заключаются в том, что для любого возможного ее перемещения, допускаемого связями, сумма возможных работ непосредственно приложенных сил равна нулю. Людмила Фирмаль
Если точка находится внутри безопасной параболы, то уравнение имеет 2 различных действительных корня, и 2 различными способами оно может достичь точки Afj и выстрелить снарядом под 2 различными углами рис.139.Если точка L1G находится на безопасной параболе, то корни уравнения имеют 2 перекрытия и могут достигать точки Afx только 1 способом. И если в уравнении есть 2 разных корня, то есть 2 орбиты, проходящие через Mlt, соответствующие значениям 2 aj и угла A. время, необходимое для достижения точки Afx вдоль обеих траекторий, равно Х Х ч 1 — Потому что по качеству звука в 04 версии v0 со А1 Короткое время соответствует меньшему из углов a и a.
Парабола безопасности достаточна для представления этого уравнения, чтобы дождаться огибающей траектории, возникающей в результате изменения угла a, т. е. огибающей кривой, которая обозначается уравнением 1, где величина и a являются переменными параметрами. Но это именно то, что мы сделали, чтобы найти безопасную параболу. Эти результаты легко получить даже геометрически рис. 140. Необходимо пройти через 2 точки и создать параболу с определенным direction.
Мы видели, что его фокус находится на круге с радиусом OD, сосредоточенным на точке O. It он также должен находиться на окружности, центрированной на корме, где должна проходить парабола. Эти 2 окружности могут пересекаться в 2 точках F и F .Таким образом, может быть 2 parabolas. To сделайте так, чтобы эти круги пересекались, не делайте этого Расстояние между центрами OM должно быть меньше суммы и больше разности радиусов. SL их OQ, и поскольку OQ это разница в радиусе, последнее условие явно выполняется. Поэтому достаточно написать На самом деле OAfx ОД пом. нарисуйте линию D на расстоянии 2 OD от оси x и продолжайте с MXR до пересечения этой линии и с.
Затем условия, которые должны быть выполнены, принимают следующий вид: A 0 Afx 7.Но геометрическое место точке,= М это параболы направлены на происхождение и D. направление это будет парабола. Если точка находится внутри этой параболы, вы можете попасть в нее двумя способами. Если он находится на параболе, есть только 1 орбита, проходящая через это point. In такая точка, фокус орбиты и фокус безопасной параболы находятся на прямой линии с точкой Mr. базовая структура, определяющая касательную в точке Afp, указывает, что эта касательная одинакова для обеих парабол.
Смотрите также:
Решение задач по теоретической механике

