Оглавление:




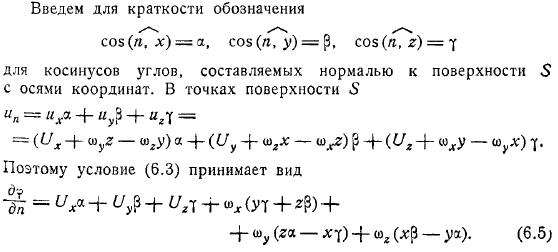



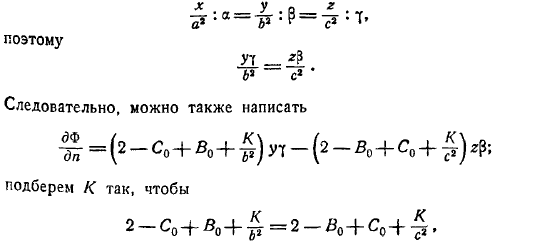
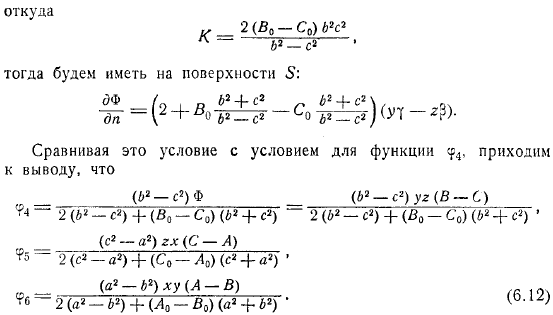

Движение твердого тела в безграничной жидкости
Движение твердых тел в неограниченной жидкости. Рассмотрим гидромеханику и движение жидкости, вызванное движением объекта, окруженного поверхностью, с бесконечной, несжимаемой идеальной жидкостью, которая бесконечно. В этом случае предполагается, что нет никакой внешней силы, действующей на жидкость, и нет никакого вихря в движении жидкости.
Для представления осесимметричных тел рассматриваемого мгновенного потенциала скорости по проекция скорости равна. Уравнение неразрывности указывает, что функция должна удовлетворять уравнению Лапласа по всей области течения, то есть вне поверхности. Подумайте о возможности как уникальный. В каждой точке на поверхности должны быть выполнены граничные условия.
- Где скорость имеет проекцию на точку той же поверхности, что и нормаль к поверхности.
- Для ясности предположим, что нормаль находится вне поверхности, то есть внутри жидкости.
- Условие, что жидкость бесконечно стационарна, приводит к граничному условию. Можно предположить, что мы стремимся к нулю при одинаковой величине.
Фактически, сферическая координата вводится вокруг начала координат, и она постепенно расширяется в окрестности ряда бесконечных точек. Людмила Фирмаль
Отбрасывание некритических констант имеет следующую форму разложения. Сферическая функция. Предположим, у вас есть сфера с радиусом, центрированным в начале координат.
Из-за несжимаемости жидкости скорость потока через нее должна быть равна нулю. И с тех пор для того чтобы определить функцию, необходимо знать величину, то есть составляющую скорости точек этой поверхности перпендикулярно поверхности. Но известно для гидродинамических реакций при движении тела, что распределение скорости твердого тела полностью определяется установкой скорости точки этого объекта и установкой угловой скорости вращения объекта.
- Выбираем начало координат этой точки, которое обозначается вектором скорости этой точки (которая считается неподвижной связью с телом), и через вектор угловой скорости вращения тела, для скорости тела и любой точки, получаем формулу.
- Итак, вблизи точки бесконечности происходит разложение формы: вот радиус-вектор точки относительно точки. В проекции на координатные оси это выглядит так.
Для простоты косинус угла складывается из нормалей поверхности с осями. Точка поверхности. Поэтому условие принимает следующий вид. Эта функция указывает, что она должна отображаться в следующем формате. Кроме того, все функции должны удовлетворять уравнениям и условиям.
На поверхности эти функции должны соответствовать условиям. С тех пор условия были четко соблюдены. Людмила Фирмаль
Поскольку условия больше не зависят от векторов, все функций определяются выбором формы поверхности и системы координат. Если сравнить условие с общим условием, то можно увидеть, что функция соответствует случаю движения тела в следующих случаях. То есть, когда тело движется параллельно оси с единичной скоростью. Функции имеют аналогичное значение.
Аналогично функция соответствует следующему случаю То есть, если тело вращается вокруг оси с угловой скоростью вращения, равной. Например, определите эти функции, когда тело является трехосным эллипсоидом. Найдено решение задачи о потоках, обтекающих эллипсоид, бесконечная скорость которого параллельна положительной оси. Если вы возьмете формулу, вы получите решение.
Накладывая на поток, представленный этим решением, поток. Получить потенциал скорости в ответ на равномерное движение параллельно оси со скоростью, равной единице Скорость в бесконечно неподвижной жидкости соответствует движению эллипсоида, параллельного оси. Точно так же, это выглядит так.
Обратите внимание, что на поверхности есть очевидное равенство Эта функция может быть получена из следующих соображений: эта функция удовлетворяет уравнению Лапласа для легкого. Бесконечность, эта функция стремится к нулю как степень. Но на поверхности есть равенство. Для этого. Так что вы также можете написать. Мы выбираем этот путь Откуда? Он появится на поверхности. Если сравнить это условие с условиями функции, то можно сделать вывод.

