Оглавление:



Движение твердого тела параллельно неподвижной плоскости. Общие положения
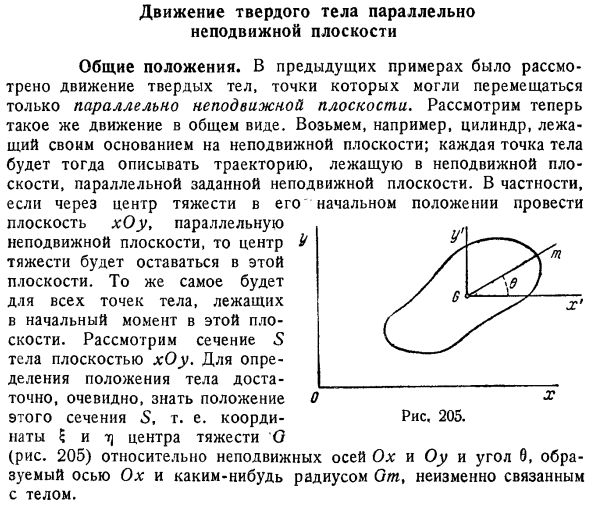
- В предыдущем примере рассматривалось движение твердых тел, точка которого могла перемещаться только параллельно неподвижной плоскости. Теперь рассмотрим те же движения в общем виде. Например, рассмотрим цилиндр, расположенный на нижней поверхности в неподвижной плоскости. Каждая точка в теле представляет собой Локус в неподвижной плоскости, параллельной данной неподвижной плоскости. Особенно если он проходит центр тяжести в исходном положении. Плоскость xOy параллельна неподвижной плоскости, центр тяжести остается в этой плоскости. То же самое относится ко всем точкам тела в первый момент этого плана. Рассмотрим поперечное сечение тела по xOy plane.
To определив положение тела, достаточно знать положение этого участка S, то есть координаты и m центроида G рис. 205 для неподвижных осей Ox и Oy, а также угол 9, образованный осью Ox и определенным радиусом Gmt. It постоянно связан с телом. Предполагая, что на тело действует внешняя сила, проекции на оси Ox и Oy равны XL, Ylt X2,Y2… обозначается Тогда мы сначала создадим 2 уравнения по теореме о движении центроида. Где сумма 2 распространяется на все внешние силы. Нарисуйте оси Ox и Gy через центроид G, параллельный неподвижной оси, и координаты точек тела относительно этих осей равны X , y , а моменты инерции тела перпендикулярны оси gz x gy плоскость Mk2.
Движение твердого тела параллельно неподвижной плоскости. О стремлении материальных систем избегать трения. Людмила Фирмаль
Относительным движением тела относительно оси Gx y z является его вращение с угловой скоростью вокруг оси Gz. Поскольку теорема об угловом моменте может быть применена к движению вокруг оси GZ , мы имеем следующее уравнение: МК = х г г х. Последнее можно получить таким же образом, как и в случае с 359, используя теорему о кинетической энергии при относительном движении вокруг центра тяжести. Это 3 уравнения, которые определяют 5, y, 0 в функции T. из комбинаций этих уравнений, которые могут заменить одно или другое, мы упомянем следующее: 1. уравнение получено путем применения теоремы импульса относительно неподвижной оси Oz, перпендикулярной плоскости xOy.
- Согласно доказанной нами теореме, сумма угловых моментов различных точек тела относительно оси Oz равна величине углового момента массы Л4. Существует комбинированное уравнение массы, которое должно быть сосредоточено в центроиде и моменте импульса L1L2 в относительном движении вокруг оси Gz АО 5 + I= 2 2.Уравнения, полученные путем применения теоремы о кинетической энергии к абсолютному движению. Согласно теореме Кенига 349, кинетическая энергия системы равна Итак, есть уравнение в скобках справа side. dz равен нулю во всех отношениях, поэтому нет 3 го члена.
Когда J проходит через мгновенный центр вращения плоскости диаграммы S, на которой показан момент инерции объекта относительно оси, перпендикулярной плоскости xOy, кинетическая энергия объекта выглядит следующим образом: Тело вращалось вокруг этой мгновенной оси. Однако ось, о которой идет речь, движется в теле, поэтому величина J является переменной. Обратите внимание, что корпус может иметь и другие соединения, помимо тех, которые движутся параллельно неподвижной плоскости xOy. Тогда реакции, порожденные этими связями, должны быть включены в правую часть предыдущего уравнения и исключены из него.
Теорема моментов количеств движения в относительном движении вокруг центра тяжести. Вращение твердого тела вокруг неподвижной оси. Людмила Фирмаль
Однако если эти связи не зависят от времени и выполняются без трения, то реакция связи не включается в уравнение кинетической энергии 5. Если существует несколько тел, движущихся параллельно неподвижной плоскости, то можно применить к каждому из них вышеприведенные уравнения, а затем либо исключить взаимные реакции объектов, либо применить общую теорему к совокупности этих тел.
Смотрите также:
Теоретическая механика — задачи с решением и примерами
Если вам потребуется заказать теоретическую механику вы всегда можете написать мне в whatsapp.

