Движение точки в сопротивляющейся среде
При изучении движения материальной точки обычно подразумевают под такой точкой центр масс твердого тела. При движении твердого тела вблизи поверхности Земли, на его движение оказывает существенное влияние сопротивление воздуха.
При движении небольших объектов с малыми скоростями основная часть сопротивления обусловливается трением тел о воздух, и сопротивление воздуха можно считать пропорциональным первой степени скорости. В тех же случаях, когда тела имеют более внушительные размеры, сопротивление обусловливается инерцией среды, в которой движется точка или тело. Можно считать, что в этом случае сопротивление воздуха пропорционально квадрату скорости. При скоростях, близких к скорости звука, перестает быть достоверным и квадратичный закон сопротивления. В этом случае сопротивление воздуха определяется или по закону Сиаччи (1839—1907), что делается обычно в артиллерийских расчетах, или по какому-либо другому закону, устанавливаемому экспериментально.
Закон Сиаччи в общем случае можно представить в виде
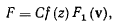
где 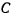 — коэффициент, зависящий от формы тела;
— коэффициент, зависящий от формы тела; 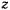 — высота тела над уровнем моря,
— высота тела над уровнем моря, 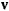 — скорость.
— скорость.
Рассмотрим сначала такое движение, при котором силу сопротивления воздуха можно принять пропорциональной первой степени скорости точки. Выберем оси координат так, чтобы ось 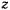 была направлена вертикально вверх, а ось
была направлена вертикально вверх, а ось 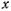 — по горизонтали так, чтобы начальная скорость лежала в плоскости
— по горизонтали так, чтобы начальная скорость лежала в плоскости 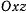 . Тогда уравнения движения запишутся в виде
. Тогда уравнения движения запишутся в виде
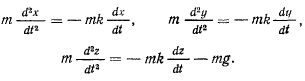
Все три уравнения движения можно проинтегрировать независимо одно от другого. В результате интегрирования получим
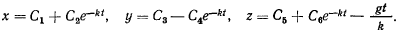
Постоянные
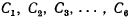
определяются из начальных условий при
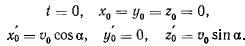
Значения постоянных С, находим, решая следующую систему уравнений:
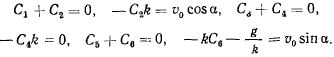
Решение, соответствующее этим начальным данным, приобретает вид
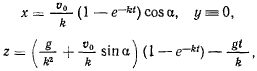
откуда следует, что точка будет двигаться в плоскости 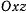 . Исключив отсюда время, получим уравнение траектории.
. Исключив отсюда время, получим уравнение траектории.
В баллистике большое значение имеет задача о движении материальной точки при квадратичном законе сопротивления. В этом случае, выбирая оси координат как и в предыдущей задаче, уравнения движения запишем в виде
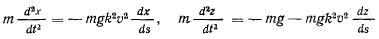
(движение происходит в плоскости 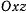 ). Преобразуем первое уравнение системы к виду
). Преобразуем первое уравнение системы к виду
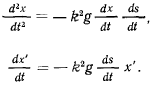
Разделяя в этом уравнении переменные
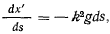
после интегрирования получим
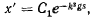
где 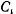 определяется из начальных условий
определяется из начальных условий
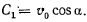
Обозначая через 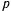 тангенс угла наклона касательной к оси
тангенс угла наклона касательной к оси 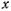
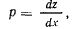
будем иметь
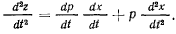
Тогда уравнение движения запишется в виде
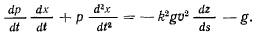
Подставив сюда 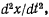 получим
получим
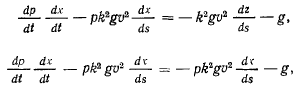
что после упрощения дает
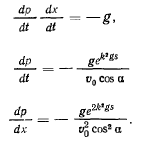
Заменяя
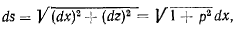
получим
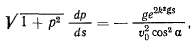
т. е. приходим к уравнению с разделенными переменными. Введем обозначение
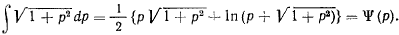
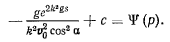
Тогда интеграл уравнения можно будет представить в виде
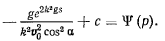
В начальный момент
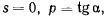
откуда
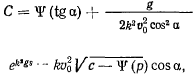
после чего уже можно определить 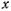 и
и 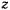 . В самом деле,
. В самом деле,
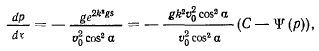
откуда
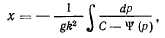
далее
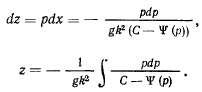
Для вычисления двух последних интегралов существуют специальные таблицы.
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Движение тяжелой материальной точки в пустоте |
| Движение материальной точки под действием центральных сил |
| Движение несвободной материальной точки |
| Относительное движение материальной точки |

