Оглавление:







Движение точки по неподвижной или движущейся поверхности. Общие положения
- Уравнение движения. Учитывая поверхность S, которая может изменять как положение, так и форму f x, y, 2, f = 0 1. Равенство этой поверхности в декартовых координатах. Координаты x, y, Z находятся под действием заданной силы, где имеется проекция X, Y, Z на результирующую F, где точка M масса x, y, Z, скользящая без трения по этой поверхности. Движение точки.
Со стороны поверхности обычная реакция N действует на точку, проекция которой будет представлять собой величину формы: Северный Эту точку можно считать свободной под действием сил F и N. уравнение движения выглядит так: Эти уравнения, наряду с уравнением 1 поверхности, образуют систему из 4 уравнений, которые определяют x, y. функция t z и Чтобы найти уравнение, определяющее x, y, z в функции, необходимо исключить X из уравнения 2, которое будет представлять собой 2 уравнения. После того, как движение найдено, значение X, а следовательно, и величина реакции, могут быть найдены из любого уравнения 2 системы или комбинации этих уравнений. уравнение Лагранжа.
Рассмотрим точку М, притягиваемую неподвижным центром О по закону обратной пропорциональности квадрату расстояния. Людмила Фирмаль
Метод Лагранжа, описанный в дальнейшем, аналогичен методу, используемому для исследования движения точек вдоль кривой раздел 259. всегда можно представить координаты точки На поверхности S, в частности точки M, как функцию от 2 параметров. х = .4и ЧР о. г = В В2.т, з = з гв Т гв. 3 эти формулы получаются снова, если q2 также исключается. Уравнение поверхности 1.Они явно включают время t, которое входит в уравнение 1.в некоторых случаях, когда поверхность S не работает, уравнение 1 не включает время, а уравнения для x 3, y и z также явно не включают время. Чтобы знать движение, достаточно знать, как параметр Q2, определяющий положение движущейся точки, выражается в терминах t.
Чтобы найти qx и q2, нужно выражение 2.Это может быть сконфигурировано следующим образом: уравнение умножения 2, соответственно, DX do dz на Т—.Если вы добавите их, они будут выглядеть так: йй, йй, йй. 4 Куда В этом уравнении коэффициенты исчезают из за соотношения о ДХ ДФ ду ДФ ДХ ДЗ dqx делать dqi ДЗ dqx Это означает, что если Нормаль поверхности нормальна, сохраняя q2 и константу, и изменяя параметр qx только, если эта кривая находится на поверхности S, то она соответствует кривой, описанной точкой 3.Аналогично уравнению движения 2 dx dy dz в дополнение к J получаем уравнение 4 Куда Выражения 4 и 4 определяют qx и q2 функции I. Они могут быть записаны в гораздо более простой форме.
Представляют собой производные qx и q2 для t и x. Y, Z проекция dx dy dz di dt dt точки. Формула 4, очевидно Но. через ц Исходя из равенства 3, x напрямую зависит от t, а q2 является функцией. И так оно и есть. дх я ДХ Просто так. То же. дуплексный Т зависит от прямого 6 через ц И q2 соответственно икс., Dqidt л Вес йй 1 dqidqi ч 9 В уравнении 6 мы видим x как функцию переменных Q2, q , q2, т. затем находим его ДХ ДХ ДХ d2x ,. ЦТ., Д х dq dq dqi d4l dq, d91 dt Т. е.
Аналогичный расчет дает следующие результаты: Делать у у д у dqx d h dqv di dq dz ДЗ ДЗ ДЗ я dq x 0 l dt dqj9 Смещение величины уравнения движения 5 ДХ делать дз д ДХ г У Д ДЗ Когда эти значения найдены, мы получаем уравнение Или L dq t d9l Куда ты положил 1 7 Аналогично, если преобразовать уравнение 4 Уравнения 7 и 7 являются уравнениями движения Лагранжа. Получить them. It достаточно вычислить величину T, которая равна кинетической энергии точки. Для этой величины необходимо заменить x , y , zr на 6, чтобы представить T в терминах qv q2, q e q2 и t1.Затем можно настроить формулы 7 и 7. В этих уравнениях правые части Q и Q2 вычисляются выше.
Они также могут быть определены следующим образом: пусть точка возможного смещения вдоль поверхности S, то есть пусть t постоянна и пусть смещение оказывается равным величине qx и q2, с приращением Zqx и q2.Проекция этого возможного движения на координатные оси является DX 5 л ды, ды ДЗ. ДЗ 4 Итак, принимая приведенные выше значения и Q2, получаем следующее уравнение для возможной силы F: Xbx по Дж г Страна З 62 = БС + К2 lq2. Поэтому для нахождения величин и Q2 достаточно определить коэффициенты в oqx и oq2 относительно возможной работы силы F для любого перемещения, происходящего на поверхности 5 в положении, занимаемом поверхностью в момент времени t.
- В частности, чтобы получить Qp, вам нужно уведомить точку возможного displacement. Получается, что если вы держите Q2 и T постоянными, и только qx изменяется на величину его колебаний, то возможная работа соответствующей силы F будет Q qx. Аналогично, чтобы получить Q2, qx и t2 должны принять постоянное возможное смещение, а работа силы F равна Q2c q2. Если функция силы U x, y, z присутствует, или если выполняется более общее условие, X, Y, Z является частной производной функции U x, yt, z, t t, которая включает время, и фактически U x, y, z, T является частной производной функции U x, y, Z, T , потому что она зависит от x, y, ду di dh .d Ts dy idU ДЗ в DX, в ды.
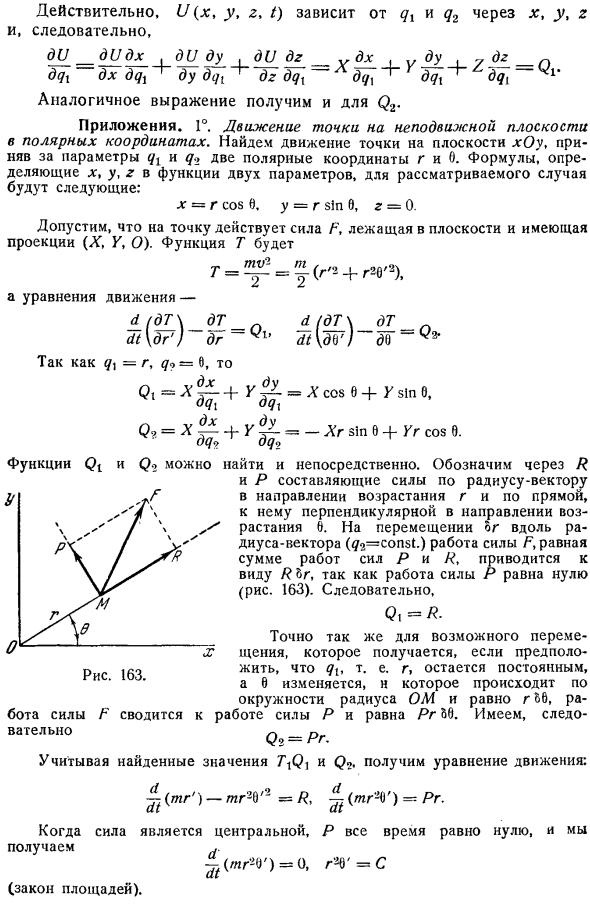
Мы получаем аналогичное выражение для Q2. Приложения D. движение точки на неподвижной плоскости в полярных координатах. Найдем движение точек на плоскости xOy с 2 полярными координатами r и 0 в качестве параметров QX и q2.Выражение, которое определяет x, y и r в функции 2 параметров, выглядит так для рассматриваемого случая: х = cos0 р г = р грехе 0,р 0 Предположим, что сила F, находящаяся в плоскости и имеющая выступы X, Y, О, действует как точка. Функция T является Р = := .x2 bg20, 2х d t Д7 вопрос Уравнение движения d t модель QX = р, м = 0. Q, Y x cos0+ Y sin 0 д 7и dqt Q,= X + Y sinsin 0 + yr cosв.
В этом случае говорят, что для проекции движения на плоскость ху справедлива теорема площадей. Людмила Фирмаль
Особенности Qi и Q можно найти непосредственно. R и P обозначают компонент силы вдоль радиус вектора в направлении увеличения r, а компонент силы по прямой, перпендикулярной направлению увеличения 0.При движении или усилии вдоль радиус вектора 2 = const. Работа силы F равна сумме сил P, а работа силы P равна нулю, поэтому R сводится к виду R br рис.163. так… Кварта.
Аналогично для возможных перемещений, то есть если r остается постоянным, происходит вдоль окружности радиуса OM и предполагается изменение 6, которое равно r 6 Сводится к работе силы Р и равна пр РБ. Есть следы К2 = пр. Найдено значение TXQX j mr mr2V2 = Когда сила приходит в центр.. Wf2U = О Заставили ботов в Рассматриваемый И Q2.Получаем уравнение движения: = Pr. P всегда равно нулю ГСВ = с Закон квадратов. O угол y или 2.Найти движение без трения тяжелой точки на плоскости, которая равномерно вращается вокруг горизонтальной оси, расположенной в этой плоскости. Он отсчитывает время с момента, когда плоскость вращения совпадает с плоскостью xOy. Предположим, что это горизонтально.
Возьмите ось вращения в качестве оси X.0 = at, где el угловая скорость шестерни. Уравнение скорости вращения, ROx грех З что при = 0. Вычислите уравнение движения, применив общую формулу 262. Т Ф mdfi = хз, н 0 Запретные зоны т ДТ C0S 164, заместитель Кроме того, обычная реакция Значение равно k. To зафиксируйте положение точки M на движущейся плоскости, используя координаты x и r осей Ox, или, где x параметр qlt, а r параметр Q2. Х = х, т р сов в, 2 = Р грех по. И функция t Мы получаем r = i. m x 2 + r 2 + V. Электрический ток И так оно и есть. сила, что mg имеет степенную функцию O = mg g = mgr sin at. д р ДХ mxdx Или dT Д7 = г н д р ДХ ду д р. Да. мг греха со.
Уравнение движения выглядит так: первое из этих уравнений показывает, что проекция Q точки M на ось x движется равномерно. 2 е уравнение является линейным с постоянным коэффициентом, интегрируется и имеет общий Интеграл g = Aeat 4 Be nt h a Sin at. 2 о Чтобы найти уравнение проекции траектории на плоскость YZ, достаточно заменить угол 0.In эти отношения Р = ае + быть Джей Сино. Особенно интересно, когда начальные условия A и B равны нулю. Поэтому достаточно, чтобы точки были отлиты от оси вращения так, чтобы проекция на прямую R имела начальную скорость, равную 2.Тогда уравнение проекции траектории на плоскость yz выглядит следующим образом: р = с, ч0.
Это касательная окружности в точке O на оси OY. Орбита будет вращаться по спирали. Возьмите 1 из уравнения движения снова, чтобы вычислить нормальную реакцию. Рутений. м = к sinw. Если вы замените это значение на r cos a Поэтому вспомним уравнение, определяющее r РГ = 02Г Синко Мы получаем Х = мг в COS о 2 Жо. замените r на его значение эта формула определяет нормальную реакцию функции T.
Смотрите также:
Решение задач по теоретической механике

