Движение точки на плоскости. Система дифференциальных уравнений

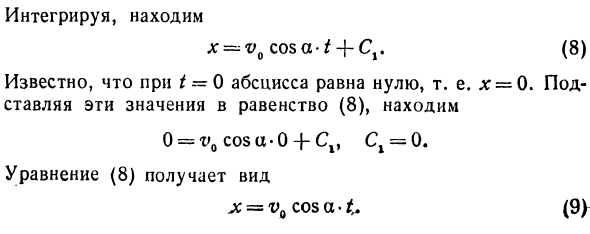
Движение точки на плоскости. Система дифференциальных уравнений

• Движение точки на плоскости. Система дифференциальных уравнений Заставьте точку P массы m двигаться на плоскости под действием силы F, которая изменяется как по величине, так и по направлению. Чтобы исследовать это движение, точка P проецируется на оси координат и учитывается движение этих проекций вдоль оси. Таким образом, задача перемещения точки на плоскости учитывает два движения вдоль координатной оси.

Далее проекция силы F на ось Ox (обозначается X) X-F cos a А проекция силы F на ось Oy (обозначается Y) равна K = / 7sin a. Проекции скорости v на оси Ox и Oy обозначены через vx и v ‘соответственно, а проекция точки P на оси Ox и Oy — Px и Ru. Есть Px (x, 0) и Py (0, y). Согласно §4, вы можете написать: DX_ DY _ dt ~~ di UU dvx _ d * x ~ DT ~ dtil dvy_d * y ~ dt « df * ‘ DVX V tj = x> dt д * х m- = X = F cosa, м = к = ^ грех а. АТ2 Поэтому движение точки на плоскости определяется двумя дифференциальными уравнениями (4J и (4t)).

Угол, образованный силой F, представлен положительным направлением оси Ox и a (этот угол является переменной величиной). Людмила Фирмаль

Может быть удобнее использовать уравнения (3J и (32)). Уравнения (4,) и (42) называются дифференциальной системой точечного движения на плоскости. Пример 1. Если вы знаете, что объект брошен с начальной скоростью v0 под углом a относительно горизонта от начала координат, рассмотрите движение материальной точки P под действием силы тяжести F в пространстве без воздуха. Выберите оси координат так, чтобы ось быков была горизонтальной (Рисунок 111). / // 7 Тысина L / 1 Lee U Ох и 0 cosx p * JP Рисунок 111

Во время движения в точке P. действует только сила тяжести F, равная мг. Где m — масса точки, а g — ускорение силы тяжести. Гравитация направлена ​​в отрицательном направлении оси Oy. Другие силы не действуют на очки. Проекция силы F на ось Ox равна нулю, а на ось Oy равна (-mg). Следовательно, уравнения в этом случае (4J и (42) записываются в виде: д * х л д2й Это система двух квадратичных дифференциальных уравнений.

• Однако удобнее использовать уравнения (3) и (3r), то есть систему дифференциальных уравнений первого порядка. Система для рассматриваемой проблемы: dvv v * Т? -Mg. (5) Уравнение (из 5J: ^ = 0; это означает, что vx всегда содержит постоянное значение. Кроме того, так как первый момент = cos a, всегда Hoi; x = ~; поэтому перепишите уравнение (6) в следующую форму: ~ = Z> 0cosa или dx ^ v ^ zosadt. (7) vx = v0 cos a. (6) х — дт Я дт

Интегрировать и найти x = ^ v0 cos a -Z + Cj. (8) Известно, что абсцисса равна нулю, т.е. х = 0. Подстановка этих значений в уравнение (8) дает 0 = i> 0cosu-0 + CV Cx = 0. Уравнение (8) принимает следующий вид: ^ = x ^ 0cosa- ^ (9) (10) Поскольку t = 0 и vy = v0 sin a, из (10) v0 sin a = -g-0 + C2, Cr = g; 0 sin a.

Из уравнения (5t): или dvy = -gdt. Интегрируй и получай v, = -gi + Ct. Людмила Фирмаль

Уравнение (10) принимает следующий вид: vy = — gt + vQ sina или 57 = — + sin a- интеграция, наконец, последнее уравнение, J = — ^ + *. Сина. <+ Ct. (А) Поскольку ордината также равна нулю при / = 0, замена значений (11) / = 0 и ^ = 0 приводит к Ct = 0. После этого уравнение (11) уже принимает окончательный вид. у = — ^ + в0ситиат. (12)Уравнения (9) и (12) определяют движение точки, наклоненной к горизонту под действием силы тяжести. Эти уравнения являются гл. 111.

Смотрите также:

Предмет высшая математика

Дифференциальные уравнения первого порядка	Определители (основные понятия)
Некоторые дифференциальные уравнения, встречающиеся в механике	Свойства определителей