Оглавление:




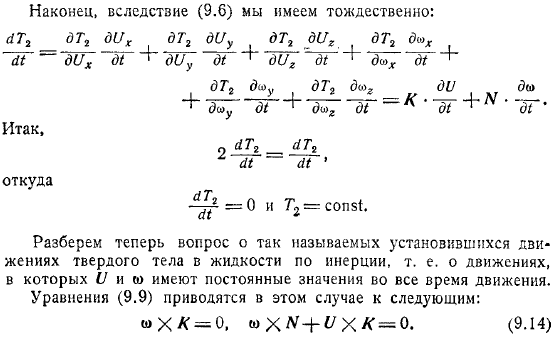

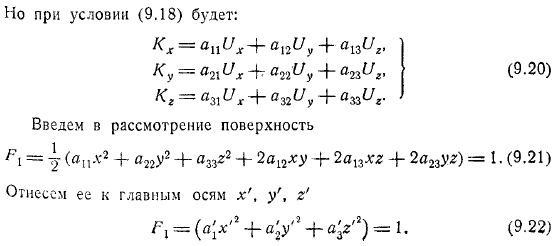


Движение тела по инерции
Вернемся к общему случаю, когда жизненная сила жидкости определяется по формуле. Если на тело не действует внешняя сила, то возникает вопрос о движении твердого тела в жидкости за счет инерции. Для простоты ориентируем ось гидромеханики координат вдоль главной оси инерции этого объекта, принимая центр инерции твердого тела за начальную точку движущейся системы координат.
Тогда для твердой жизненной силы получим следующую формулу. Где находится масса тела? Главный центральный момент инерции. Основной вектор примера импульса твердого тела и основной момент импульса для выбранной начальной точки определяются по формуле.
- Вводит обозначение для жизненной силы полной системы, состоящей из твердого и жидкого вещества. Понятно, что коэффициенты только в том виде заменяются другими.
- Кроме того, мы называем его вектором. Сила удара, и вектор импульсивная пара.
В результате получаем следующую формулу. Уравнения движения теперь описываются в простой форме. Людмила Фирмаль
Если нет внешней силы, то это выглядит так. В движущихся осях, повторите предыдущий аргумент, чтобы получить следующее уравнение. Легко показать интеграла этой системы.
Если умножить первое уравнение на скаляр, то получим. Отсюда этот интеграл наглядно показывает инвариантность величины ударной силы. Это следует непосредственно из первого уравнения. Это означает, что вектор имеет постоянное значение и постоянное направление в постоянной системе координат.
- Аналогично, умножьте первое уравнение системы на скаляр и умножьте последнее уравнение на оба полученных уравнения.
- Этот интеграл представляет собой инвариантность проекции импульса ударной пары относительно направления силы удара. Наконец, явный интеграл системы.
На самом деле, если мы умножим первое уравнение системы на скаляр, а затем умножим на скаляр, и оба полученных уравнения. С другой стороны, то есть квадратичная форма по теореме Эйлера для функции того же порядка от. Если мы используем это равенство для дифференцирования, то получим.
Наконец, в результате, имеют одинаковую идентичность. Людмила Фирмаль
Теперь рассмотрим вопрос о проблеме так называемого стационарного движения твердого тела в жидкости по инерции, то есть движения, имеющего постоянную величину на всем протяжении. В этом случае типы волн уравнение сводится к.
Но из этих соображений только являются. Факт, первое уравнение эквивалентно. Показано, что мгновенная ось вращения направлена вдоль силы удара. Из последнего уравнения вы можете видеть. А потом это продолжается. Дано и получено линейных однородных уравнений.
Как насчет линейной функции с постоянными коэффициентами? Для того чтобы предыдущая система имела решение, ее определитель должен быть равен нулю. Этот определитель является многочленом порядка. Установить произвольно, чтобы определить величину из эквивалента от нуля данного определителя и найти все величин из системы до определенного коэффициента.
В частности, рассмотрим следующие случаи. Он имеет дело с поступательным движением. В этом случае система сводится к простому виду, но условия таковы. На главной оси. В этой системе осей выражение принимает следующий вид. Уравнение выглядит так.
В общем случае, когда все отличается друг от друга, возможны следующие значения. Это соответствует поступательным движениям в направлении главной оси поверхности. Таким образом, в общем случае в случае твердых тел существует только взаимно перпендикулярных направления, в которых может быть выполнено поступательное инерционное движение.

