Оглавление:






Движение по инерции твердого тела, имеющего неподвижную точку
- Твердое тело, вращающееся вокруг неподвижной точки, имеет 3 степени свободы. Его местоположение можно определить по 3 углам Эйлера. Основной момент импульса твердого тела относительно координатных осей задается следующей формулой, так как начальная точка находится в неподвижной точке Лы ыыы-лы, — ЛР — о, —1y1 АР осевой и центробежный моменты инерции твердых тел изменяются при фиксированных осях x, y и z. Если оси x, y и z строго связаны с движущимися твердыми телами, то их ось и центробежные моменты инерции постоянны. Если ось x, y, z является главной осью инерции твердого тела в неподвижной точке, т. е.
Если xy 0, то выражение принимает вид ЛК х0 х, и ly ой, Лк 1 р Где ix, ly-главный момент инерции твердого тела относительно неподвижной точки. Форма жесткого динамического уравнения Эйлера, вращающегося вокруг неподвижной точки проекции на оси x, y и z, связанной с движущимся твердым телом, выглядит следующим образом 0yl — 0ilj. Икс 2. Терабайт. L. 4.
Направим ось х вдоль пружины по вертикали вниз, взяв начало отсчета в положении статического равновесия груза. Людмила Фирмаль
Главный момент внешней силы на оси Координаты i от x, og-проекция угловой скорости твердого тела на координатные оси. Если ось x, y, z, связанная с твердым телом, является главной осью инерции в неподвижной точке, то динамическое уравнение Эйлера описывается как Л- у ф г А 4-4 о 0ж. 4 −4 0×0 В4. Добавьте к этим 3 дифференциальным уравнениям уравнения движения Эйлера, которые представляют зависимости между соответствующими осями, углами Эйлера и проекциями угловой скорости их производных по времени. Sin 9 sin 6 при cos, б у sin при cos 0-6 sin, Е З я cos6 ИЖ Получилась система из 6 обыкновенных дифференциальных уравнений движения.
Интегрируйте эту систему уравнений если существуют начальные условия движения, чтобы определить уравнение вращения твердого тела вокруг a y, a r и неподвижной точки. A 0, a e 3 0- Решение обратной задачи динамики твердого тела, вращающегося вокруг неподвижной точки, сопряжено с большими трудностями и может быть сведено ортогонально только в исключительных случаях. Форма обобщенного динамического уравнения Эйлера для движущейся оси, не связанной с твердым телом дю — Р 0lnlj-cngd смотрите игру otj длн — Унция Н. Е.
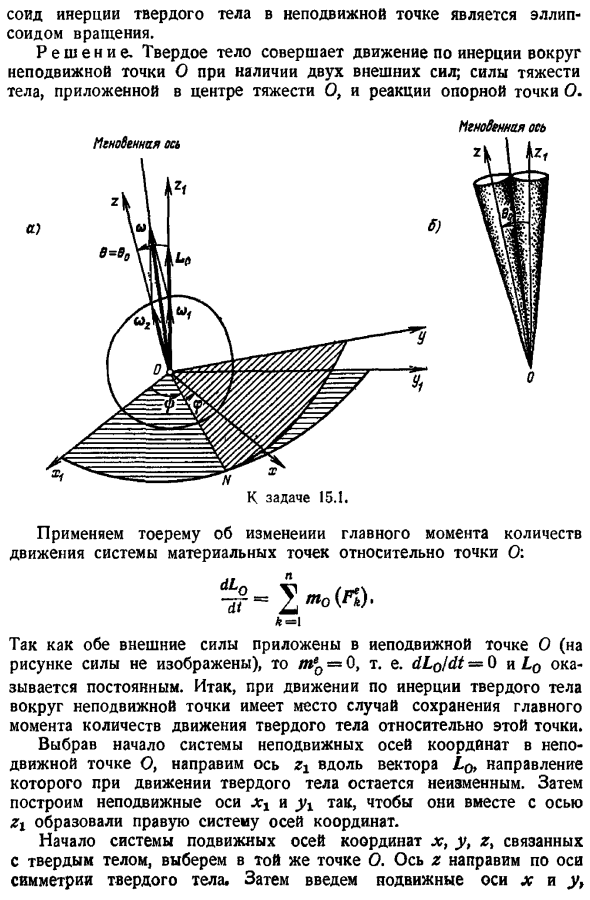
Главный момент внешней силы относительно оси движения, m, он не связан с твердым телом, Ц, Ц, а Ц — главный момент импульса твердого тела относительно оси и 1 q, 01n, w1e-проекция скорости трехстороннего вращения движущейся оси. Задача 15. 1. Исследуйте инерцию твердого тела, в котором центр тяжести выровнен по неподвижной точке. Эрин. Инерционная жидкость твердого тела в неподвижной точке представляет собой сфероид. Решение. Твердое тело движется по инерции вокруг неподвижной точки o, при наличии 2 внешних сил. Сила тяжести объекта, приложенная к центру тяжести o, и реакция опорной точки o Мгновенная ось К заданию 15. 1.
Применим фиксированную точку к изменению основного момента импульса материальной точечной системы относительно точки О. Поскольку обе внешние силы приложены к неподвижной точке О сила не показана на рисунке, мы можем видеть, что тоо 0, то есть dloldt 0, а lo является постоянной величиной. Поэтому при движении по инерции твердого тела вокруг неподвижной точки основной момент движения твердого тела относительно этой точки может сохраняться. После выбора начала координат системы неподвижных осей координат в неподвижной точке О, укажите ось zj вдоль вектора lo, где ориентация не изменяется во время движения твердого тела.
- Затем постройте фиксированные оси xt и yt так, чтобы они образовывали правильную систему осей вместе с осью zi. Начало координат координат x, y и z, связанных с твердым телом, выбирается в той же точке o. Укажите ось z вдоль оси симметрии твердого тела. Затем введите подвижные оси x и y. Это главная ось инерции в точке О см. Рисунок а. Поскольку эллипсоид инерции является сфероидом, , ,. Запишите динамические и кинематические уравнения Эйлера для 1 — 1y и т х tag 0 m o-ty lx x.
Кинетическая энергия твердого тела вращающегося вокруг неподвижной точки Р г, о, О1 Первый Интеграл 7 подразумевает постоянство кинетической энергии твердого тела этот результат равен нулю, поскольку является суммой работы внешних сил, которую легко получить с помощью теоремы об изменении кинетической энергии материальной точечной системы, так как внешние силы приложены к твердому телу в неподвижной точке. Чтобы определить другой первый Интеграл, умножьте уравнение 1 на о, уравнение 2 — на уОу, уравнение 3 —. После добавления его, вы получаете 1 b 0, pyoufu 4 0 0 0 Иначе говоря x 1 zx 0 Отсюда 8 cs-константа.
Итак, при последовательном соедине-пии пружин податливость эквивалентной пружины равна сумме податливостей данных пружин. Людмила Фирмаль
Нетрудно заметить, что первый Интеграл, записанный в Формуле 8, показывает инвариантность модуля модуля главного момента в сумме. 9 Движение твердого тела относительно неподвижной точки o. in фактически, оси x, y и z являются главной осью инерции твердого тела в точке o, поэтому по-fywj -, Б, , поэтому 7d0 Х Л Х ЛГ ЖЖ Л С. Для упрощения интегрирования системы дифференциальных уравнений 3 — 6 проекция основных моментов импульса твердого тела, учитывающая положение вектора lq, записывает lx, ly, lt на подвижные оси x, y и z, связанные с твердым телом на оси zi см. Рисунок а. После проектирования оси lo и qxyz Л 1-о СЛН 8 грех п т0 грех 8 с cos Р, ЛР З. О. Кос 8.
Используя выражение 9, перепишите выражение 10 в следующий вид lo sin 6 sin p, 11 ycuj, lo sin 8 cosф, 12 Ху ло, потому что 8. 13 Из дифференциального уравнения 3 видно, что w является постоянной величиной. Если в первый момент вы переместите a x, то w a1. Они Из Формулы 13 И Где lo v z-1 1j lj y y 1. Jwj. R-константа. Поэтому lt4 t, lo также являются константами, и предварительно записанный угол в движении твердого тела не изменяется. 0 6 15 Это следует 16 17 18 6 0.
Теперь уравнение 4 — 6 можно записать короче Вт, фsin 80 sinф, а у фsinв0cosф, фcosв, ф. Подставляя значение хивв в формуле 16 в формулу 11, а значение a y в Формуле 17 в формулу 12, получаем результат. Его sin 60 56 0, а угол может принимать разные значения. Примечание Ло 7×7-О и 7j я- o 1, 19 То есть, прецессия осуществляется с постоянной угловой скоростью Если мы интегрируем формулу 19, то получим 014 если 4 0, то 0. 20 Подставляя величину coj в уравнение 18 вместо ш, — oicosso.
Так что f-это константа. После введения обозначения О -Е 1, потому что н0 з Ф ОЛ, 21 То есть постоянная угловая скорость 0С. Интегрируем формулу 21 и запишем ее для 4 0, p 0. 14 h 0 Так, при инерционном движении симметричного твердого тела, где центр тяжести совпадает с неподвижной точкой, происходит упражнение, называемое обычным precession. It определяется уравнением 6 b0, 14 0, 4 0. Ось r симметрии твердого тела представляет собой конус, угол вершины o которого равен 26о, а угловая скорость op. It имеет угловую скорость s2. Вектор мгновенной угловой скорости o см. Рисунок a, который представлен диагональю параллелограмма, состоящего из векторов o i и w, расположен на мгновенной оси.
При движении твердого тела параллелограмм угловой скорости остается постоянным числом и вращается вокруг оси zt с постоянной угловой скоростью. Velocity. In другими словами, ось симметрии твердого тела, z, представляет собой конус, центрированный на оси zt. Неподвижный осевой выступ представляет собой конус, описываемый мгновенной осью вокруг оси zt см. Рисунок b. Подвижный вал представляет собой конус, который описывается мгновенной осью вокруг оси z.
Смотрите также:
Предмет теоретическая механика

