Оглавление:



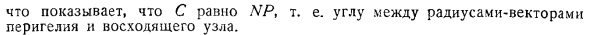

Движение планеты в сферических координатах по Якоби
- Возьмем плоскость X Y эклиптики, прямую линию, соединяющую солнце с весенним равноденствием оси x, и определим положение планеты по ее сферическим координатам r, cp, cp. Где Phi долгота планеты, cp Его широта рис. 177а. Подобно астрономии, ось ориентирована. Переменные r, p и cp играют роль параметра QB q q. Для функции силы существует 7= , и масса планеты считается единой.
Из сферического уравнения координат ds2, непосредственно Следующий Заменять С08ср Значение р, г, ср т найти здесь n = t и тогда— 1пр1 ПЛ 1 G2 G2 COS2 sr Я Г Таким образом, PDE W выглядит следующим образом: 1, 1 dW 2, 1 и 2 л д р Дж Р Р2 ды + cos2 Р2 ть й р + 1 В этой конкретной форме уравнения 1 можно найти полный Интеграл в виде: У7 = 4.4 Т Где R, Phi и W переменные r, функция ЦФ. Для того чтобы U7 удовлетворяло уравнению 1, необходимо: 1. G2 COUS2 вода После разделения терминов в r это выражение можно записать в виде: г Левая сторона зависит только от cf и f, а правая только от G.
Найдем, при помощи какой кривой С нужно соединить эти две точки для того, чтобы тяжелая материальная точка, пущенная из точки А без начальной скорости, скользя по этой кривой, достигла точки В за наиболее короткий промежуток времени. Людмила Фирмаль
Таким образом, в уравнении 1 переменные r, y и PHI независимы, поэтому это уравнение возможно только в том случае, если каждая часть равна одному и тому же постоянному значению O2 индивидуально. Поэтому мы имеем 2 =2Л+. А = 2Н + д р И затем ф 2 L J1Г 2 4кв. COS2 вода Или Y 2 = G2 f 2 COS2 Повторяя те же рассуждения выше, мы видим, что обе стороны последнего уравнения должны быть равны 1 константе 2 отдельно. Результат Т = л, т = ф Таким образом, полный Интеграл уравнения 1 равен, а конечное уравнение движения имеет вид: ДЛТ ДГ, ДГ 4. dG C DL Z b Иначе говоря в г первые 2 уравнения, которые не содержат t, определяют trajectory.
- To дополните решение, укажите значение констант, содержащихся в этих выражениях. Мы знаем, что орбиты планет эллиптические. Максимальные и минимальные радиус векторы, соответствующие афелию и перигелию, равны a 1 f g и a 1 e .С другой стороны, формула III имеет вид Таким образом, корни Радикальной формулы должны соответствовать максимальному и минимальному значениям радиуса vector. So, эти маршруты равны q 1 и q 1 e , исходя из соотношения между маршрутом и коэффициентом А = Г2 = ва е = ИИП, г = В З Я думаю, что это хорошо idea. To получим действительное значение из уравнения II , когда функция y задана, то неравенства достаточно.
Кроме того, для каждого значения y, удовлетворяющего этому условию, соответствующее значение 7, определенное из уравнения I , должно быть вещественным числом, поскольку траектория является реальным эллипсом. Таким образом, u имеет верхнюю границу arccos, и этот предел может быть достигнут. Но очевидно, что максимальное значение угла 9 это угол I между плоскостью орбиты и плоскостью эклиптики =со з, = со. Далее необходимо установить нижний предел интеграла. Используйте r = l 1 e для перигелия и y = 0 для узла N. тогда уравнение III указывает время, необходимое для 0, чтобы пройти перигелий, и уравнение II. ф0 это долгота узла.
Мы видели, что таутохронная кривая определяется с точностью до постоянных, когда требуют, чтобы таутохронизм имел место отдельно для двух различных законов сил при одной и той же точке таутохронизма для обоих законов. Людмила Фирмаль
Чтобы вычислить C, мы предполагаем, что планета является перигелием. Тогда выражение I будет выглядеть следующим образом: Пирог Дж Где Y широта перигелия. Учитывая связь между L = g cosZ, вы можете написать: Так и есть cos y z y j cos2 Z COS2 Или интеграция Смола 7 I =С, sinc.= грех з деше. грех я ТЛ Пусть N и P рис. 1776 точки пересечения сферы и восходящего узла и радиус вектора перигелия с радиусом 1, центрированным в точке O, и пусть PQ =перигелий latitude. In треугольник NPQ грех = грех НП Синс.
Смотрите также:
Решение задач по теоретической механике

