Оглавление:
Движение материальной точки под действием центральных сил
Основные положения
Рассмотрим движение материальной точки, находящейся под действием силы, линия действия которой все время проходит через неподвижную точку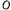 
, принимаемую за начало координат. Такая сила, называемая центральной, может либо притягивать материальную точку к неподвижному центру 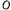, либо отталкивать ее от этого центра.
Отталкивающую силу условимся считать положительной, а притягивающую— отрицательной. Выше было установлено, что точка, движущаяся под действием центральных сил, описывает плоскую траекторию. Поэтому всегда можно систему неподвижных осей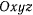 
выбрать так, чтобы плоскость движения точки совпадала с плоскостью 
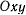. В дальнейших рассуждениях координаты движущейся материальной точки будем обозначать через 
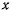и 
.
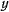Так как для центральной силы момент относительно центра силы всегда равен нулю, движение будет происходить по закону площадей и будет подчиниться закону площадей
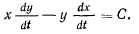
Здесь в левой части имеем момент вектора скорости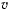 
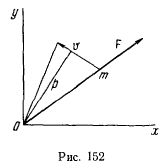
точки относительно начала координат, поэтому постоянная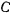 
по величине равна удвоенной площади треугольника (рис. 152), основанием которого служит вектор скорости точки, а вершина находится в центре сил. Другими словами
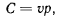
где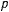 
— длина перпендикуляра, опущенного на линию действия вектора скорости точки.
Движение точки, вызываемое центральными силами, называют центральным движением. При изучении центральных движений бывает удобно ввести в рассмотрение полярные координаты точк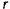и 
и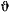 
при помощи формул преобразования
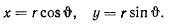
Тогда, полагая, что за время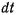 
полярный угол 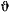изменится на величину 
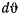, а полярный радиус 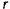— на величину 
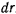, получим с точностью до бесконечно малых величин высшего порядка приращение заметаемой полярным радиусом площади за время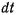
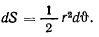
Удвоенная секторная скорость будет равна
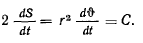
Кроме теоремы об изменении момента количества движения для исследования движения можно применить теорему живых сил, которая в данном случае запишется в виде
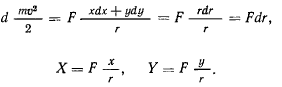
Если к тому же центральная сила зависит только от положения материальной точки и обладает силовой функцией, то существует интеграл живых сил
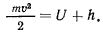
Таким образом, два первых интеграла — интеграл площадей и интеграл живых сил будут определять движение материальной точки, находящейся под действием центральной силы.
В задачах небесной механики применяется еще один векторный интеграл уравнений движения материальной точки, находящейся под действием центральных сил — интеграл Лапласа. Этот интеграл имеет место для центральной силы притяжения материальной точки к неподвижному центру, величина которой обратно пропорциональна квадрату расстояния материальной точки до притягивающего центра. Такую силу принято называть силой ньютонианского тяготения
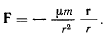
Здесь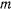 
— масса материальной точки; 
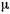— коэффициент пропорциональности. Уравнение движения материальной точки в векторном виде после сокращения на 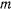можно записать так:
Если еще обозначить через с вектор момента количества движения материальной точки, разделенный на массу
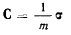
(вектор, перпендикулярный к плоскости движения материальной точки), то можно будет рассмотреть векторное произведение
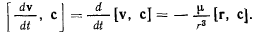
Но так как
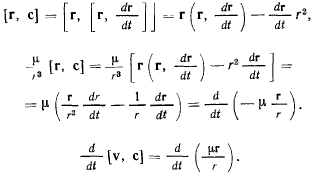
Отсюда следует еще один первый векторный интеграл уравнений движении материальной точки в случае центральных движений
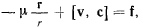
который называется вектором Лапласа. Можно показать, что интеграл площадей, интеграл живых сил и вектор Лапласа не являются независимыми величинами.
- Формулы Бине дают некоторые удобства при рассмотрении центральных движений. Для получения этих формул рассмотрим скорость движения материальной точки в полярных координатах
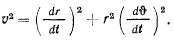
Определив 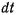из интеграла площадей
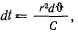
представим выражение для скорости в виде
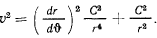
Если же сделать замену
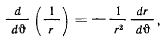
то выражение для скорости приобретет вид
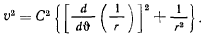
Полученная формула называется первой формулой Б пне для определения скорости материальной точки Формула позволяет определять скорость материальной точки, движущейся в центральном силовом поле, если известна траектория точки
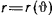
и ее секторная скорость.
Вернемся к теореме живых сил, которую запишем в виде
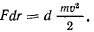
Разделив обе части этого равенства на 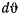и подставляя сюда выражение скорости, полученное из первой формулы Вине, найдем
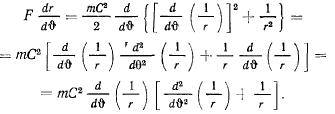
Подставляя в левую часть
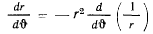
и сокращая на
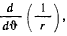
получим
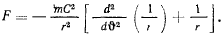
Эта формула носит название второй формулы Бине для определения центральной силы, действующей на материальную точку, если известны траектория точки и ее секторная скорость.
Формулы Бине позволяют разрешать и обратную задачу — нахождение тректорнн точки по заданной центральной силе, действующей на эту точку. В этом последнем случае задача сводится к интегрированию дифференциального уравнения второго порядка.
Пример:
Материальная точка массой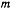 
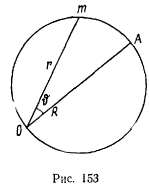
описывает окружность радиуса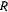 
. Какой должна быть центральная сила, если ее центр находится на окружности (рис. 153)?
Решение:
За полярную ось примем диаметр окружности, проходящий через центр силы. Тогда уравнение траектории запишется в виде
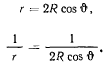
Вычислим производные от
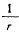
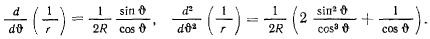
Подставляя эти значения в формулу Бине для силы, будем иметь
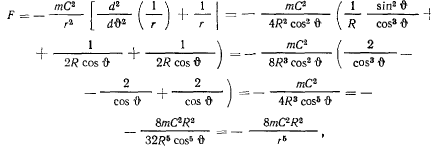
откуда видно, что на точку действует центральная сила притяжения, обратно пропорциональная пятой степени расстояния точки от притягивающего центра Величина силы зависит от закона движения точки по траектории. Если предположить, что » наиболее удаленной точке траектории скорость равна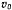 
, то постоянная площадей 
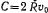и для силы получим значение
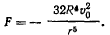
Пример:
Точка описывает эллипс
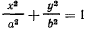
под действием силы притяжения к сто центру. Определить эту силу.
Решение:
Введем полярные координаты
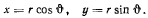
Тогда, заменив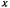 
и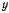 
в уравнении эллипса, получим
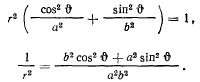
Вычислим производные от
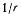
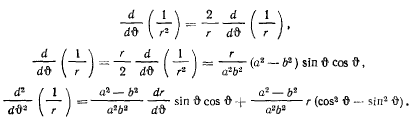
Подставляя эти значения в формулу Бине для силы, будем иметь
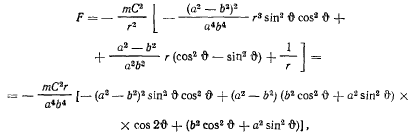
после приведения подобных членов
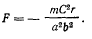
Сила будет полностью определена, если будет известен закон движения точки, для чего достаточно определить постоянную площадей.
- Задача о движении планет в течение многих лет является . одной из наиболее замечательных задач небесной механики, позволяющей определять положения небесных тел. С развитием исследований космоса эта задача получила новое значение в связи с тем, что свободные движения космических аппаратов совершаются по законам движения планет.
Законы движения планет были открыты выдающимся немецким астрономом Иоганном Кеплером (1571—1630), установившим эти законы на основании экспериментальных данных. Будучи изгнанным из Германии, Кеплер долго работал в Праге со знаменитым астрономом Тихо-Браге (1546—1601). Законы движения планет Кеплер установил, обрабатывая многочисленные наблюдения Тихо-Браге над планетой Марс.
Законы Кеплера
Все планеты и кометы движутся по коническим сечениям, в одном из фокусов которых находится Солнце.
- Площади, описываемые радиус-векторами планет относительно Солнца, пропорциональны временам движения планет.
- Для планет, движущихся по эллипсам, квадраты звездных времен обращения пропорциональны кубам больших полуосей, т. е.
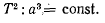
Законы Кеплера давали вполне ясную картину движения планет и показывали, что мир планет представляет собой стройную систему, управляемую единой силой, связанной с Солнцем. Но установить закон действия силы тяготения к Солнцу Кеплер не мог, так как еще не были известны основные законы механики. Впервые силу, действующую на планеты, определил Ньютон. Первые исследования Ныотона по этому вопросу относятся, по-видимому, к 1666 г., но окончательные результаты были опубликованы в 1687 г. в сочинении «Математические начала натуральной философии». Все свои рассуждения Ньютон проводил сложным геометрическим методом. При выводе закона тяготения будем пользоваться формулами Бине.
а) Вывод закона тяготения из законов Кеплера. Из второго и первого законов Кеплера следует, что сила, действующая на планеты, центральная, причем ее центром является Солнце. Из закона площадей
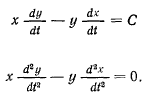
Определяя ускорения из уравнений движения
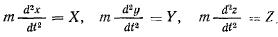
получим
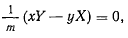
т. е. момент силы относительно начала координат равен нулю и, следовательно, эта сила центральная.
Первый закон Кеплера определяет орбиту и дает возможность определить силу при помощи формул Бине. В самом деле, записав полярное уравнение эллипса
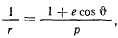
где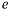 
— эксцентриситет эллипса
(
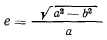
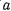и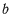 
— большая и малая полуоси эллипса), а 
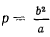— фокальный параметр, и подставляя это значение 
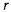во вторую формулу Бине, будем иметь
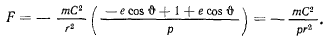
Таким образом, центральная сила, действующая на планету, — притягивающая и обратно пропорциональна квадрату расстояния планеты от Солнца. Величина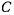 
удвоенной секторной скорости определяется из закона движения планеты.
Представим силу, действующую на планету, в виде
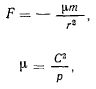
и покажем, что действующая сила прямо пропорциональна массам планет. Для этого предварительно необходимо показать, что величина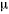 
одинакова для всех планет. Но величину 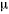можно представить в виде
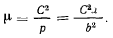
Принимая во внимание, что за период обращения радиус вектор планеты заметает всю площадь эллипса, получим
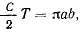
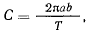
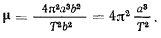
Отношение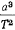 
по третьему закону Кеплера постоянно для всех планет, откуда следует и постоянство 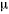для всех планет солнечной системы. Если же положить, что 
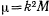где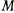 
— масса Солнца, то сила, действующая на планету, может быть представлена в виде
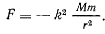
Величина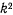 
также постоянна для всех планет солнечной системы. Она называется гравитационной постоянной, а сама величина 
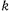называется постоянной Гаусса. В системе 
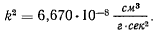
Полученный закон взаимного притяжения тела оказался справедливым не только для планет, но и вообще для всех тел природы.
б) Прямая задача Ньютона. Определение орбиты по заданной силе. После установления закона всемирного тяготения Ньютон обратился к следующей задаче:
Найти движение материальной тонки (планеты), притягиваемой неподвижным центром (Солнцем) с силой, обратно пропорциональной квадрату расстояния точки от притягивающего центра.
При решении этой задачи можно исходить непосредственно из законов движения материальной точки и искать решение последовательными интегрированиями. Удобнее исходить из первых интегралов уравнений движения. В рассматриваемом случае существует два первых интеграла уравнений движения: интеграл живых сил и интеграл площадей. Первый из них имеет вид
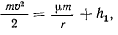
где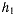 
— произвольная постоянная, определяемая из начальных условий. Разделив обе части равенства на 
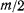, будем иметь
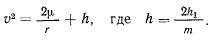
Определяя значение скорости с помощью первой формулы Бине, получим
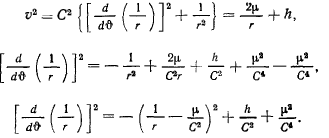
Это равенство получено из интеграла живых сил и выполняется во все время движения. Из него следует, что правая часть должна оставаться неотрицательной во все время движения, что возможно только тогда, когда
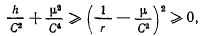
откуда следует, что
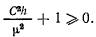
При помощи подстановки
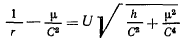
введем новую переменную величину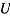 
и преобразуем дифференциальное уравнение траектории
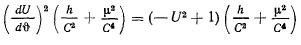
к виду
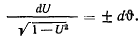
Интегрируя это уравнение, будем иметь
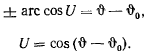
Возвращаясь к старым переменным, получим уравнение траектории в полярных координатах
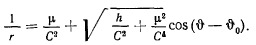
Сравнивая это уравнение с уравнением конического сечения
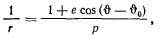
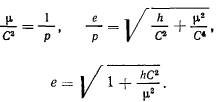
Последнее выражение для эксцентриситета позволяет определить вид конического сечения. Величина эксцентриситета, а следовательно, и вид траектории зависят от значения произвольной постоянной живых сил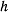 
. Из формулы для эксцентриситета видим, что
- при
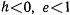— эллипс, - при
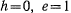— парабола, - при
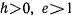— гипербола.
Постоянная живых сил
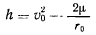
зависит от начального положения планеты и от величины начальной скорости. Очевидно, что эллиптические траектории имеют место лишь при ограниченной начальной скорости. Увеличивая скорость, будем получать параболические и гиперболические траектории.
Если постоянная живых сил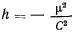 
, то для эксцентриситета получаем нулевое значение 
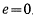. В этом случае траектория точки — окружность.
Пример:
Вычислить скорость точки, брошенной с поверхности Земли, необходимую для ее движения по круговой орбите вокруг Земли.
Решение:
Определим сначала величину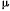 
для Земли. Вблизи поверхности Земли на точку действует сила
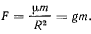
где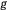 
— ускорение силы притяжения к центру Земли вблизи ее поверхности; 
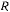— радиус Земли. Отсюда будем иметь
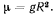
Величину начальной скорости точки определим из интеграла живых сил
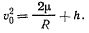
Подставляя сюда 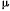, значение 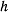для круговой орбиты и 
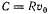, получим
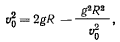
или
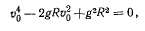
откуда
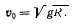
На поверхности Земли ускорение силы тяжести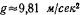 
, радиус Земли 
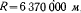, и тогда
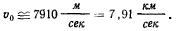
Скорость, с которой точка могла бы двигаться вблизи поверхности Земли по круговой орбите, называется круговой, или первой космической скоростью.
Второй космической скоростью, или парабол и-ческой скоростью, называют скорость, необходимую для того, чтобы тело преодолело земное тяготение и начало двигаться с поверхности Земли по параболической траектории.
Для определения второй космической скорости будем исходить из интеграла живых сил
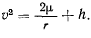
Для параболической траектории имеем 
и, следовательно, для определения начальной скорости на поверхности Земли будем иметь
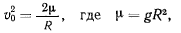
откуда
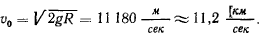
При скорости большей чем 11,2 км/сек точка будет двигаться по гиперболической траектории (рис. 154).
Здесь приведены расчеты в предположении, что на точку действует только сила притяжения со стороны Земли. На самом деле на точку действует сила притяжения со стороны Солнца, влияние которого вблизи поверхности Земли пренебрежимо мало по сравнению с силой притяжения к центру Земли. При удалении точки от поверхности Земли сила притяжения к центру Земли будет уменьшаться, и пренебрегать влиянием притяжения Солнца уже будет нельзя. На достаточно большом расстоянии от поверхности Земли влияние силы притяжения со стороны Земли станет незначительным по сравнению с силой притяжения к Солнцу. При вычислении орбиты нужно принимать во внимание это обстоятельство и, пренебрегая притяжением Земли, рассматривать движение в центральном силовом поле Солнца.
Чтобы определить скорость, которую необходимо сообщить точке для ее движения по параболической орбите относительно Солнца, можно снова воспользоваться интегралом живых сил, в котором следует принять значение 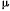для Солнца. Не приводя здесь
всех расчетов, скажем, что для движения по параболической орбите необходимо сообщить точке скорость около 42,2 км/сеч (относительно системы осей, связанных с Солнцем и ориентированной по звездам). Начав движение с такой начальной скоростью, точка будет двигаться но параболической орбите относительно Солнца и навсегда покинет Солнечную систему. При определении начальной скорости точки относительно Земли необходимо учитывать движение Земли по своей орбите во время удаления точки от Земли и притяжение со стороны Земли, пока точка находится в сфере ее действия. Поэтому скорость точки относительно Земли должна быть около 16,7 км!сек. Эта скорость называется третьей космической скоростью.
Эллиптическое движение точки. Рассмотрим подробно случай, когда постоянная живых сил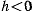 
и точка совершает движение по эллиптической орбите с фокусом в 
.
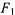Фокальное уравнение эллипса имеет вид
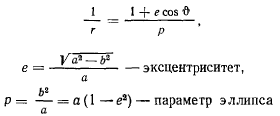
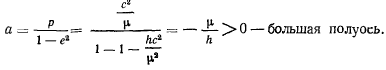
Предположим, что в начальный момент точка находится в положении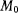 
и имеет начальную скорость 
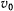. Тогда величина большой полуоси
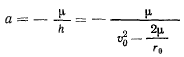
будет неизменной вне зависимости от направления начальной скорости точки. Для определения орбиты достаточно найти положение второго фокуса, которое можно определить из условия, что сумма расстояний от точки траектории до фокусов есть величина постоянная, т. е.
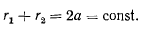
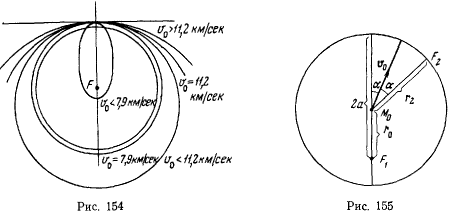
Пусть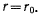 
Геометрическое место фокусов представляет собой окружность радиуса
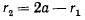
с центром в точке 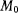(рис. 155). Известно, что касательная к эллипсу делит пополам угол между фокальными радиусами. Следовательно, зная направление начальной скорости точки, можно определить положение второго фокуса 
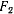. Этим полностью решается задача определения траектории. Для ее выполнения, оказывается, достаточно знать величину и направление начальной скорости и начальное положение материальной точки.
Задача попадания. Рассмотрим задачу о том, в каком направлении следует запустить из данного положения материальную точку с начальной скоростью чтобы она, двигаясь в центральном силовом поле, попала в наперед заданную точку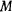 
.
При решении этой задачи заметим, что на материальную точку действует центральная сила притяжения, величина которой обратно пропорциональна квадрату расстояния точки от притягивающего центра, являющегося одним из фокусов 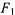эллиптической орбиты. Определив, как это указывалось выше, большую полуось орбиты 
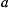и зная 
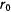, найдем геометрическое место вторых фокусов эллиптических траекторий, являющееся окружностью радиуса
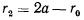
с центром в точке 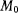. Точка 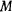должна лежать на искомой траектории, т. е. должно удовлетворяться уравнение
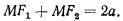
Построив окружность радиуса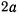 
с центром в фокусе 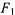из точки 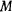опишем окружность радиуса
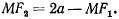
Эта окружность будет геометрическим местом вторых фокусов траектории (рис. 156). Пересечение двух окружностей определит второй фокус (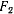
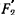или 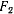на рисунке).
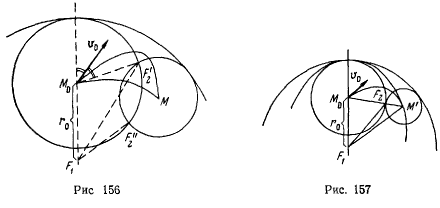
Две окружности либо пересекаются в двух точках, либо касаются друг друга, либо вообще не имеют общих точек. В последнем случае попадание в точку 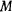из положения 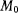при данной начальной скорости невозможно. Если имеются два фокуса, то попадание возможно двумя способами.
Определим геометрическое место точек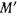 
, в которые можно попасть только одним способом, т. е. когда существует только один второй фокус. Для этого случая имеем
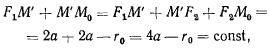
и точки 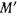расположены на эллипсе, фокусами которого являются точк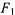и и 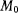(рис. 157). В точки, расположенные на этом эллипсе, можно попасть только одним способом; в точки, лежащие за пределами эллипса, попасть при заданной начальной скорости нельзя.
По аналогии с параболой безопасности (см. задачу о движении тяжелой точки в пустоте), полученный эллипс будем называть эллипсом безопасности. Для определения начальной скорости достаточно разделить пополам угол, образованный прямым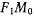и 
и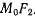 
.
Пример:
Определить наименьшую скорость, с которой из положения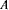 
земной поверхности нужно бросить снаряд, чтобы попасть в точку 
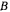Земли (рис. 158)
Решение:
По условиям задачи, попадание должно осуществляться на предельном режиме, т. е. когда точка 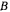будет расположена на эллипсе безопасности, фокусами которого являются точк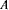и и 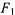. Второй фокус расположен на середине отрезка 
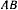, Зная фокус 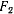можно построить траекторию, которая должна быть расположена вне Земли. Направление начальной скорости определяется из условия, что вектор скорости делит пополам внешний угол между фокальными радиусами. Величина начальной скорости находится из интеграла живых сил
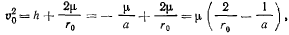
где
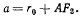
в) Определение времени в эллиптическом движении планет.
Во многих задачах небесной механики необходимо знать время движения точки (планеты) по эллиптической орбите. Рассмотрим движение планеты относительно Солнца в системе осей, имеющих начало в центре Солнца и сохраняющих неизменное направление относительно звезд. Уравнение траектории планеты запишем в полярной системе координат
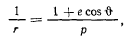
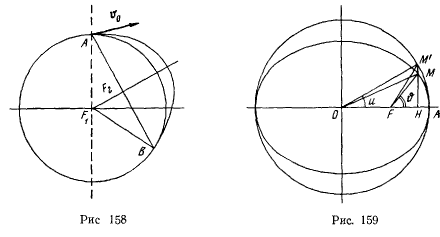
где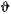 
— угол между большой полуосью орбиты и радиус-вектором планеты, называемый истинной аномалией. Вершину орбиты, ближайшую к Солнцу, называют перигелием, а более удаленную — афелием. Эллиптическую траекторию можно рассматривать как проекцию описанного круга, который нужно повернуть вокруг большой полуоси на угол, косинус которого равен 
.
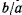Пусть 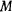— точка (планета) на эллиптической орбите, а 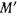— соответствующая точка описанного круга (рис. 159). Угол 
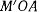называют эксцентрической аномалией планеты.
Выразим время движения планеты через эксцентрическую аномалию. Из построения эллипса имеем
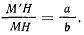
Рассмотрим площадь сектора
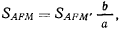
но
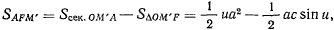
где
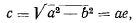
так что
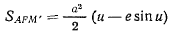
и
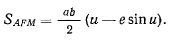
Движение планеты по орбите происходит по закону площадей, т. е. площади, описываемые радиус-вектором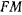 
, пропорциональны времени движения. Тогда
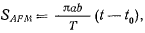
где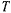 
— период обращения планеты; 
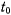— время прохождения через перигелий. Сравнивая два последних соотношения, получим
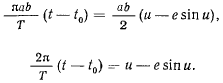
Полученное уравнение выражает время движения планеты через эксцентрическую аномалию. Полагая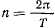 
придем к уравнению Кеплера
Для завершения задачи остается установить геометрическую зависимость между истинной и эксцентрической аномалией.
Перепишем уравнение эллипса в виде
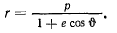
Подставляя сюда значение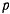 
, выраженное через эксцентриситет 
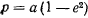, получим
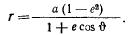
С другой стороны, вводя прямоугольную систему координат с началом в центре эллипса, перепишем уравнение эллипса в виде
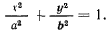
Тогда
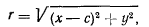
что преобразуется к виду
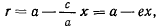
где
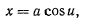
отсюда получаем
Сравнивая два значения для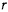 
, будем иметь
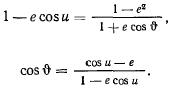
Полученная формула легко преобразуется к виду, удобному для логарифмирования. В самом деле, подставляя в формулу
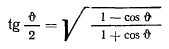
значение для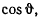 
, получим
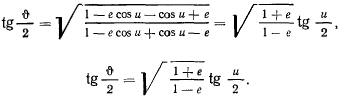
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Основные теоремы динамики для свободной материальной точки |
| Движение тяжелой материальной точки в пустоте |
| Движение точки в сопротивляющейся среде |
| Движение несвободной материальной точки |
