Оглавление:
Движение материальной точки под действием центральной силы. Закон площадей
Центральной силой называется сила, линия действия которой все время проходит через один и тот же неподвижный центр. С силами такого рода приходится встречаться при рассмотрении задач небесной механики (движение планет в поле тяготения Солнца или спутника в поле тяготения Земли), при изучении движения электронов и др.
Очевидно, что для центральной силы
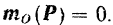
Но тогда, как это следует из уравнения (171), во все время движения материальной точки, на которую действует центральная сила, момент количества движения этой точки есть величина постоянная. По свойству векторного произведения вектор
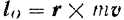
перпендикулярен к плоскости, образованной векторами 
и 
, и потому радиус-вектор 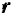точки и ее скорость 
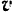должны во асе время движения точки лежать в одной плоскости.
Модуль количества движения точки (рис. 193):
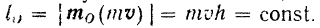
Массу точки мы рассматриваем как величину постоянную. Следовательно, при действии на нее центральной силы будем иметь
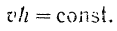
Последнему результату можно дать и геометрическое истолкование. Пусть за время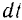 
точка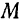 
сместилась на элемент дуги
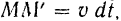
а радиус-вектор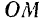 
описал сектор, заштрихованный на рис. 193. Площадь этого сектора
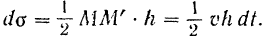
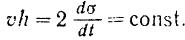
Величина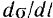 
, характеризующая быстроту изменения во времени площади, ометаемой радиусом-вектором 
движущейся материальной точки, называется секторной скоростью этой точки.
Из сказанного вытекает следующий вывод: под действием центральной силы материальная точка движется по плоской кривой с постоянной секторной скоростью и, следовательно, за равные промежутки времени радиус-вектор этой точки ометает равные площади. Данный закон был открыт И. Кеплером (1571 — 1630) и носит название закона площадей.
Пример задачи:
Искусственный спутник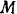 
Земли движется по эллипсу с эксцентриситетом 
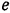, под действием силы 
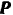притяжении к центру Земли, находящемуся в одном из фокусов 
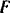эллипса (рис. 194). Определить скорость 
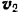спутника в наиболее удаленной от фокуса точке 
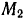(называемой афелием), если его скорость в наиболее близкой к фокусу точке 
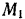(называемой перигелием) равна 
.
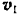Решение:
Примем спутник 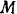(рис. 194) за материальную точку. Так как на нее действует центральная сила, то модуль момента количества движения этой точки относительно центра силы есть величина постоянная:
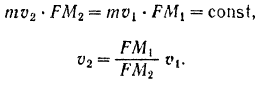
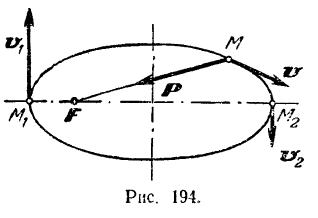
Как известно из аналитической геометрии, эксцентриситет эллипса 
, где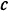 
— расстояние от центра эллипса до фокуса и 
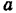— большая полуось эллипса. Отсюда находим:
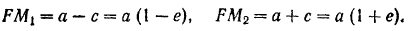
Таким образом, искомая скорость спутника
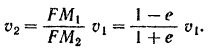
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
