




- Принимая во внимание случай очень малого числа Рейнольдсовских движений, мы переходим к очень большому числу Рейнольдсовских движений в противоположной крайности, то есть когда сила инерции преобладает над силой вязкости. Установите вязкость уравнения Навье-Стокса на ноль и получите уравнение движения идеальной (или невязкой) жидкости. Эти уравнения называются уравнениями Эйлера. (12. Тридцать семь) (12.38) 12.
Тридцать девять. Теория идеальной жидкости используется в аэродинамике, особенно при расчете подъемной силы профиля крыла. Эта теория также используется в общих задачах обтекания объекта, так как она определяет распределение давления на внешней границе пограничного слоя. Поскольку эта теория предполагает нулевую вязкость, она вызывает проскальзывание на твердом теле surface. As упомянутый ранее(гл.8), фактически отсутствует скольжение по поверхности, а в пограничном слое вблизи поверхности необходимо учитывать эффекты вязкой и сдвиговой деформации. Однако для потоков, которые удаляются от тела, часто применяется предположение об идеальности жидкости.
Идеальная кинетической теории жидкости наиболее широко используются инженерами авиации. Однако она играет важную роль в изучении механики жидкости инженерами всех специальностей. Дальнейшее обсуждение будет ограничено простым случаем отсутствия вихря или потенциального потока. Это название означает, что в жидкости нет вращения или вихря. Потенциальный ток Понятие потенциала широко известно. Появились воспоминания и представления о потенциальной энергии гравитационного поля. Если ось 2 направлена вертикально вверх, то массовая сила 2 =- # (м / с2).Потому что изменение потенциальной энергии&равно работе, выполняемой при перемещении массы 1 кг и направлении оси 2 = 2dg И 12.
Сорок (12.41) где сила представлена в виде градиента потенциала. Определите потенциал скорости φ (x, y) по аналогии (ограничив его для простоты 2-D потоком) так, чтобы скорость была равна наклону потенциала. Так… (12.42) II (12. Сорок три) Подставляя эти уравнения для скорости Рябь. Диу «ЦОР * делать» (12.44) E2f, d2f n dx2 1 du2″(12. Сорок пять) — уравнение Лапласа. Если мы знаем соответствующие начальные и графеновые условия, мы можем найти φ (x, y), решая это уравнение. Тогда формула(12. 42) и (12. 43)из любой точки вы можете получить скорость.
Однако до сих пор мы просто предполагали, что существует потенциальная функция φ (x, y), но на самом деле она существует только в том случае, если поток удовлетворяет определенным требованиям. Уравнение (12. 42) и (12. 43) дифференцируя Дих_______________________ d2 (p ду ду ДХ. 5 и u _ d2f dhdhdu ’ (12. Сорок шесть) (12. Сорок семь) Поскольку функция φ (x, y) уникальна, и все ее 2-е производные, как полагают, существуют в x, правые части этих уравнений конгруэнтны、 ^-> = 0.
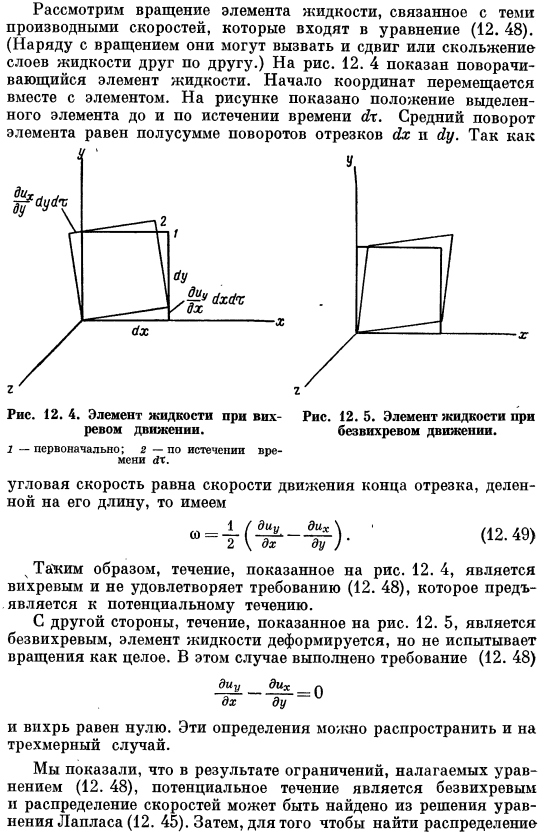
Формула (12. 48) сумма на левой стороне называется vortex. As описанный ниже угол поворота текучего элемента относительно оси, параллельной оси 2, равен 2-кратной скорости вращения. Уравнение (12. 48) рассмотрим вращение текучих элементов, связанных с производной скорости, содержащейся в. (Помимо вращения, они могут вызывать сдвиг или скольжение слоя жидкости друг вдоль друга. 12. 4 показан вращающийся жидкий элемент. Начало координат перемещается вместе с элементом. На рисунке показано положение выбранного элемента до и после НХ. Среднее вращение элементов равно полупроницаемой сумме вращений сегментов Hx и Well. С РО звук движения. Не вращательное движение. 1-первый; 2-после Ах.
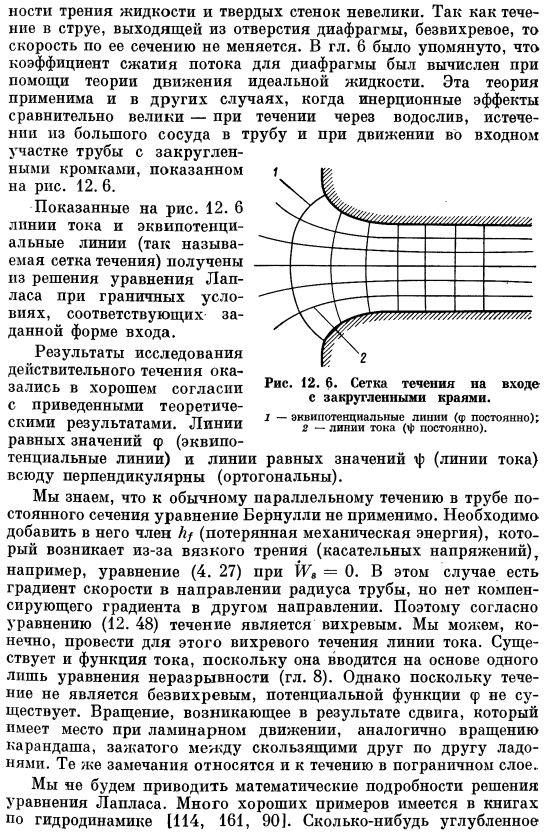
- Если угловая скорость равна скорости конца отрезка, деленной на его длину. Таким образом, поток, показанный на рисунке, равен 12. 4-вихрь, а также требования, предъявляемые к потенциальным утечкам (12. 48)не встречается. Между тем, поток показан на рисунке 12. 5 является невращающимся, текучий элемент деформируется, но не вращается как whole. In в данном случае требования (12. 48) будет взиматься плата. Ди У Диг _ Н ДХ ду И вихрь равен нулю.
Эти определения могут быть расширены до трехмерных случаев. Формула (12. 48) в результате ограничений, налагаемых потенциальным потоком, происходит невращение, а распределение скоростей зависит от уравнения Лапласа(12. 45) показал, что его можно определить из решения. Затем вы можете использовать уравнения Эйлера, чтобы найти распределение давления. Для двумерного стационарного вихревого течения несжимаемой жидкости формула(12. 46) и Формула (12. 37) формула, записанная на оси x(12. 41) и подставляя、 Это уравнение может быть получено путем интегрирования ±(У1 + 4) — а + — * ■ = / > М.(12.51)) Аналогично уравнению(12. Тридцать восемь) ±(α1+ 4) th + — > = / 2 (ar).
Левая часть этих уравнений равна / x (y)= / 2(x)= C0P81. Следующий + =(12.53) Так что у нас есть — =const1(12.54) 2/2 — уравнение Бернулли. Вы можете описать 2 точки потока по-разному. 4._ да + * ₽ = 0. (12.55) И Из Формулы (12.41) =(12.56) Тогда получим уравнение ^-+ 4-D2 + — = 0, (12.57) Формула(4. 21) также. (Последний содержит b вместо and, но индекс на самом деле не нужен, потому что, по предыдущему предположению, невозможно изменить скорость вдоль входных и выходных секций.) В этом случае вихревой поток и u b совпадают.
Помните, что в разделе 6, используя уравнение Бернулли, мы исследовали поток между трубкой Пито и диафрагмой расходомера и сечение сжатия выходного отверстия flow. It нетрудно заметить, что в этих устройствах инерционная сила фактически преобладает над вязкой. Ускорение потока вызвано изменением площади поперечного сечения. 12. 6. An сетка подачи входа с округленными краями. I-эквипотенциальная линия (всегда; всегда 2 линии тока) Трение между стенками жидкости и твердого тела невелико.
Поток струи, выходящей из отверстия, не вращается, поэтому скорость вдоль его поперечного сечения не изменяется.6 из вас упомянули, что степень сжатия потока диафрагмы рассчитывается с использованием теории движения идеальной жидкости. Эта теория также может быть применена в других случаях, когда инерционный эффект относительно велик-12.6, если он течет через водосброс, если он проливается в трубу из большого контейнера, и если край перемещается круглым входом трубы, как показано на рисунке. Рисунок 12. 6 обтекаемые и эквипотенциальные линии (так называемая Сетка течения) получены из решения уравнения Лапласа при граничных условиях, соответствующих заданной входной форме.
Результаты исследования фактического течения хорошо согласуются с теоретическими результатами. Равные линии Р (экипо Линия (линия потока) равного значения 潜在的 (потенциальная линия) является вертикальной (ортогональной) везде. Известно, что уравнение Бурпулли неприменимо к нормальным параллельным течениям в трубе с постоянным поперечным сечением area. To к этому надо добавить L /(потерянную механическую энергию).Это вызвано вязким трением (тангенциальным напряжением).Например, уравнение W = 0 (4.27). в этом случае существует градиент скорости в радиальном направлении трубы. Однако, нет никакого градиента коррекции в другом направлении. Отсюда и Формула 12.
По течению представляет собой вихрь. Конечно, вы можете нарисовать линию потока этого водоворота. Существует также функция потока, поскольку она вводится только на основе уравнения непрерывности (Глава 8).Однако в потоке нет вихря, поэтому нет потенциальной функции p. вращения, возникающие из сдвигов, которые происходят во время ламинарного движения, напоминают вращения карандаша, зажатые между ладонями, которые скользят друг против друга. То же самое относится и к течению пограничного слоя. Математические подробности решения уравнения Лапласа не приводятся.
Смотрите также:
| Ламинарное движение в круглой трубе | Течение в пограничном слое |
| Ламинарное движение в кольцевом зазоре | Сопротивление при обтекании плоской пластинки |
