Оглавление:



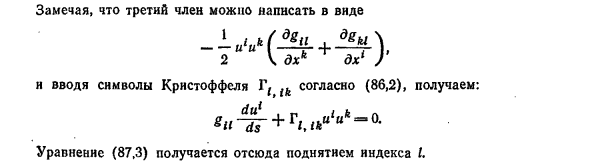

Движение частицы в гравитационном поле
- Движение частиц в гравитационном поле. Специальное движение свободных частиц Относительность определяется по принципу минимума Действие: „ SS = -Tsb / ds = 0, (87,1) Частицы движутся таким образом и мир Ния — крайность между двумя мирами Точки, в данном случае прямые (нормальное 3D Это пространство, соответствующее прямой униформе Движение).
Движение частиц в гравитационном поле должно быть определено Принцип минимального действия в том же формате (87.1) Потому что гравитационное поле — это просто изменение. Метрика пространства-времени, которая проявляет себя Измените dx1 из выражения ds.
частицы движутся, чтобы указать на мир Перейти к крайностям или Людмила Фирмаль
Так гравий Поле станции, , как говорится, геодезии 4 пробела x0, x 1 x2, x3 строки, однако При наличии пространственно-временных негативов Слева эта линия не является «прямой линией» Движение частиц не является ни равномерным, ни линейным.
Движение частиц в гравитационном поле331 Вместо того, чтобы прямо из пудинга Шифр минимального действия (см. Задачу в этом параграфе), Упростите поиск уравнений движения для гравитационных частиц Соответствующее поле путем обобщения производной Уравнение свободного движения частиц в специальной теории.
- Теория относительности, то есть система четырех координат Галилея. эти Уравнение говорит, что dul jds = 0 или dul = 0. Где u1 = dx1 / ds Есть четыре скорости. Ясно в криволинейных координатах Это уравнение Du * = 0. (87,2) Из уравнения для ковариантного дифференцирования векторов (85.6) У нас есть DV? + Tlklukdxl = 0. Разделив это уравнение на дс d2xl -p ^ dx1 dx1 _ DS2 DS DS Это желаемые уравнения движения.
Мы видим это Время жизни частиц в гравитационном поле зависит от величины Thc1. Производная d2xl / ds2 представляет собой четырехчастичное ускорение. так Объем можно назвать tTrk1iki1 «4-сила», действующий Частицы гравитационного поля. тензор Роль «потенциала» гравитационного поля — его производной Определить «напряженность» поля Tgk1g).
могут быть обнулены в любое время Заданная точка в пространстве-времени Людмила Фирмаль
§ 85 показал выбор соответствующей системы Все Th1 . в настоящее время Выбор такой локальной инерциальной системы отсчета Устранение этого бесконечно малого гравитационного поля Элемент пространства-времени и возможность такого выбора являются представлением принципа эквивалентности в относительности Теория гравитации 1).
Четырехмерный импульс частиц в гравитационном поле Определяется как pg = m si \ (87,4) И квадрат p {pr = m 2s2. (87.5) Если вы используете d S / d x 1 вместо -pi, чтобы заменить здесь, уравнение Ha Милтон Якоби частиц в гравитационном поле: gik ^ ^ -m 2c2 = 0. (87,6) 6 дх1 дхк в ‘ Для распространения оптических сигналов, геодезических уравнений (87.3) строки формата не применимы.
Линия распространения луча, расстояние ds = 0 и Все члены в уравнении (87.3) бесконечны. для Придайте желаемую форму уравнению движения в этом случае У нас есть направление распространения света В геометрической оптике он определяется волновым вектором Выдающийся в луче.
Таким образом, вы можете написать четыре измерения волновой вектор вида kg = dx1 j d \ Метр, который изменяется вдоль луча. В специальной теории Распространение света в вакууме, волновой вектор Не изменяется вдоль луча, т.е. dkl = 0 (см. §53). Гравитацией Поле, где это уравнение становится D kl = 0, или ^ — + кk1kkk1 = O (87,7) (Параметр A также определяется из того же уравнения) 2).
Квадрат вектора 4 волны равен нулю (см. § 48). Кик {= 0. (87,8) Если вы замените здесь df / dxr вместо k {(f-eikonal), уравнение будет найдено. Эйконал в гравитационном поле: gk df d ± = 0_ (879) 6 дх1 дхк у ’ Релятивистские уравнения в низкоскоростном предельном случае Движение частиц в гравитационном поле должно двигаться Положите te в соответствующее нерелятивистское уравнение.
В то же время Из предположения, что скорость мала Кроме того, само гравитационное поле В противном случае частицы в нем Вы можете получить большую скорость. Давайте рассмотрим, как метрики связаны в этом ограничительном случае. Тензор Гик <р гравитации с нерелятивистским потенциалом Поле.
В нерелятивистской механике движение гравийных частиц Поле станции определяется функцией Лагранжа (81.1). мы Написать в следующем формате L = -mc2 + ™ —- m <p, (87.10) Добавьте константу — mc2 г). Сделать это Нерелятивистская функция Лагранжа L = без поля = -mc2 + m v2 / 2 было именно то, что он вошел Соответствующая релятивистская функция L = -mc2 y / 1-v2 / c2 С такими ограничениями, как v / c- »0.
Нерелятивистское действие S на гравитационные частицы Следовательно, формат поля S = J L dt — mc J + -) dt. Сравните это с уравнением S = —mc f ds Рассмотрен ограниченный случай дс = (с — ч дт. \ 2 с) Удалить круговые термины, возводя их в квадрат До нуля находим ds2 = (c2 + 2 (f) dt2-dr2 (87.11)
Здесь мы рассмотрели v dt = dr. Следовательно, липкая компонента преметрического тензора Случай равен goo = 1 + h- (87,12) (87.11) для остальных компонентов Разрыв = 5AR, Гоа = 0. Однако на практике Вообще говоря, модификации того же размера, что и те, исправление (см. * ° для деталей на §106).
невозможно Определение этих модификаций вышеуказанным способом является актуальным Поскольку поправка для ga / # имеет одинаковый размер, Станьте участником функции Лагранжа в качестве исправления Чем меньше высший порядок (в формуле Для ds2 компонент разрыва не умножается на c2. липкое место) — Оспаривать
Выведите уравнение движения (87.3) из принципа минимального движения Wii (87,1). Решения. У нас есть Sds2 = 2 dsSds = S (gikdxldxk) = dxldxk ^^ — Sxl + 2 gikdx1 d8xk. дх так д. i x k igd xd 1xd 1 / f c xdx1 dSxkx1 dSx \ S (e.i.-j-) Sxk ^ ds dxg dxk dgik r i d / dxg дс дс дх1 дс \ лк дс (При интеграции в части мы считали, что 5xx = 0 или меньше). второй В терминах ниже интеграла замените индекс на индекс I.
Любой коэффициент вариации 5х1, 1 г до джик д, их 1 я до джик дл и я кдгил н Обратите внимание, что третий термин может быть записан как Согласно (86.2), вводя символ Кристоффеля Г ^, du, «r» r to __ l Gil ‘+ ^ l, iKU U-0 * Д.С. Уравнение (87.3) можно получить, увеличив индекс I.
Смотрите также:
| Ковариантное дифференцирование | Постоянное гравитационное поле |
| Связь символов Кристоффеля с метрическим тензором | Вращение в физике |

