Оглавление:


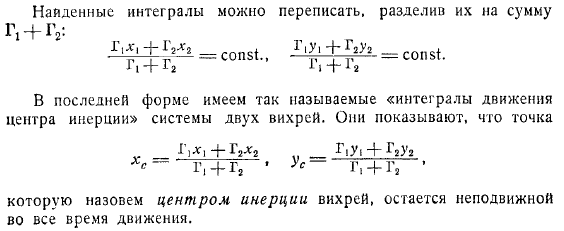

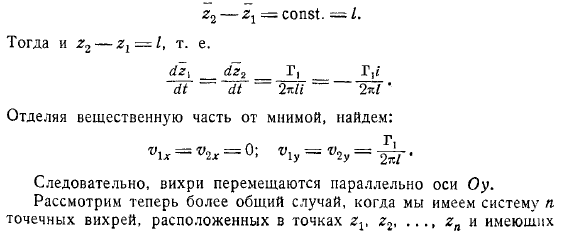



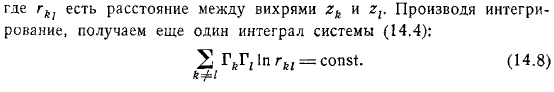

Две прямолинейные вихревые нити. Движение системы вихрей
Есть параллельных прямых вихря. В предыдущем случае можно рассмотреть движение в плоскости, перпендикулярной нити. Возьмем эту плоскость за плоскость комплексной переменной. Интенсивность гидромеханики точечного вихря получается на пересечении плоскости и нити накала. Комплексный потенциал равен сумме потенциалов, соответствующих каждому вихрю, то есть комплексной скорости. Потому что вы можете написать следующее дифференциальное уравнение.
Изучите движение вихрей в жидкости. Другой вихрь не движется, поэтому вихрь одной точки движется только под влиянием другой (сам вихрь не работает). Так же, как вихрь вращается вокруг первого, первый вихрь вращается вокруг по окружности, и расстояние между вихрями остается постоянным в течение всего. To докажите эти наиболее очевидные утверждения, Эдди создает дифференциальное уравнение. To получить скорость первого вихря, в выражении комплексной скорости, отбросить первый член и поместить его во.
- Аналогичным образом, разделяя действительную и мнимую части этих уравнений, мы приходим к следующей системе дифференциальных уравнений: сначала умножаем первое уравнение на, затем умножаем, а затем умножаем уравнение на и добавляем следующее. Здесь мы находим интеграл от суммы интегралов. в последнем виде существует так называемый «Интеграл движения центра инерции» системы из вихрей. Они показывают прямолинейность вихревая нить , что точка, которую они называют инерционным центром вихря, остается неподвижной в течение всего движения.
Затем преобразуем систему уравнений следующим образом: вычитаем из первого уравнения и вычитаем. Умножьте первое из этих уравнений на и второе на. Если проинтегрировать это уравнение, то оно выглядит так: если сравнить этот результат с предыдущими результатами по сохранению центра инерции вихря, то получится, что вихря вращаются вокруг центра инерции при сохранении расстояния между ними.
В теории сверхпроводимости вихрями Абрикосова называют вихри сверхтока в сверхпроводниках второго рода. Людмила Фирмаль
В частном случае, то есть когда вихрь находится в обратном вращении с одинаковой интенсивностью, центр инерции находится на Бесконечности, так как знаменатель. Покажем, что вихрь движется вперед с постоянной скоростью, перпендикулярно прямой, соединяющей вихри. На самом деле вихри первых моментов находятся на оси на расстоянии друг от друга.
Затем из уравнения движения в виде: далее, разделяя действительную и мнимую части, мы можем видеть следующее. Таким образом, вихрь движется параллельно оси. Где точка если существует система точечных вихрей, которые расположены в и имеют силу, рассмотрим более общую. В этом случае комплексный потенциал имеет вид: если это комплексная скорость, то мы получаем выражение.
- Движение вихря определяется уравнением из этих уравнений нетрудно угадать несколько простых результатов. Если мы умножим уравнение системы на и сумму, то легко увидим, что все члены справа отменяют друг друга. Для можно переписать полученный интеграл в виде: «Интеграл движения центра инерции»: аналогично, умножая уравнения системы и суммирования значок от до, равенство и мнимую части, находим: из этих нитей уравнений равенства — суммарный импульс круговой вихревой нити потоков массового происхождения.
М время. Первое выражение этих уравнений можно переписать так, то есть сумма массового момента инерции относительно начала координат не изменяется со временем. Наконец, умножив уравнение системы на, мы достигаем равенства, разделяющего мнимую часть: где расстояние между вихрями. Интегрируйте, чтобы получить еще один интеграл системы.
Сверхток циркулирует вокруг нормального (несверхпроводящего) домена, представляющего собой цилиндр, вытянутый вдоль направления внешнего магнитного поля, образуя вихрь. Людмила Фирмаль

