Оглавление:






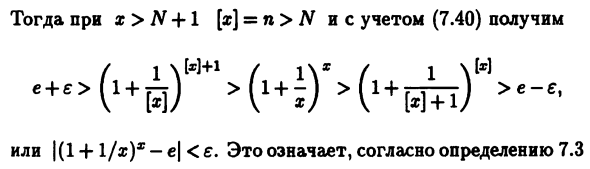




Два замечательных предела
- Рассмотрены свойства функций, которые имеют ограничения на определенные точки Добавочная линия € R, дайте возможность Проанализируйте их поведение вблизи этой точки. Тем не менее, Многие случаи этих свойств и установленных правил для ограничений Одной миграции недостаточно. Один из классических примеров Это поведение функции (sinx) / x вблизи точки а = 0. х — центральный угол или длина дуги Радиус единицы (рис. 7.12) и 0 тг / 2 (7,34) Очевидно, неравенство | sinx | <1. (7.34) Но Функция.
Поэтому (7.34) также применимо к x <0. (7.34) x = 0 равно. Сразу после (7.34) limsin £ = 0 и limcosx = l. (7,35) Фактически из-за неравенства | sinx-0 | ^ | x | и | cosx-l | = = 2sin2 (x / 2) ^ s2 / 2 в (7.3), достаточно установить 8 = e (7.35) доказательство первого предела и 6 = y / 2e Второе доказательство. Вернемся к двойному неравенству. С его левой стороны Если x € (0, м / 2) (atx) / x <1, следуйте этому Поскольку (sinx) / z равно x∈ (-tr / 2, 0), неравенство также верно. Четная функция. С правой стороны двойного неравенства В случае х € (0, п / 2) он становится совой. <(Сина;) / а: Это неравенство
Это также верно из-за соотношения функций, включенных в него x∈ (−π / 2, 0). так coss <- <1 Ва; € (-, -) \ {0}, Людмила Фирмаль
Другими словами, функция (sinx) / x окружена двумя функциями. x- * 0 имеет те же ограничения, что и 1. Таким образом, Согласно утверждению 7.1, мы получаем lim- = 1 (7,36) Называется первый заметный лимит. Геометрический смысл (7.36) Уменьшите центральный угол x длины (см. Рис. 7.12) Секторные дуги и их связки вместе. Используйте (7.36) В противном случае можно рассчитать пределы Можно рассчитать только на основе ранее полученных результатов Для появления под знаками так называемого предела Тип 0/0 неопределенности. Пример 7.12 а. Для (7.23), (7.24), (7.35) и (7.36) Мы получаем (7,37) = лимф) = L x x- ¥ 0 \ x cosxj lim cosa? 1 б. Учитывая (7.4), (7.23), (7.33) и (7.36) ,. sin5z .. 5sin5x lim = lim- * th x x- * о эх о грешный = 5 lim- = 5-1 = 5. V-40 U с.
Учитывая (7.4), (7.23), (7.33) и (7.36) ободок грех2 за; 9sm23a: х- * о 9х * Y = 3 г у-> о х-> 0 = 91im в Рассчитать, используя (7.4), (7.23), (7.24), (7.33) и (7.36) .. sin5s Rim. 0 8 .. / sin5x bx bx \ = lim I-r-1 = x- ¥ 0 ¥ bx bx 81n bx) \ м грех 5а Bx 5 ^ с г ободок х- * 0 ОН Проверьте на равенство сейчас ободок lim (1 + -) = e, (7,38) Называется второй великий предел. х> 1 1 <[x] <* <[«] +1, (7,39) Где M — целая часть числового значения x (см. 3.2) или 4 После лечения 1 • 1 ^ ^ r ~~ T ^ • * ■ • х] +1 х [х] Отсюда 1 + GTT7 <1 + — <1 + GT Все части этого неравенства больше единицы.
- Так позже Повысить эти показатели в положительную сторону Соответствующая часть неравенства (7.39) / 1 \ (6.26) Согласно NЭn— ► ° ° lim {(l + l / n) n} = e. тогда Рассмотрим (6.11) и (6.12) (см. Теорему 6.4 для арифметики) Действие для сходимости последовательности) n + 1 и = Оправа h 1 v + 1i 1+ е (6.7) (см. Определение ограничения 6.3) Последовательность) Для любого e> 0, поскольку существует N∈N, Если n> N n + 1 и -e Тогда, если x> N + l [x] = n> N, учитывая (7.40) H Или | (14-1 / a;) * -e | <e. То есть согласно определению 7.3.
Давайте оо. х = -и х-у Ооо и … Получить после того же преобразования Согласно (7.33), выполнить изменения переменных и принять во внимание (7.23) (7.41) найти ободок -) = Lim (1 + -C-) • lim (l + -l-) = e.l = e. XJ u-H-oo \ U-1 / u- ^ + oo \ tt-1 / В результате любым способом искать х бесконечно верно (7.38). Функция y = 1 / x (7,14) -b.m. X- »oo, т.е. у-> 0. В результате (7.38), изменение переменной согласно (7.33) При условии, что УФ-излучение (7,42) На первый взгляд результат (7.42) (и (7.38)) Парадоксально: если y- * 0 1 + y-> 1 и любая единица Unit!
Ограничения на функции в качестве аргументов имеют тенденцию быть + oo. ободок YAG-Ts-OO -1 = е. х) (7,41) х — »- Людмила Фирмаль
Но индекс 1 / у y-> 0 — функция bb, и пока нет никаких оснований для получения степени Единица, отличная в БМ, но если у ^ + 0 Функция (см. 7.5), предел больше 1. Изменить значение Функция g (y) = (l + y) 1 ^ y уменьшается, как показано ниже (Помните, что приблизительное значение было дано в c.v. е «2,71828). в Я (U) 1 2 1/2 2250 1/3 2370 1/4 2441 О.Д. 2594 0,01 2,7047 0,001 2,7169 0,0001 2.7181 В сущности, (7.38) и (7.42), как говорится, Обложки «Тип 1 ° Неопределенность». Пример 7.13 Расчет функционального лимита Как и x- ¥ оо, этот тип неопределенности таков: После того же преобразования Введите 1 / x2 = y и -2 / x2 = r. Для x-> oo оба y-> 0 и z- * 0, поэтому после замены Переменные с учетом (7.33), (7.23) и (7.42) ободок
Смотрите также:
| Предел функции в точке | Экспонента, натуральные логарифмы и гиперболические функции |
| Предел сложной функции | Понятие предела отображения |

